機器學習入門核心算法:GBDT(Gradient Boosting Decision Tree)
- 1. 算法邏輯
- 2. 算法原理與數學推導
- 2.1 目標函數
- 2.2 負梯度計算
- 2.3 決策樹擬合
- 2.4 葉子權重計算
- 2.5 模型更新
- 3. 模型評估
- 評估指標
- 防止過擬合
- 4. 應用案例
- 4.1 金融風控
- 4.2 推薦系統
- 4.3 計算機視覺
- 5. 面試題及答案
- 6. 優缺點分析
- 優點
- 缺點
- 7. 數學推導示例(回歸問題)
1. 算法邏輯
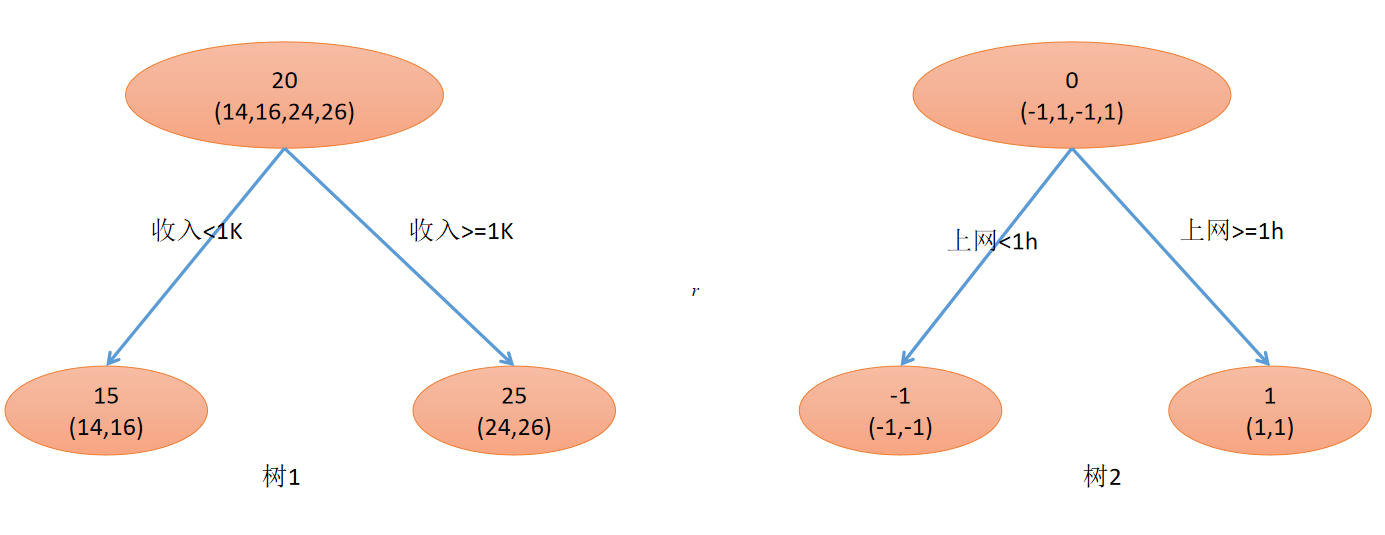
GBDT 是一種基于決策樹的集成學習算法,屬于 Boosting 家族。其核心思想是串行訓練多個弱學習器(決策樹),每棵樹學習前序模型殘差的負梯度,最終通過加權求和得到強學習器。核心邏輯如下:
- 初始化:用常數值初始化模型(如目標均值)
F 0 ( x ) = arg ? min ? γ ∑ i = 1 n L ( y i , γ ) F_0(x) = \arg\min_\gamma \sum_{i=1}^n L(y_i, \gamma) F0?(x)=argγmin?i=1∑n?L(yi?,γ) - 迭代訓練:
- 計算當前模型的偽殘差(負梯度)
- 訓練新樹擬合該殘差
- 更新模型: F m ( x ) = F m ? 1 ( x ) + ν h m ( x ) F_m(x) = F_{m-1}(x) + \nu h_m(x) Fm?(x)=Fm?1?(x)+νhm?(x)( ν \nu ν為學習率)
- 最終輸出:加權樹組合
F ( x ) = ∑ m = 0 M ν h m ( x ) F(x) = \sum_{m=0}^M \nu h_m(x) F(x)=m=0∑M?νhm?(x)
2. 算法原理與數學推導
2.1 目標函數
設訓練集 { ( x i , y i ) } i = 1 n \{(x_i,y_i)\}_{i=1}^n {(xi?,yi?)}i=1n?,損失函數 L ( y , F ( x ) ) L(y, F(x)) L(y,F(x)),目標是最小化正則化目標函數:
L = ∑ i = 1 n L ( y i , F ( x i ) ) + ∑ m = 1 M Ω ( h m ) \mathcal{L} = \sum_{i=1}^n L(y_i, F(x_i)) + \sum_{m=1}^M \Omega(h_m) L=i=1∑n?L(yi?,F(xi?))+m=1∑M?Ω(hm?)
其中 Ω ( h m ) = γ T + 1 2 λ ∥ w ∥ 2 \Omega(h_m) = \gamma T + \frac{1}{2}\lambda \|w\|^2 Ω(hm?)=γT+21?λ∥w∥2( T T T為葉子數, w w w為葉子權重)
2.2 負梯度計算
在第 m m m 次迭代,計算偽殘差:
r i m = ? [ ? L ( y i , F ( x i ) ) ? F ( x i ) ] F ( x ) = F m ? 1 ( x ) r_{im} = -\left[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right]_{F(x)=F_{m-1}(x)} rim?=?[?F(xi?)?L(yi?,F(xi?))?]F(x)=Fm?1?(x)?
| 損失函數 | 偽殘差 r i m r_{im} rim? |
|---|---|
| 平方損失 | y i ? F m ? 1 ( x i ) y_i - F_{m-1}(x_i) yi??Fm?1?(xi?) |
| 絕對損失 | sign ( y i ? F m ? 1 ( x i ) ) \text{sign}(y_i - F_{m-1}(x_i)) sign(yi??Fm?1?(xi?)) |
| Huber損失 | 分段函數 |
| 對數損失(分類) | y i ? 1 1 + e ? F m ? 1 ( x i ) y_i - \frac{1}{1+e^{-F_{m-1}(x_i)}} yi??1+e?Fm?1?(xi?)1? |
2.3 決策樹擬合
訓練新樹 h m h_m hm? 擬合偽殘差 { ( x i , r i m ) } \{(x_i, r_{im})\} {(xi?,rim?)},通過遞歸分裂節點:
- 分裂準則:最大化增益(Gain)
Gain = 1 2 [ G L 2 H L + λ + G R 2 H R + λ ? ( G L + G R ) 2 H L + H R + λ ] ? γ \text{Gain} = \frac{1}{2} \left[ \frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L+G_R)^2}{H_L+H_R+\lambda} \right] - \gamma Gain=21?[HL?+λGL2??+HR?+λGR2???HL?+HR?+λ(GL?+GR?)2?]?γ
其中 G = ∑ i ∈ I g i G = \sum_{i \in I} g_i G=∑i∈I?gi?, H = ∑ i ∈ I h i H = \sum_{i \in I} h_i H=∑i∈I?hi?( g i g_i gi?為一階導, h i h_i hi?為二階導)
2.4 葉子權重計算
對葉子節點 j j j,最優權重為:
w j ? = ? ∑ i ∈ I j g i ∑ i ∈ I j h i + λ w_j^* = -\frac{\sum_{i \in I_j} g_i}{\sum_{i \in I_j} h_i + \lambda} wj??=?∑i∈Ij??hi?+λ∑i∈Ij??gi??
2.5 模型更新
F m ( x ) = F m ? 1 ( x ) + ν ∑ j = 1 J w j 1 ( x ∈ R j ) F_m(x) = F_{m-1}(x) + \nu \sum_{j=1}^J w_j \mathbf{1}(x \in R_j) Fm?(x)=Fm?1?(x)+νj=1∑J?wj?1(x∈Rj?)
3. 模型評估
評估指標
| 任務類型 | 常用指標 |
|---|---|
| 回歸 | MSE, MAE, R 2 R^2 R2 |
| 分類 | Accuracy, F1-Score, AUC-ROC |
| 排序 | NDCG, MAP |
防止過擬合
- 早停法:驗證集性能不再提升時停止迭代
- 正則化:通過 γ \gamma γ, λ \lambda λ 控制復雜度
- 子采樣:每次迭代隨機選擇部分樣本或特征
4. 應用案例
4.1 金融風控
- 場景:信用評分卡
- 特征:收入、負債比、交易頻率
- 效果:AUC 提升 12% 對比邏輯回歸
4.2 推薦系統
- 場景:電商點擊率預測
- 特征組合:自動學習“用戶年齡×商品類別”等交叉特征
- 優勢:處理高維稀疏特征優于協同過濾
4.3 計算機視覺
- 場景:圖像語義分割
- 做法:GBDT 處理 CNN 提取的特征向量
- 結果:在 Pascal VOC 上 mIOU 提升 3.2%
5. 面試題及答案
Q1:GBDT 為什么擬合負梯度?
A:通過梯度下降在函數空間優化,負梯度是損失下降最快的方向。
Q2:如何處理分類特征?
A:最佳實踐是使用直方圖算法(如 LightGBM):
- 按特征取值排序
- 根據梯度直方圖尋找最優分裂點
- 復雜度從 O ( # categories ) O(\#\text{categories}) O(#categories) 降至 O ( bin ) O(\text{bin}) O(bin)
Q3:GBDT vs Random Forest?
| 維度 | GBDT | Random Forest |
|---|---|---|
| 基學習器關系 | 串行依賴 | 并行獨立 |
| 偏差-方差 | 低偏差 | 低方差 |
| 過擬合 | 易過擬合(需早停) | 抗過擬合能力強 |
| 數據敏感度 | 需特征縮放 | 無需特征縮放 |
6. 優缺點分析
優點
- 非線性能力強:自動捕捉高階交互特征
- 魯棒性好:對異常值和缺失值不敏感
- 可解釋性:可通過特征重要性分析(累積分裂增益)
Importance j = ∑ splits ( j ) Gain \text{Importance}_j = \sum_{\text{splits}(j)} \text{Gain} Importancej?=splits(j)∑?Gain - 適用廣泛:支持回歸/分類/排序任務
缺點
- 訓練效率低:串行訓練無法并行化(改進:LightGBM 用 leaf-wise 生長)
- 高維稀疏數據:文本數據表現不如神經網絡
- 超參敏感:需精細調參(樹深度、學習率等)
7. 數學推導示例(回歸問題)
目標:最小化平方損失 L = 1 2 ( y i ? F ( x i ) ) 2 L = \frac{1}{2}(y_i - F(x_i))^2 L=21?(yi??F(xi?))2
偽殘差:
r i = ? ? L ? F ∣ F = F m ? 1 = y i ? F m ? 1 ( x i ) r_i = -\frac{\partial L}{\partial F} \bigg|_{F=F_{m-1}} = y_i - F_{m-1}(x_i) ri?=??F?L? ?F=Fm?1??=yi??Fm?1?(xi?)
葉子權重(設 λ = 0 \lambda=0 λ=0):
w j ? = ∑ i ∈ R j r i ∣ R j ∣ = 殘差的均值 w_j^* = \frac{\sum_{i \in R_j} r_i}{|R_j|} = \text{殘差的均值} wj??=∣Rj?∣∑i∈Rj??ri??=殘差的均值
模型更新:
F m ( x ) = F m ? 1 ( x ) + ν ∑ j = 1 J w j 1 ( x ∈ R j ) F_m(x) = F_{m-1}(x) + \nu \sum_{j=1}^J w_j \mathbf{1}(x \in R_j) Fm?(x)=Fm?1?(x)+νj=1∑J?wj?1(x∈Rj?)
💡 關鍵洞察:GBDT 將優化問題轉化為函數空間的梯度下降,每棵樹對應一次梯度更新。實際應用優先選擇改進算法(XGBoost/LightGBM/CatBoost),它們在效率、準確性和工程實現上均有顯著提升。















--傳遞參數、設備屬性)



