一、PMSM 電機參數介紹
1.1 轉子極數
轉子極數 (Rotor Poles) :三相交流電機每組線圈都會產生 N、S 磁極,每個電機每相含有的永磁體磁極個數就是極數。由于磁極是成對出現的,所以電機有 2、4、6、8……極 (偶數)。
未知參數的電機,可以通過快速的將轉子轉動一周,觀察示波器上出現線電壓峰值出現的次數即為電機的極數。也可以用另一個電機以已知的轉速拖動待測電機來得到極數。
1.2 定子電阻
定子電阻 (Stator Resistance) 是指電樞內部 (定子線圈) 的電阻,一般指相電阻 (單位為:Ω)。可以通過對未知參數的電機測試得到三種組合 (U-V,V-W,W-U) 的線電阻值,電機線電陽之和后除 2得到。
1.3 DQ 軸電感
永磁同步電機根據永磁體的安裝方式不同可分為兩類:
表貼式永磁同步電機 (SM-PMSM) 和嵌入式永磁同步電機 (IPMSM)。
1.3.1 表貼式永磁同步電機 (SM - PMSM)
表貼式電機 (SM - PMSM),也叫隱極電機,本身具有各向同性的結構,即直軸和交軸 (Ld 和 Lq) 是相同的。通常情況下,其機械結構產生更廣泛的氣隙,這反過來又意味著弱磁能力更低。
1.3.2 嵌入式永磁同步電機 (IPMSM)
內轉子式電機 (IPMSM),也叫凸極電機,顯示出各向異性結構 (LdㄑLq) 這一特殊的磁場結構可以用來產生更大的電磁轉矩。具有優良的機械結構,通常氣隙很狹窄,從而弱磁能力更好。
1.3.3 鑒別 SM-PMSM 和 IPMSM 電機
將電機從電路中斷開,用電感表接在電機的線一線端,非常地緩慢轉動電機轉子 (要防止感應電壓對測量的影響),如果電感表示數的最大值最小值差別不大 (小于 10%),說明該電機為表面磁鋼永磁電機 (SPM),此時可以將兩個值取平均即為電機相電感 (L=Lq=Ld);否則為內嵌磁鋼永磁電機(IPM),且電感表測得數值的最大值為 2 倍的 Lq,最小值為 2 倍的 Ld (對于 Y 形接法的電機來說,電感表測得的數據是兩相繞組串連的電感)。
1.3.4?SM-PMSM 和 IPMSM 電機結構差異
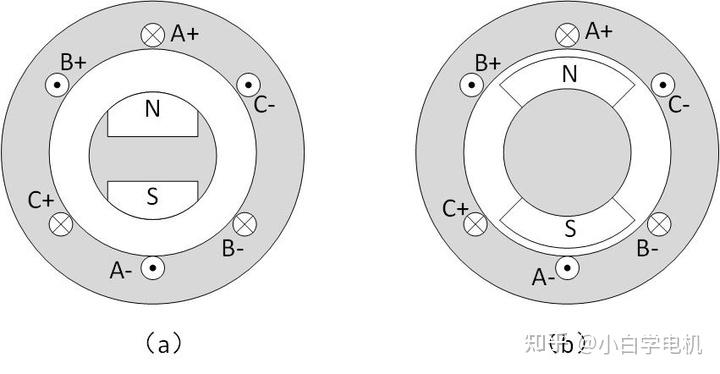
電機的 d 軸和 q 軸是一個很重要的概念,他們是相對于轉子而言的。對于電機來說,d 軸即轉子磁鋼磁極所在軸線,方向是從 S 極指向 N 極。q 軸與 d 軸垂直,方向逆時針沿 d 軸轉過 90 度。說是凸極隱極,其實是根據 d 軸和 q 軸的同步電感來確定的。
圖 (a) 是內嵌式永磁同步電機,即凸極永磁同步電機:
內嵌式永磁同步電機里頭d軸方向的用鐵量比較少,因為除了空氣氣隙,還有永磁體占用了一定空間。永磁體磁導率相當于空氣,而鐵的導磁率約為 200~400 Ur 。?q 軸除了空氣氣隙就是鐵了,用鐵量比 d 軸要多,所以 d 軸電感小,q 軸電感大。
圖 (b) 是表貼式永磁同步電機,即隱極永磁同步電機:
而隱極的磁鐵是在氣隙里頭的,d 軸方向和 q 軸方向用鐵量一樣多,所以 d 軸和 q 軸的電感相等。
?其中磁路 IPMSM 磁路如下:

1.3.5 電機的凸級效應
SM-PMSM 相當于是 dq 軸磁導率相同,而 IPMSM 的 dq 軸磁導率不同。這種磁路不對稱性稱為凸極效應,凸極率定義為? IPMSM 的
,而表貼式電機(SPMSM)因氣隙均勻?
。
1.4 轉矩常數
電動機所產生轉矩的比例系數,一般表示每安培電樞電流所能產生的轉矩大小,單位 nm/A。
1.5 反電動勢系數
電動機旋轉時,電樞繞組內部切割磁力線所感應的電動勢相對于轉速的比例系數,也稱為發電系數或感應電動勢系數。單位 V/Krpm。
1.6 轉動慣量
具有質量的物體維持其固有運動狀態的一種性質。電機轉子和負載轉動慣量之和 (單位為:kgm2),慣量會影響到速度環 PI 調節器的比例和積分增益,還有開環啟動階段的加速度。如果無法得到準確的值,可以用手轉動電機和負載根據電機轉子的轉動慣量來大致估計整體的轉動慣量。
1.7 最大電流
電機最大電流 (單位為:A) 該參數比較重要,應盡可能準確,因為涉及到電機的工作的標么電流大小。
1.8 額定轉速
電機額定轉速 (單位為:PRM) 電機能達到最大扭矩輸出的最高轉速
1.9 磁通量
磁通量 (單位為:mWb) 電機轉子永磁體磁通量大小。
二、電機的一些基礎公式和概念
2.1 反電動勢相關
2.1.1 反電動勢電壓與輸入電壓關系
反電動勢不會高于輸入電壓
?= 供給電機的電壓
?= 反電動勢的電壓
?= 電機自身的內阻所消耗的電壓
2.1.1 反電動勢公式
?= 反電動勢
?= 線圈匝數
?= 磁場的變化率 (T)
?= (θ?為磁場方向與線圈法向的夾角)
?=?
?(磁通量)
?= 線圈截面積 (
)
?= 產生磁場變化所經歷的時間 (s)
2.1.2?電機定子繞組的功率關系
?= 電源供給給電動機的功率(輸入功率)
?= 電動機輸出的機械功率
?= 熱功損(銅損、鐵損、機械損等)
2.1.3?電機定子繞組電流公式
?= 反電動勢
?= 外加電壓
?= 表示電動機回路總電阻
2.2 安培力相關
安培力公式:
?= 表示磁感應強度
?=?表導體棒的長度
?=?導體棒切割的速度
常理可知,電機反電動勢不會大于供給的電壓,加入我們給電機輸入10V 電壓,反電動勢將不會超過 10V。
對于一個電機參數來說,B 和 L 是已知的,E 也不會超過輸入電壓,我們就可以根據這個公式推算出 v,進而得到電機空轉的理論的最大值。
2.2?磁鏈相關
2.2.1 電機磁鏈常數定義 ( )
)
??定義??:?是永磁體在定子繞組中產生的固定磁鏈幅值,單位為韋伯 (Wb)。其大小由永磁體的材料特性(如剩磁 Br?)、體積和充磁方向決定,理想情況下為常數??,但實際受溫度影響 (如釹鐵硼永磁體溫度每升高100℃,下降10%~15%)
電機旋轉時,?切割定子繞組產生反電動勢:
?=?反電動勢
?= 電角速度
2.2.2 電機繞組磁鏈定義(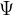 )
)
繞組磁鏈是指??定子繞組中由電流和永磁體共同作用產生的總磁通量??,單位為韋伯 (),??隨電流、轉子位置 (
) 和時間變化,是電機控制的核心變量。
- 感磁鏈??:由定子電流通過繞組自感 (
) 產生。
- ??互感磁鏈??:其他繞組電流通過互感耦合產生(如三相繞組間的相互作用)。
- 永磁體耦合磁鏈??:永磁體磁場在定子繞組中的投影分量 (
)。?
2.2.3 繞組磁鏈 (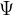 ) 和磁鏈常數? (
) 和磁鏈常數? ( ) 的區別
) 的區別
電機繞組磁鏈?:
- 定義:與電機繞組交鏈的磁通總和,由電流激勵或永磁體產生。
- 物理意義?:反映繞組與磁場的耦合程度,直接影響反電動勢和轉矩。
- 動態性?:隨電流、轉子位置變化(如Ld?id?為電流激勵分量,ψf?為永磁體固定分量)
電機磁鏈常數:
- 定義:?永磁體單獨產生的磁鏈,是固定值,單位韋伯(Wb)。
- 固定性:固定值 (除非溫度影響Br?)。
2.3 轉矩方程
對于嵌入式永磁同步電機 (IPMSM) 力矩方程是:
?= 永磁轉矩,與q軸電流成正比
?= 磁阻轉矩,由 d-q 軸電感差異和電流交互作用產生。
表貼式 (SPMSM) 則是:
因為??其磁阻轉矩為 0,所以控制表貼式電機獲得最大轉矩控制 id=0 即可。
三、定子三項電壓方程:
3.1 定子三項電壓方程 (磁鏈表達)
?= 相電壓
?= 相電流
?= 相磁鏈
?= 相電阻
三項矩陣形式如下,其中 P 為微分算子:
?
其中,、
、
?是三相定子電壓,
?是定子電阻,是是子電流,
、
、
?是定子磁鏈,
、
、
。為電角度和實際電機角度不同,此方程組電機控制過程中應用情況較少。注意:定子磁鏈是一個多變量、強耦合的結果,所以用電橋測試電感時,慢速旋轉電機,電感的值一直在變化。
3.2 磁鏈方程
電機的磁鏈電流產生和永磁體與繞組有關:

、
、
?= 轉子永磁體磁鏈常數
、
、
?= 各自繞組的自感
、
、
?= 相間互感,對稱系統中?
、
、
?= 三項定子電流
?= 永磁體磁鏈幅值 (常數)
?= 轉子 d?軸與 A 相繞組的電角度
對于 B、C 相的反電動勢和角度的關系正好是相差 120°,所以上述公式需要減去和加上?。

3.3?磁鏈方程的微分形式
簡化之前的磁鏈方程,此方程只描述靜態系統所以忽略角度:
?= 定子繞組的電感,包括自感和互感
?= 永磁體磁鏈幅值 (常數)
如果看做成一個動態系統需要加入電角度:
我們將其取微分可得:
其中??(轉子電角速度),因為最終取微分可得:
?= 永磁體磁鏈幅值 (常數)
?= 定子繞組的電感,包括自感和互感
?= 電角速度
3.3?定子三項電壓方程 (電感微分與磁鏈峰值常數表達)
還是回到這個方程:
其中磁鏈等于:
也就是對??取微分可得:
![]()


所以最終我們得出:

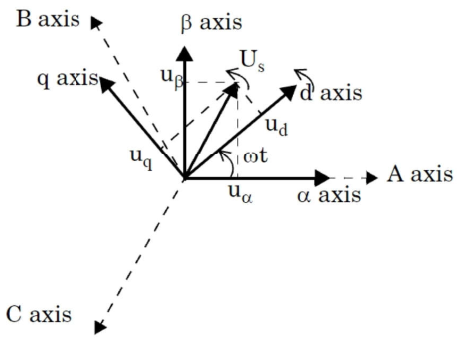
其中? ?矢量圖如下:
?矢量圖如下:

四、兩項電機方程
4.1 α 和 β 軸的靜止電壓方程
對 ABC 三相電壓方程做 Clake 變換得到 uα、uβ?靜止電壓方程。

eα、eβ 是兩軸反電動勢的公式。

這兩個方程一般用作無傳感器角度觀測,需牢記,表貼式電機 、
?相等,內嵌式電機?
、
?不相等。
?4.2 d 和 q 軸旋轉坐標電壓方程
再做 Park 變換得到兩項電壓 d、q 軸下的電壓方程。


4.3 d 和 q 軸的磁鏈方程
對于 IPMSM 電機來說 dq 軸電感不相同,公式如下:

SPMSM 電機 dq 電感軸相等,簡化為:
![]()
4.2 d 和 q 軸的電磁轉矩方程
?= d 軸電感
?= q 軸電感
?= 磁鏈常數
?= 極對數
?= 電機轉矩
其中,、
、
?為電機本體參數,需測定。
?為電機極對數。此方程已完成對耦合量解耦,最后一項和轉速有關的磁鏈耦合量,可前饋消除,如果影響比較小,可以不用管。軸方程需牢記,電機實際控制需要用到,電流環,MTPA,弱磁等都需用到此方程。
五、坐標變換
5.1 Clark 變換和逆 Clark 變換
5.1.1 Clark?變換
左圖是 A、B、C 三項電流;右圖是 α、β 兩項電流
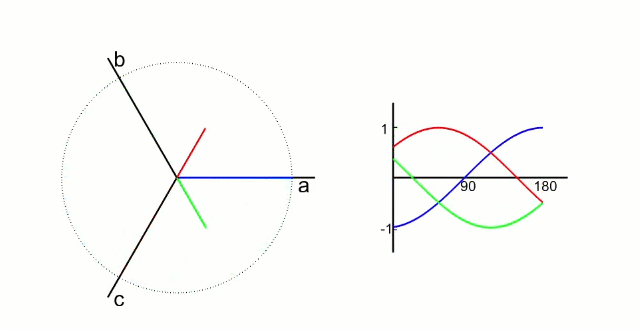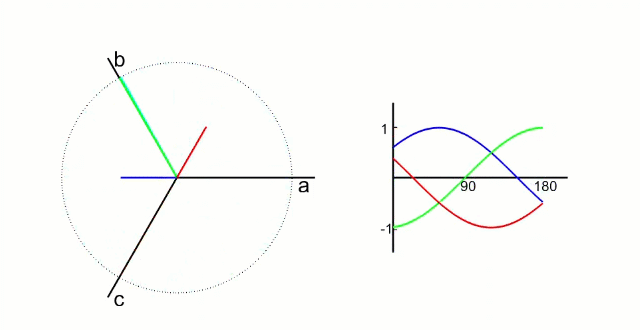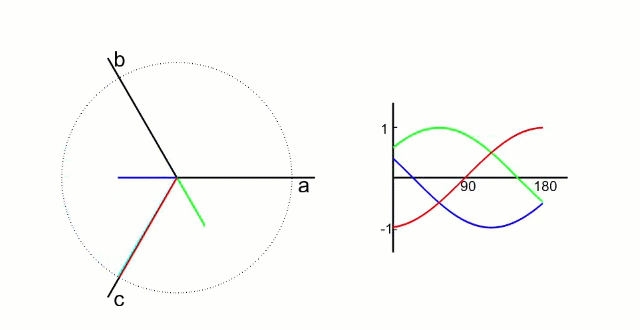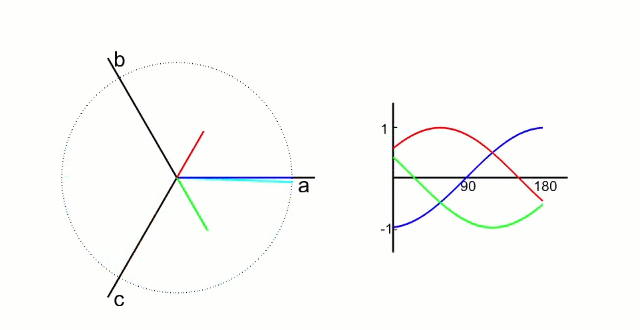
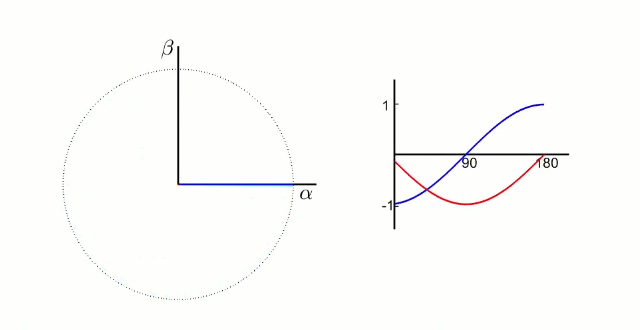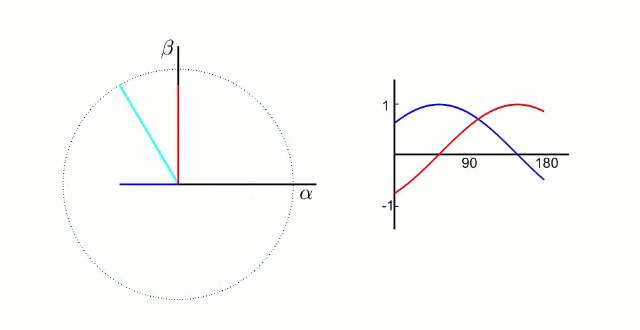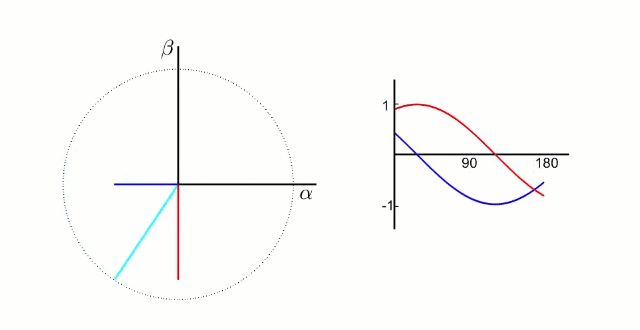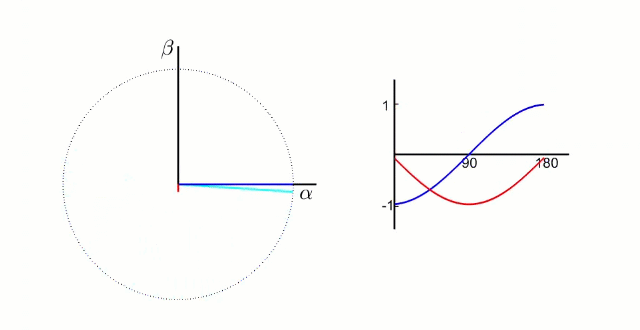
以電流變換為例,A、B、C 向 α、β 軸變換,按照幅值不變原則:
5.1.2 逆 Clark 變換?
以電流變換為例,α、β 向 A、B、C 軸變換,按照幅值不變原則:
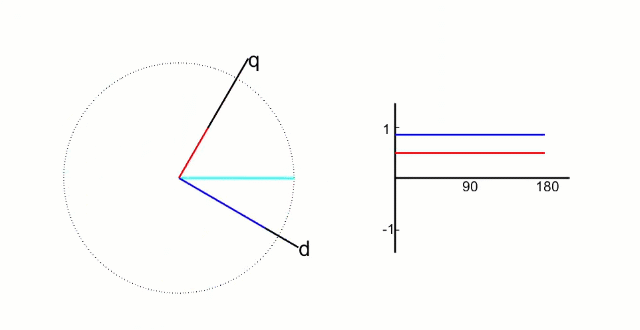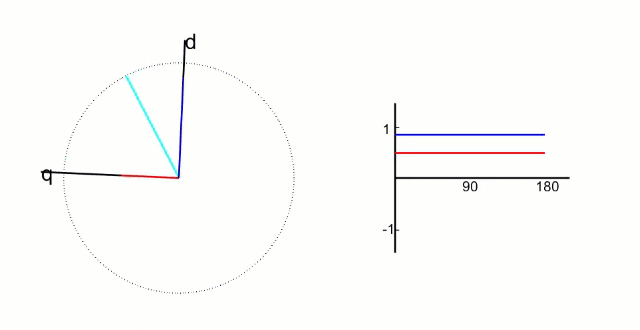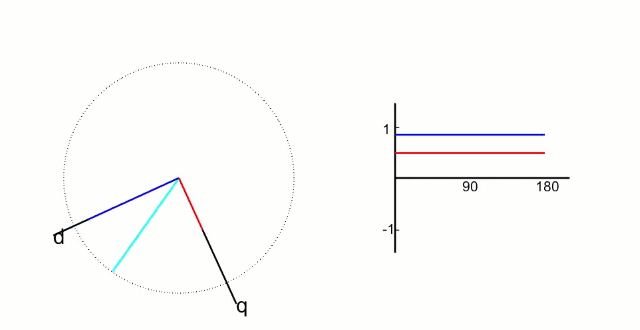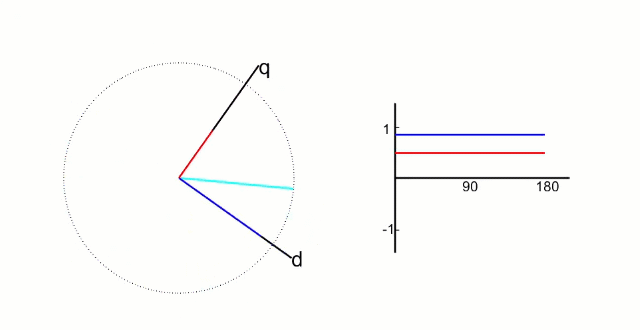
5.2 Park 變換和逆 Park 變換
左圖是?α、β 兩項電流;右圖是 DQ 軸電流
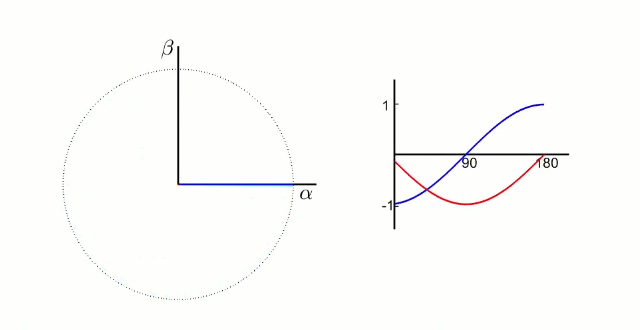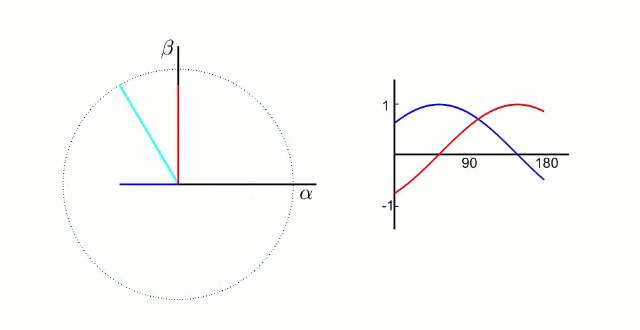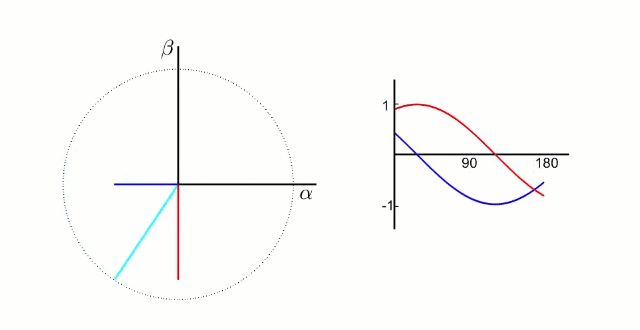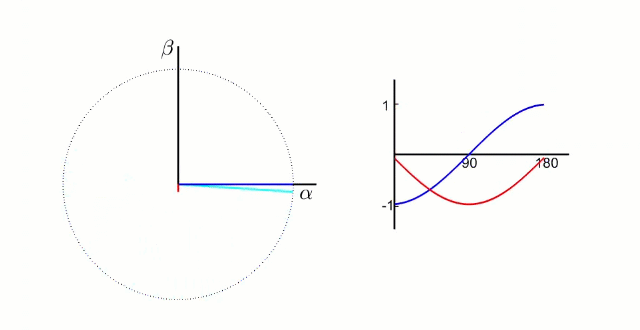









)





 和 部署方式(--deploy-mode))



