循環神經網絡 - 參數學習之隨時間反向傳播算法

本文中，我們以同步的序列到序列模式為例來介紹循環神經網絡的參數學習。

循環神經網絡中存在一個遞歸調用的函數 𝑓(?)，因此其計算參數梯度的方式和前饋神經網絡不太相同。在循環神經網絡中主要有兩種計算梯度的方式：隨時間反向傳播(BPTT)算法和實時循環學習(RTRL)算法。

本文我們來學習隨時間反向傳播算法。

BPTT 算法將循環神經網絡看作一個展開的多層前饋網絡，其中“每一層”對應循環網絡中的“每個時刻”。這樣，循環神經網絡就可以按照前饋網絡中的反向傳播算法計算參數梯度。在“展開”的前饋網絡中，所有層的參數是共享的，因此參數的真實梯度是所有“展開層”的參數梯度之和。

一、數學推導：

以隨機梯度下降為例，給定一個訓練樣本 (𝒙, 𝒚)，其中 𝒙1∶𝑇 =? (𝒙1, ? , 𝒙𝑇 )為長度是𝑇的輸入序列，𝑦1∶𝑇 =(𝑦1,?,𝑦𝑇)是長度為𝑇的標簽序列。即在每個時刻 𝑡，都有一個監督信息 𝑦𝑡 ，我們定義時刻 𝑡 的損失函數為：

其中 𝑔(𝒉𝑡) 為第 𝑡 時刻的輸出，L 為可微分的損失函數，比如交叉熵。那么整個序列的損失函數為：

整個序列的損失函數 L 關于參數 𝑼 的梯度為

即每個時刻損失 L𝑡 對參數 𝑼 的偏導數之和。

基于參數 𝑼 和隱藏層在每個時刻 𝑘(1 ≤ 𝑘 ≤ 𝑡) 的凈輸入有關，通過數學推導（推導過程比較復雜，這里略過，大家著重掌握公式），可以得出：

計算偏導數：

得到整個序列的損失函數 L 關于參數 𝑼 的梯度：

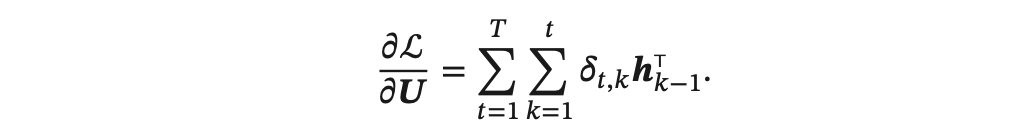
同理可得，L 關于權重 𝑾 和偏置 𝒃 的梯度為：

其中，類似前饋神經網絡中的誤差項為：

定義以下誤差項為第 𝑡 時刻的損失對第 𝑘 時刻隱藏神經層的凈輸入 𝒛𝑘 的導數，則當 1 ≤ 𝑘 < 𝑡 時

由上可以看出誤差項，時刻k的𝛿𝑡,𝑘可以由時刻k+1的𝛿𝑡,𝑘+1得出，即所謂的反向傳播。

下圖給出了誤差項隨時間進行反向傳播算法的示例：

二、進一步理解隨時間反向傳播算法BPTT

BPTT 的具體實現核心在于將 RNN 在時間維度上“展開”，從而把整個循環網絡視作一個深層的前饋網絡，然后利用反向傳播算法計算每個時間步的梯度。以下是關鍵步驟：

（一）前向傳播（Forward Pass）

在前向傳播階段，模型從初始隱藏狀態開始，按時間順序依次處理輸入序列的每個時間步。在每個時間步 t?中，RNN 會計算出當前隱藏狀態 ht：

同時，根據隱藏狀態產生輸出：

這些中間狀態和輸出都被存儲下來，供之后的反向傳播使用。

（二）損失計算

對于整個序列的輸出，我們會計算一個總體損失 LL，它通常是所有時間步損失 LtL_t 的求和或平均：

例如，在一個回歸或分類任務中，可能使用均方誤差或交叉熵作為每個時間步的損失。

（三）時間展開（Unrolling）

為了使反向傳播適用于循環結構，我們把 RNN 展開成一個由 T?個層組成的前饋網絡，每一層對應一個時間步。雖然這些層共享同一組參數，但在展開的過程中，各個時間步之間的依賴關系（主要是隱藏狀態 ht）得以顯現。

這樣做的目的是為了使我們能夠用標準的反向傳播算法計算梯度，從而更新整個序列中共享的參數。下面通過一個簡單的例子說明這一過程。

假設情景

假設我們有一個 RNN 模型，用來處理一個長度為 3 的輸入序列 [x1,x2,x3]（例如數值 1、2、3），初始隱藏狀態 h0? 設為零。模型的前向計算公式為：

將 RNN 展開成前饋網絡

原始的 RNN 是通過循環實現的，即使用同一組參數不斷將隱藏狀態從前一步傳遞到下一步。為了直觀地理解反向傳播的過程，我們將其在時間軸上展開，即把每個時間步看作網絡中的一層，這些層之間按照時間順序相連。

對于我們的序列，有如下展開：

時間步 1
時間步 2
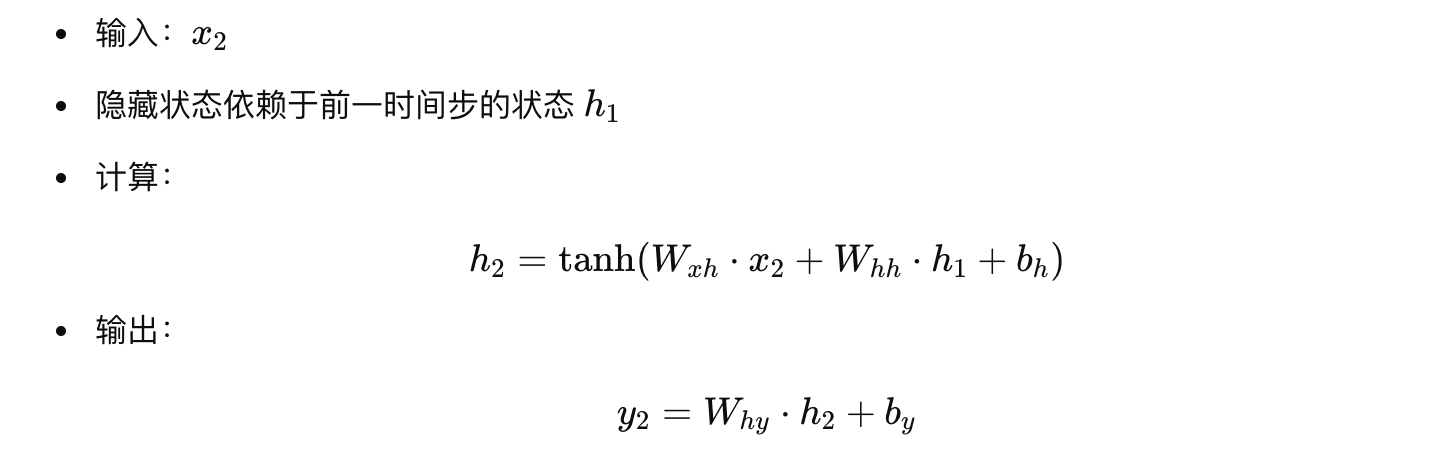
時間步 3

這整個過程就像一個前饋網絡，共有 3 層（不包括初始狀態），每層的輸出 h_t? 都依賴于前一層的輸出 h_{t-1}? 和當前輸入 x_t?。注意，雖然在展開過程中每一層對應一個不同的時間步，但所有層共享同一組權重和偏置。

為什么這樣展開？

這種展開方式將時序依賴“展開”到層級結構中，使得整個序列可以看成一個深層網絡。這樣有兩個好處：

便于反向傳播計算
我們可以像對普通前饋神經網絡那樣，基于鏈式法則逐層計算梯度，并且由于參數共享，每層計算的梯度會累積在同一組權重上。
捕捉長距離依賴
通過展開，我們能直觀地理解誤差如何從最后一層傳回到第一層，反映長距離依賴問題，以及梯度消失或爆炸的問題。

總結

展開過程：將 RNN 從時間步 1 到 T 展開，每個時間步視為一層前饋網絡，所有層使用同一組參數。
前向傳播：依次計算每層隱藏狀態和輸出。
反向傳播：從最后一層開始反向傳播，逐層累積梯度，更新共享參數。

這種展開不僅使得梯度計算過程清晰，而且方便我們理解如何利用 BPTT 解決時間依賴問題，確保模型能夠捕捉序列中長期和短期的信息。

（四）反向傳播（Backward Pass Through Time，BPTT）

從展開后的最后一個時間步 T?開始，依次向前計算梯度：

局部梯度計算：在每個時間步，根據當前輸出與目標之間的誤差，首先計算當前時間步的輸出層梯度，然后通過當前隱藏狀態對損失的貢獻，計算激活函數（如 tanh?）的導數。
梯度傳遞與累積：由于隱藏狀態 hth_t 不僅直接影響當前輸出，還間接影響后續所有時間步的輸出，因而需要將來自未來時間步傳回的梯度（往往稱為 “dh_next”）與當前時間步的梯度相加，形成一個總的梯度。
參數梯度更新：利用鏈式法則，通過隱藏狀態梯度計算出對輸入到隱藏權重 Wxh 和隱藏到隱藏權重 Whh 以及偏置的梯度。由于這些參數在每個時間步都是共享的，每一步計算出的梯度都會被累加起來。
時間傳遞：在完成當前時間步梯度計算后，再將梯度通過傳遞回前一個時間步，繼續重復這一過程直到第一個時間步。

下面以一個簡單的 RNN 模型展開一個長度為 3 的序列的反向傳播過程，來詳細說明 BPTT 中的四個關鍵步驟：局部梯度計算、梯度傳遞與累積、參數梯度更新、和時間傳遞。假設模型的前向傳播計算如下（激活函數采用 tanh）：

隱藏狀態更新：
輸出計算：

假設我們的損失函數 L?是所有時間步損失的加和：

其中每個時間步的損失 Lt 是模型輸出 yt 和目標 (y_t)^{target} 之間的誤差（例如均方誤差）。

下面分步詳細說明 BPTT 的反向傳播過程。

1. 局部梯度計算

在反向傳播時，我們需要先計算每個時間步在輸出端的局部梯度，然后再傳回隱藏層。具體來說：

對于時間步 t，我們先計算輸出層的梯度：
接著，通過輸出層將梯度傳遞給隱藏狀態：
由于隱藏狀態經過 tanh? 激活，，其局部梯度部分需乘上激活函數的導數：

因此，得到當前時間步的局部梯度：

其中“⊙”表示元素級相乘。

這部分稱為“局部梯度計算”，即對當前時刻輸出誤差先求到隱藏層（通過 Why?），再結合激活函數求出對 zt 的梯度。

2. 梯度傳遞與累積

由于 RNN 中隱藏狀態間存在依賴，當前時刻 ht 不僅受當前時間步損失 Lt 影響，還間接受到后續時間步的反饋。因此，反向傳播時需要將未來時間步傳回來的梯度累積在當前時刻。設我們計算總的梯度 dht? 對隱藏狀態的偏導，其計算方式為：

即當前時刻的總梯度等于當前局部梯度加上由下一時間步傳回來的梯度經過隱藏層的權重傳遞后的結果。

3. 參數梯度更新

有了每個時間步的梯度 δt? 和從后續傳來的梯度累積，我們可以對各層參數求導。具體來說：

對于 輸入到隱藏層權重 Wxh?：

其中 ? 表示外積，此處對每個時間步將 δt 與相應的輸入 xt 外積，然后累加。
對于 隱藏到隱藏層權重 Whh?：

同樣每個時間步累加當前梯度與前一隱藏狀態的外積。
對于 隱藏層偏置 bh?：
對于 隱藏到輸出層權重 Why?，輸出層的梯度已經在局部步驟中計算：
.
對于 輸出偏置 by?：

這些梯度在反向傳播過程中在每個時間步內計算完畢后，通過累加得到整個序列上的梯度，接著就可以用常規優化方法更新參數。

4. 時間傳遞（從未來到過去）

在反向傳播過程中，必須將未來時間步的梯度傳遞到當前時間步，這就是“時間傳遞”。具體步驟為：

這種梯度傳遞過程在整個序列反向迭代中重復執行，從時間步 T?逐層傳回到時間步 1。

綜合一個詳細例子

假設我們有一個時間序列長度為 3 的 RNN，且以時間步 t=3 開始反向傳播。簡化起見，以下給出各步描述：

時間步 3：
時間步 2：
時間步 1：

總結

局部梯度計算：在每個時間步，根據輸出誤差乘以輸出層權重和激活函數導數，得到對當前隱藏單元輸入的梯度（δt?）。
梯度傳遞與累積：從后向前逐步將未來時刻的梯度通過隱藏層（乘以和激活導數）傳遞給前一時間步，累加成當前時刻的總梯度。
參數梯度更新：利用每個時間步局部梯度與輸入（或前一時刻隱藏狀態）的外積，累積得到 Wxh?、Whh? 和 bh? 的梯度；輸出層參數的梯度也由對應輸出誤差累積。
時間傳遞：通過計算隱藏狀態之間的依賴（即 ??），將梯度從后續傳遞給當前，直至序列首端。