---

兩數之和

題目解析

---

思路

解法一 ：暴力枚舉 依次遍歷

• 時間復雜度 O(n^2)
  暴力枚舉兩層for()循環遍歷O(n^2)
• 空間復雜度 無

1. 先固定其中一個數
2. 依次與該數之前的數相加

而 解法二 則是，遍歷完這個數以后，將其丟入hash表中。枚舉下一個數時，很自然的枚舉hash表中前面遍歷過的數

解法二 ：使用哈希表來做優化

• 時間復雜度：O(n)
  由原來的 暴力枚舉兩層for()循環遍歷O(n^2) 到 ，只需遍歷一遍 固定一個數O(n)，哈希表查找匹配的另一個數O(1)

• 空間復雜度：O(n)
  對比 暴力枚舉 即可看出，哈希表是用 空間換時間

---

核心邏輯

為什么之前的暴力枚舉策略不太好用了？

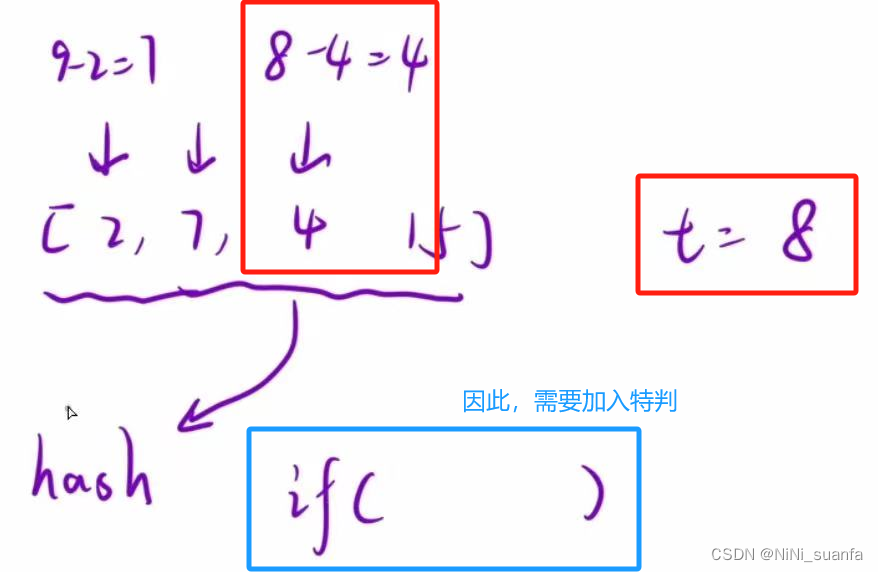
我們也能把所有的數都放入hash表中，再由前往后遍歷一遍數組，再直接在hash中找匹配的數就好了，為什么還要 逐一遍歷，再將遍歷到的節點逐一放入hash表中 ？

這是因為會出現 “恰好 遍歷到的數本身，也能滿足匹配的要求” 的情況，這違反了題目所說的需求 數組中同一個元素在答案里不能重復出現

blog.csdnimg.cn/direct/4e384c8f2ebd454f910606e12c610d2c.jpeg)

因此，這種做法需要加入特判。

所以，這就是 這道題選擇 固定一個數，再與其前面的數逐一對比完后，再將其自身放入hash表中，參與匹配 的原因

因此，循環遍歷固定一個節點，遍歷完后將該節點放入hash表中，后繼續向后遍歷，僅需查找前面放入hash表中的值即可（就不會出現查找hash表中選中自身的情況），這樣的順序避免了 出現了重復出現同一個數字 的情況 。也 不需要再處理什么邊界情況 了。

---

代碼實現

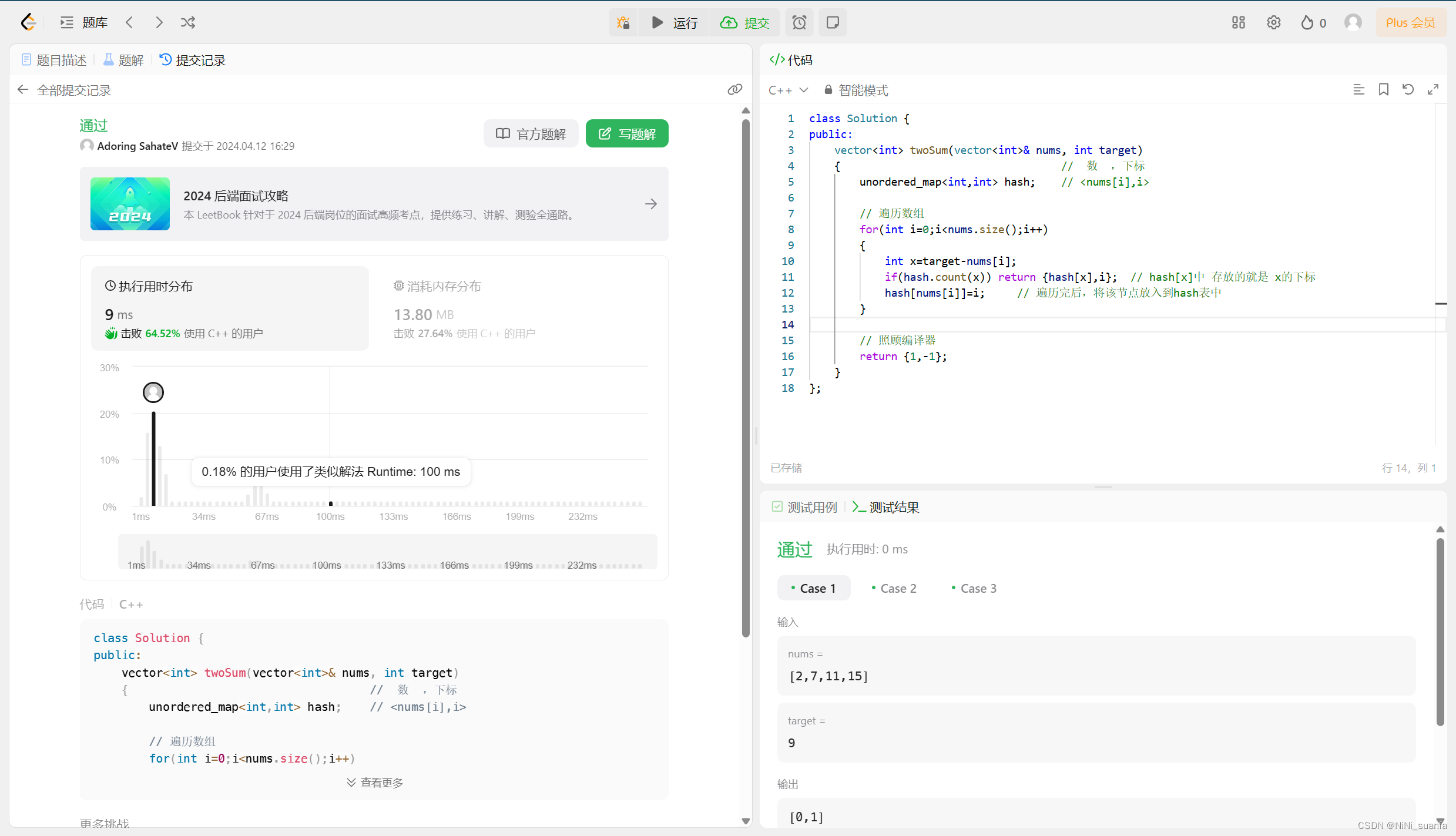
class Solution {
public:vector<int> twoSum(vector<int>& nums, int target) {                                   //  數  ，下標unordered_map<int,int> hash;    // <nums[i],i>   // 遍歷數組for(int i=0;i<nums.size();i++){int x=target-nums[i];if(hash.count(x)) return {hash[x],i};  // hash[x]中 存放的就是 x的下標hash[nums[i]]=i;     // 遍歷完后，將該節點放入到hash表中}// 照顧編譯器return {1,-1};}
};