堆：

• 此處堆為二叉樹的應用，不是計算機中用于管理動態內存的堆。
• 形狀是完全二叉樹。
• 堆分兩種：最大堆，最小堆。
• 最大堆：每個節點比子樹所有節點的數值都大，根節點為最大值。
• 最小堆：每個節點比子樹所有節點的數值都小，根節點為最小值。
• 左右節點的數值沒有順序要求，但有左子節點才能有右子節點。
• 一般用數組實現堆。最小堆可以實現優先隊列。

注：完全二叉樹：每個節點最多2個節點，倒數第二層級（含）之前層級的所有節點都有元素，最后一層級從左到右依次有元素（中間不能斷）。

子樹：節點及其所有子節點形成子樹。（即節點，左右子節點，左右子節點的左右子節點，。。。）

根節點：沒有父節點。

兄弟節點：其父節點是同一個節點。

父子節點在數組中的索引號

節點	索引號（根節點為0）
節點	x
父節點	（x-1）// 2
左兄弟節點（右節點才有）	x - 1
右兄弟節點（左節點才有）	x + 1
左子節點	2x + 1
右子節點	2x + 2

---

C語言實現：（使用數組實現最小堆）

創建堆（結構體數據類型）：記錄數組地址和元素個數

// 堆（結構體數據類型）
typedef struct Heap
{int *p;			// 記錄數組地址int n;			// 記錄元素個數
} Heap;             // 別名

?（函數）堆初始化：

// 堆初始化
void init(Heap *heap, int length)
{heap->p = (int *)malloc(length * sizeof(int));    // 分配內存空間if(heap->p == NULL){perror("Memory allocation failed");exit(-1);}heap->n = 0;            // 元素個數，初始化為0
}

?創建堆變量，并初始化

Heap heap;         // 創建堆變量
init(&heap, 8);    // 設置數組最大元素個數為8

添加元素：

1、先在末尾添加元素。

2、（向上調整）與父節點比較大小，若小于父節點，與父節點交換位置，直到開頭位置（根節點，數組第一個元素）。

（注：子節點索引號為x，父節點索引號為(x-1)//2）

void add(Heap *heap, int data)		// add a element to the heap
{// 往末尾添加元素heap->p[heap->n] = data;// (向上調整) 與父節點比較，小于父節點的值，與父節點交換位置int cur = heap->n;while(cur > 0){int parent = ceil((cur - 1) / 2);if(heap->p[parent] > data){heap->p[cur] = heap->p[parent];heap->p[parent] = data;cur = parent;}else break;}// 每添加一個元素，元素個數+1heap->n++;
}

刪除（根節點）：

1、記錄根節點（數組第一個元素）和末尾節點（數組最后一個元素）。

2、末尾節點的值換到根節點位置，元素個數-1。

3、（向下調整）從根節點開始，依次與左右子節點比較大小，數值小的是父節點，直到比對到末尾。

（注：父節點索引號為x，左子節點索引號為2x+1，右子節點索引號為2x+2）

int delete(Heap *heap)			// delete root from the heap
{if(heap->n == 0) return -1;    // 空樹heap->n--;                     // 每刪除一次根節點，元素個數-1int root = heap->p[0], enddata = heap->p[heap->n];heap->p[0] = enddata;	       // 末尾元素換到第一個位置// (向下調整) 與左右子節點比較，若子節點小，與較小子節點交換位置int cur = 0;while(cur <= heap->n){int left = cur * 2 + 1, right = cur * 2 + 2, minchild;if(left > heap->n) break;				// 沒有左子節點if(right > heap->n) minchild = left;	// 沒有右子節點，有左子節點else									// 左右子節點都有的情況{// 左右子節點比較，找到較小子節點if(heap->p[right] < heap->p[left]) minchild = right;else minchild = left;// 父節點與較小子節點比較，若子節點小，與子節點交換位置if(heap->p[minchild] < enddata){heap->p[cur] = heap->p[minchild];heap->p[minchild] = enddata;cur = minchild;}else break;}}return root;
}

獲取根節點：（數組第一個元素）

int getroot(Heap *heap)			// get the root from the heap
{if(heap->n == 0){printf("Empty heap\n");exit(-1);}return heap->p[0];
}

遍歷堆：（類似廣度遍歷二叉樹）

每個節點比子樹的所有節點都小，但左右節點沒有順序要求。

void traverse(Heap *heap)		// show element one by one (like breadth traverse the tree)
{if(heap->n == 0) return ;printf("elements(%d): ", heap->n);for(int k = 0; k < heap->n; k++){printf("%d  ", heap->p[k]);}printf("\n");
}

清空堆：

釋放數組內存空間，指向數組的指針指向NULL，元素個數為0。

void clear(Heap *heap)		// clear the heap (free memory space of the array)
{free(heap->p);          // 釋放數組內存空間heap->p = NULL;         // 指針指向NULL，避免野指針heap->n = 0;            // 元素個數為0
}

?

---

完整代碼：（heap.c）

#include <stdio.h>
#include <math.h>
#include <stdlib.h>/* structure */
typedef struct Heap
{int *p;			// memory address of the heap (array)int n;			// the number of the heap
} Heap;/* function prototype */
void init(Heap *, int);		// heap initialization
void add(Heap *, int);		// add a element to the heap
int delete(Heap *);			// delete root from the heap
int getroot(Heap *);		// get the root from the heap
void traverse(Heap *);		// show element one by one (likely breadth traverse the tree)
void clear(Heap *);			// clear the heap (free memory space of the array)/* main function */
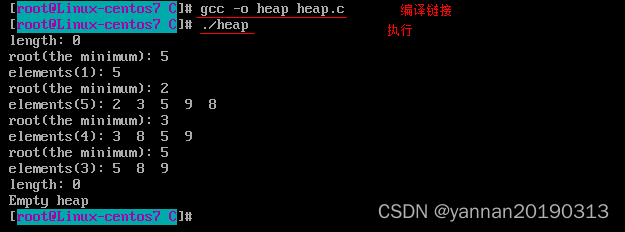
int main(void)
{Heap heap;init(&heap, 8);printf("length: %d\n", heap.n);add(&heap, 5);	printf("root(the minimum): %d\n", getroot(&heap));traverse(&heap);add(&heap, 8);	add(&heap, 3);	add(&heap, 9);	add(&heap, 2);printf("root(the minimum): %d\n", getroot(&heap));traverse(&heap);delete(&heap);	printf("root(the minimum): %d\n", getroot(&heap));traverse(&heap);delete(&heap);	printf("root(the minimum): %d\n", getroot(&heap));traverse(&heap);clear(&heap);printf("length: %d\n", heap.n);printf("root(the minimum): %d\n", getroot(&heap));return 0;
}/* subfunction */
void init(Heap *heap, int length)		// heap initialization
{heap->p = (int *)malloc(length * sizeof(int));if(heap->p == NULL){perror("Memory allocation failed");exit(-1);}heap->n = 0;
}void add(Heap *heap, int data)		// add a element to the heap
{// add a element to the end of the heapheap->p[heap->n] = data;// (adjust up) compair with parent,if smaller than parent, change the positionint cur = heap->n;while(cur > 0){int parent = ceil((cur - 1) / 2);if(heap->p[parent] > data){heap->p[cur] = heap->p[parent];heap->p[parent] = data;cur = parent;}else break;}heap->n++;
}int delete(Heap *heap)			// delete root from the heap
{if(heap->n == 0) return -1;heap->n--;int root = heap->p[0], enddata = heap->p[heap->n];heap->p[0] = enddata;	// put the last element to the first position// (adjust down) compair with left and right child, minimun is parentint cur = 0;while(cur <= heap->n){int left = cur * 2 + 1, right = cur * 2 + 2, minchild;if(left > heap->n) break;				// no left childif(right > heap->n) minchild = left;	// have left child, no right childelse									// have left child and right child{// compair left child and right child, find smaller oneif(heap->p[right] < heap->p[left]) minchild = right;else minchild = left;// smaller child compair with parent,if child is the smallest, changeif(heap->p[minchild] < enddata){heap->p[cur] = heap->p[minchild];heap->p[minchild] = enddata;cur = minchild;}else break;}}return root;
}int getroot(Heap *heap)			// get the root from the heap
{if(heap->n == 0){printf("Empty heap\n");exit(-1);}return heap->p[0];
}void traverse(Heap *heap)		// show element one by one (like breadth traverse the tree)
{if(heap->n == 0) return ;printf("elements(%d): ", heap->n);for(int k = 0; k < heap->n; k++){printf("%d  ", heap->p[k]);}printf("\n");
}void clear(Heap *heap)		// clear the heap (free memory space of the array)
{free(heap->p);heap->p = NULL;heap->n = 0;
}

編譯鏈接： gcc -o heap heap.c

執行可執行文件：?./heap

?