浮點型變量
前言
上一篇文章我們研究了整數類型變量,本次我們來開始研究一下浮點類型變量。

浮點類型
浮點數在計算機編程中扮演著重要的角色。它們是一種特殊的數據類型,用于存儲和處理小數或實數。在Python中,浮點數是由小數點分隔的數字組成的。在本文中,我將探討浮點類型變量的定義、使用以及它們的一些特點。
首先,讓我們來看看浮點數變量的定義。在Python中,可以使用以下語法來定義一個浮點變量:
variable_name = 3.14
print(variable_name)
最后得到的結果如下圖所示:
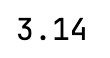
在上面的例子中,variable_name是變量的名稱,而3.14是變量的值。注意,浮點數可以是正數或負數,并且可以包含小數點。
接下來,讓我們探討一些使用浮點類型變量的例子。假設我們要計算一個圓的面積。我們知道圓的面積公式是πr^2,其中π是一個數學常數,約等于3.14,而r是圓的半徑。我們可以使用浮點類型變量來存儲半徑和計算面積的結果。下面是一個計算圓面積的示例代碼:
pi = 3.14
radius = 5.0area = pi * (radius ** 2)
print(area)
運行結果如下所示:

在上面的例子中,我們定義了一個名為pi的浮點變量,該變量存儲了常數π的近似值3.14。然后,我們定義了一個名為radius的浮點變量,該變量存儲了圓的半徑。接下來,我們使用浮點數的乘法和冪運算,計算圓的面積,并將其存儲在名為area的浮點變量中。最后,我們使用print函數將計算結果打印出來。
除了基本的數學計算,浮點類型變量在實際編程中還有許多其他的應用。例如,它們可以用于存儲和處理貨幣值、測量數據、科學計算等。浮點數的范圍通常比整數的范圍大,因此它們可以表示更大或更小的值。然而,浮點數的精度是有限的,這意味著它們可能無法準確地表示某些十進制數。這是因為計算機內部使用二進制表示浮點數,并且存在舍入誤差。因此,在進行關鍵的精確計算時,我們需要小心處理浮點數。
此外,浮點數還可以表示為特殊值NaN(Not a Number),表示一個無效的或未定義的數值。NaN通常出現在一些非法的數學運算中,比如0除以0。NaN的特點是無法進行比較,任何與NaN進行的比較操作都將返回False。
在Python中,處理浮點數的功能非常強大。Python提供了許多內置函數和模塊,用于處理浮點數。這些功能包括數學運算、舍入和格式化等。例如,Python提供了math模塊,其中包含了許多數學函數,如sin、cos、sqrt等。另外,Python還提供了round函數來進行舍入操作,可以將浮點數四舍五入到指定的小數位數。此外,Python還提供了format函數來格式化浮點數輸出,可以指定輸出的精度、寬度和對齊方式等。
總之,浮點數是一種用于表示小數的數據類型,在計算機中以近似的方式存儲和處理實數。除了常規的浮點數,還有特殊值如正無窮大、負無窮大和NaN。Python提供了豐富的功能和工具來處理浮點數,包括數學運算、舍入和格式化等。
下面我們來看一下詳細的代碼
import math# 浮點數運算
a = 1.2
b = 2.3
c = a + b
print(c) # 輸出:3.5# 舍入操作
d = 3.14159
e = round(d, 2)
print(e) # 輸出:3.14# 格式化輸出
f = 4.56789
formatted_f = "{:.2f}".format(f)
print(formatted_f) # 輸出:4.57# 使用math模塊進行數學運算
g = math.sin(math.pi)
print(g) # 輸出:1.2246467991473532e-16# 特殊浮點數值
h = float('inf')
i = float('-inf')
j = float('nan')
print(h, i, j) # 輸出:inf -inf nan

這段代碼主要介紹了Python中浮點數的運算和操作。
- 首先,代碼導入了math模塊,該模塊提供了一系列數學運算的函數和常量。
- 然后,定義了兩個浮點數a和b,進行加法運算,并將結果賦值給變量c。使用print函數打印出c的值,結果為3.5。
- 接下來,定義了一個浮點數d,并使用round函數將其四舍五入保留兩位小數,將結果賦值給變量e。使用print函數打印出e的值,結果為3.14。
- 然后,定義了一個浮點數f,并使用format函數將其格式化為保留兩位小數的字符串形式,將結果賦值給變量formatted_f。使用print函數打印出formatted_f的值,結果為4.57。
- 接下來,使用math模塊的sin函數計算了π的正弦值,并將結果賦值給變量g。使用print函數打印出g的值,結果為1.2246467991473532e-16,這是一個科學計數法的表示方式。
- 最后,定義了三個特殊的浮點數值:正無窮大、負無窮大和非數值。使用print函數打印出h、i、j的值,分別為inf、-inf、nan。
深入了解浮點數底層
在Python中,float 類型用于表示浮點數,即帶有小數部分的數字。雖然Python為程序員提供了高級別的抽象,使得我們不需要關心底層實現的細節,但了解float類型在Python內部如何表示和存儲仍然是有益的。
IEEE 754 浮點數標準
Python中的float類型通常遵循IEEE 754標準來表示浮點數。IEEE 754是一個定義浮點數在計算機中如何表示、存儲和運算的國際標準。它定義了多種精度的浮點數,包括單精度(32位)和雙精度(64位)。Python的float類型通常是雙精度(double precision)。
浮點數的構成
一個IEEE 754浮點數由三個部分組成:
- 符號位(Sign):1位,用于表示正負號(0表示正數,1表示負數)。
- 指數位(Exponent):對于雙精度浮點數,指數位占用11位。它表示了數值的指數部分,并且有一個偏移量(對于雙精度是1023)。
- 尾數位(Mantissa 或 Fraction):對于雙精度浮點數,尾數位占用52位。它表示了數值的小數部分(或稱為分數部分)。
浮點數的范圍與精度
由于指數位和尾數位的位數是固定的,因此浮點數的范圍和精度也是有限的。
- 范圍:由于指數位的限制,浮點數有一個最小值(接近但大于0)和一個最大值(有限的)。
- 精度:由于尾數位的限制,浮點數不能表示所有實數,只能表示一定精度范圍內的數。這意味著對于某些操作(如除法),結果可能不是精確的。
Python中的float類型
在Python中,當你創建一個浮點數時(例如x = 3.14),Python會將其存儲為一個遵循IEEE 754標準的雙精度浮點數。你可以使用sys.float_info來獲取有關Python中float類型的信息,包括其精度、范圍等。
浮點數的限制
由于浮點數的表示方式和精度限制,它們在某些情況下可能會導致問題:
- 舍入誤差:由于浮點數的精度有限,某些計算可能會導致舍入誤差。
- 表示范圍:非常大的數或非常小的數可能無法用浮點數精確表示。
- 特殊值:浮點數還包括一些特殊值,如正無窮大(float(‘inf’))、負無窮大(-float(‘inf’))和非數字(float(‘nan’))。
浮點數與十進制數的差異
需要注意的是,雖然我們在日常生活中經常使用十進制數,但計算機內部使用二進制數來表示和處理數據。由于二進制數無法精確表示所有十進制小數(如1/3或1/10),因此浮點數的表示和計算可能會受到這種差異的影響。這也是為什么在進行金融計算或需要高精度計算時,通常會使用專門的庫(如decimal庫)來避免浮點數的舍入誤差。
總結
總結起來,浮點類型變量在Python中起到了至關重要的作用。它們用于存儲和處理小數和實數,可以進行各種數學運算,并具有一些特殊的特點。在實際編程中,我們需要注意浮點數的精度和舍入誤差,并使用適當的函數和方法來處理浮點數。通過熟練掌握浮點類型變量的使用,我們可以更好地進行數值計算和科學編程。





)













