思路：經典的動態規劃問題：

1. dp[i][j]表示到達（i，j）位置時的不同路徑數
2. 因為只能向下或向右走，因此當前位置只能從上面或左邊過來，dp[i][j] = dp[i-1][j] + dp[i][j-1]
3. 初始化：最左邊只能從頭頂過來，最上面只能從右側過來。即：dp[i][0] = 1; dp[0][j] = 1;
4. 順序是從左上角到右下角
5. dp[i][j] = dp[i-1][j] + dp[i][j-1]（i != 0 && j != 0）

	int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for(int i = 0; i < m; i++) for(int j = 0; j < n; j++) {if(i == 0 || j == 0)dp[i][j] = 1;else dp[i][j] = dp[i-1][j] + dp[i][j-1];}return dp[m-1][n-1];}

方法二：滾動數組,沒太理解，二刷再看

	int uniquePaths(int m, int n) {vector<int> dp(n);for (int i = 0; i < n; i++) dp[i] = 1;for (int j = 1; j < m; j++) {for (int i = 1; i < n; i++) {dp[i] += dp[i - 1];}}return dp[n - 1];}

思路：和上一題區別在于存在障礙物，那么若存在障礙物，dp[i][j] 置為0
還有初始化上的區別：上一題直接 i == 0 || j == 0時，置為1，這次需要判斷當前位置及當前位置以前有沒有障礙，有的話就是0了，所以把初始化這部分單獨拿出來。

	int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起點或終點出現了障礙，直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));dp[0][0] = !obstacleGrid[0][0];for(int i = 1; i < n; i++)dp[0][i] = dp[0][i-1] & !obstacleGrid[0][i];for(int j = 1; j < m; j++)dp[j][0] = dp[j-1][0] & !obstacleGrid[j][0];for(int i = 1; i < m; i++) for(int j = 1; j < n; j++) {if(obstacleGrid[i][j] == 1) {dp[i][j] = 0; } else dp[i][j] = dp[i-1][j] + dp[i][j-1];}// for(int i = 0; i < m; i++) {//     for(int j = 0; j < n; j++) {//         cout << dp[i][j] << " ";//     }//     cout << endl;// }return dp[m-1][n-1];}

看了一下題解，總體思路差不多，但是比我的能簡潔一點，貼出部分代碼：

1. 在初始化dp時，我的做法是全部賦值了，但這里進行了判斷，減少了不必要的賦值操作

	for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;

2. 在循環處理dp數組時，如果當前存在障礙，我又雙叒做了無效賦值操作，直接跳過就好了

	for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}
}

思路：
a(c-a) = -a2 + ac, 在 a = -c(2*-1) 最大，a = c/2;
同理如果是三個 a + b + c = C; a (C-(c+a))(C-(a+b)),好好好不會了
動態規劃上場，所犯不明白為啥要用動態規劃

1. dp[i]：分拆數字i，可以得到的最大乘積為dp[i]。

2. i可以拆成 i-1 + 1 或者 i - 2 + 2, …i-i/2 + i/2;求這個的最大值，即 f[i] = max(f(i-1)*f(1), f(i-2)*f(2), … , f(i-i/2)*f(i/2)); 這感覺和沒有差不多。。。模擬了一下發現還少了一種情況，即當前元素 i > dp[i]，這時應該用當前元素和dp[i]的最大值。f[i] = max(max(f(i-1), i-1)*f(1),

3. 初始化dp數組， dp[1] = 1; dp[2] = 1;

4. 從1~n;

5. 有點推不出來了，看下題解吧

6. i可以拆分為兩個或者多個，如果是兩個那么 dp[i] = max({j, i-j}); 如果是多個，那么 dp[i] = max({j, dp[i-j]}), 使用dp[i] 保存前一次比較結果，即 dp[i] = max(dp[i], j*(i-j), j*dp[i-j]);

    int integerBreak(int n) {vector<int> dp(n+1);dp[2] = 1;for(int i = 3; i <= n; i++) {for(int j = 1; j <= i >> 1; j++) {dp[i] = max(dp[i], max(j * (i-j), j * dp[i-j]));	}	}return dp[n];}

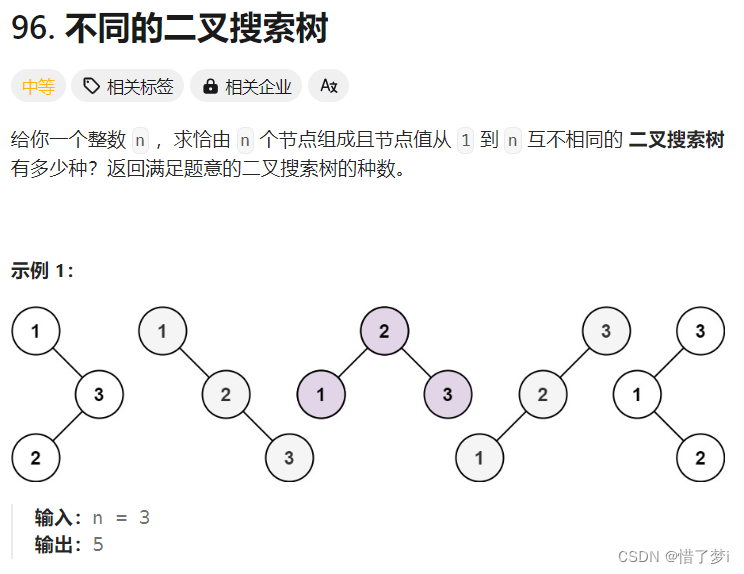
思路：不會，舉例找規律
n = 1 ，1個 0
n = 2, 2個 4
n = 3 5 8
n = 4 14 16
n = 5 42 32
n = 6 132 64
n = 7 429 128