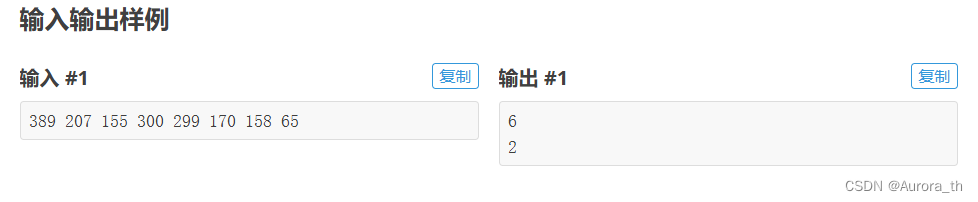
題目描述

某國為了防御敵國的導彈襲擊，發展出一種導彈攔截系統。但是這種導彈攔截系統有一個缺陷：雖然它的第一發炮彈能夠到達任意的高度，但是以后每一發炮彈都不能高于前一發的高度。某天，雷達捕捉到敵國的導彈來襲。由于該系統還在試用階段，所以只有一套系統，因此有可能不能攔截所有的導彈。
輸入導彈依次飛來的高度，計算這套系統最多能攔截多少導彈，如果要攔截所有導彈最少要配備多少套這種導彈攔截系統。

輸入格式

一行，若干個整數，中間由空格隔開。

輸出格式

兩行，每行一個整數，第一個數字表示這套系統最多能攔截多少導彈，第二個數字表示如果要攔截所有導彈最少要配備多少套這種導彈攔截系統。

思路：

首先呢分析一下題目，需要我們求出系統一次最多攔多少枚，其次還需要得出一個把這些導彈全攔下的系統數量的最小值。

第一問

求一次最多攔多少枚，其實就是一個子序列問題，題目說：以后每一發炮彈都不能高于前一發的高度。那就是求最大下降子序列長度唄，這個問題如果學過"LIS"（Longest Increasing Subsequence）那基本第一問在2兩分鐘之內是能出代碼的，沒學過的話可以去了解了解，這個是在計算機科學當中是一個非常常見的概念。

第二問

求系統數量的最小值，這個確實要不好想一些。一般呢遇到這種問題尤其是這個最值他不是很直觀的時候就要想：能不能貪心呢？很明顯是可以的，從頭遍歷數組，維護的一個單調棧，如果指針指向的值小于棧頂直接加入這個棧，如果大于那就去遍歷下一個棧頂，如果全部都加入不了，哎這時候就要再開一個新棧了，最后返回棧的數量就是答案啦

這里我提供兩種方法：

解決

（1）動態規劃

時間復雜度：O（n^2）

代碼

#include <bits/stdc++.h>
using namespace std;const int N = 1e3 + 5;
int a[N],f[N],g[N];int n = 0,ans = 1,res = 1;int main()
{while(cin >> a[n]){f[n] = 1;n ++;}for(int i=n-2;i>=0;i--){for(int j=n-1;j>i;j--){if(a[i] >= a[j]) f[i] = max(f[i],f[j] + 1);}ans = max(ans,f[i]);}cout << ans << endl;g[0] = a[0];for(int i=1;i<n;i++){int k = 0;while(k < res && g[k] < a[i]) k ++;g[k] = a[i];if(k >= res) res ++;}cout << res << endl;return 0;
}

? ?(2)二分

時間復雜度：O（nlogn）

代碼
?

#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 5;
int a[N], dp[N],f[N];int main() {string input;getline(cin, input);stringstream ss(input);int n = 0;while (ss >> a[n]) {n++;}dp[0] = a[0];int cnt = 0,res = 0;for (int i = 1; i < n; i++) {if (a[i] <= dp[cnt]) {dp[++cnt] = a[i];} else {int l = 0, r = cnt;while (l < r) {int mid = (l + r) / 2;if (a[i] > dp[mid]) {r = mid;} else {l = mid + 1;}}dp[l] = a[i];}}cout << cnt + 1 << endl;f[0] = a[0];for(int i=1;i<n;i++){int k = 0;while(k < res && f[k] < a[i]) k ++;f[k] = a[i];if(k >= res) res ++;}cout << res << endl;return 0;
}

我推薦二分，二分比動態規劃好，時間上面是完勝的

加油唄