一、題目
提示:
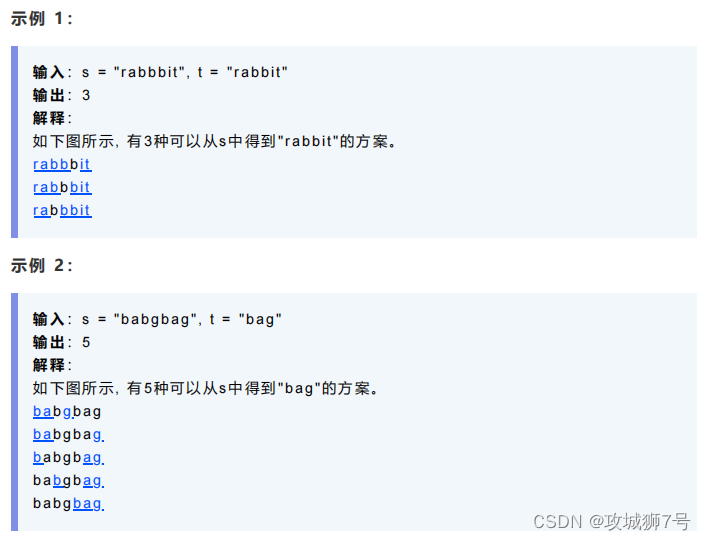
1)0<=s . length, t. length<=1000
2)s和t由英文字母組成
二、求解思路
動態規劃解決思路
????????s的子序列中出現t的個數,其實就是字符串s的所有子序列中,和字符串t完全一樣的有多少個。
????????我們定義dp[i][ j]表示t的前i個字符可以由s的前j個字符組成的個數(也可以說是字符串s 的前j個字符組成的子序列中,和字符串t 的前i個字符組成的字符串一樣的有多少個)。
????????那么最終我們只需要求出dp[tLength][ sLength]即可(其中tLength和sLength分別表示字符串t和s的長度)。
????????如果字符串t的第i個字符和字符串s的第j個字符一樣,如下所示

????????如上圖所示我們可以有兩種選擇。
????????如果字符串t的第i個字符和字符串s的第j個字符不一樣,也就是說字符串s的第j個字符不能匹配字符串t的第i個字符。
????????那么我們只能計算字符串s的前j -1個字符構成的子序列中包含字符串t的前i個字符組成的字符串的個數。
????????動態規劃的三個步驟就是定義狀態,列出遞推公式,找出邊界條件。
詳細過程:
????????我們可以定義二維數組 dp[i][j],其中 dp[i][j] 表示字符串 t 的前 i 個字符可以由字符串 s 的前 j 個字符組成的子序列的個數。這里,i 的取值范圍是 0 到 tLength(包括),j 的取值范圍是 0 到 sLength(包括),并且 tLength 和 sLength 分別是字符串 t 和 s 的長度。
初始化時,我們有:
dp[0][j] = 1,對于所有j(包括j = 0),因為空字符串t是s的任何子序列。dp[i][0] = 0,對于所有i > 0,因為s的空子序列不包含任何字符,所以無法與t的任何非空前綴匹配。
接下來,我們考慮 dp[i][j] 的狀態轉移方程。有兩種情況:
- 如果
t[i-1] == s[j-1](注意字符串索引是從0開始的,所以我們用i-1和j-1來訪問實際字符),那么dp[i][j]可以由dp[i-1][j-1](即t的前i-1個字符與s的前j-1個字符組成的子序列個數)加上dp[i][j-1](即不選擇s[j-1]時,t的前i個字符可以由s的前j-1個字符組成的子序列個數)組成。這是因為我們可以選擇將s[j-1]包含在當前子序列中(如果它與t[i-1]匹配),也可以選擇不包含它。 - 如果
t[i-1] != s[j-1],那么dp[i][j]只能由dp[i][j-1]轉移而來,因為我們不能選擇s[j-1]來匹配t[i-1]。
用數學公式表示狀態轉移方程,我們有:
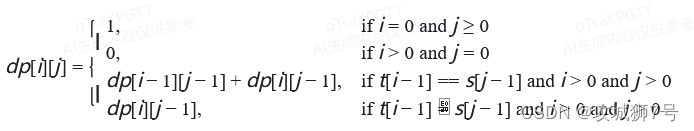
三、代碼實現
C代碼實現
#include <stdio.h>
#include <stdlib.h>
#include <string.h>// 函數 numDistinct 計算字符串 s 中包含字符串 t 作為子序列的不同子序列的數量。
int numDistinct(const char *s, const char *t) {// 獲取兩個字符串的長度int sLength = strlen(s);int tLength = strlen(t);// 為動態規劃表分配內存空間int **dp = (int **)malloc((tLength + 1) * sizeof(int *));for (int i = 0; i <= tLength; i++) {dp[i] = (int *)malloc((sLength + 1) * sizeof(int));memset(dp[i], 0, (sLength + 1) * sizeof(int)); // 初始化為0}// 基礎情況初始化,空字符串是任何字符串的子序列,所以初始化為 1for (int j = 0; j <= sLength; j++) {dp[0][j] = 1;}// 填充動態規劃表for (int i = 1; i <= tLength; i++) {for (int j = 1; j <= sLength; j++) {// 如果 t 的第 i 個字符和 s 的第 j 個字符相同if (t[i - 1] == s[j - 1]) {// 有兩種選擇:// 1. 使用 s[j-1] 來匹配 t[i-1] (dp[i-1][j-1])// 2. 不使用 s[j-1] (dp[i][j-1])dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];} else {// 如果 t 的第 i 個字符和 s 的第 j 個字符不同// 只能選擇不使用 s[j-1]dp[i][j] = dp[i][j - 1];}}}// 保存結果int result = dp[tLength][sLength];// 釋放動態規劃表的內存空間for (int i = 0; i <= tLength; i++) {free(dp[i]);}free(dp);// 返回 t 在 s 中作為子序列出現的總次數return result;
}int main() {const char *s = "rabbbit";const char *t = "rabbit";printf("The number of distinct subsequences is: %d\n", numDistinct(s, t));return 0;
}
在這段代碼中:
- 使用
malloc和memset函數分配和初始化動態規劃表dp的內存。 - 動態規劃表的行
dp[i]表示字符串t的前i個字符在字符串s的前j個字符中作為子序列出現的次數。 - 在計算完成后,使用
free釋放動態規劃表dp的內存。 main函數提供了一個簡單的測試用例來演示函數的使用。
C++代碼實現
#include <vector>
#include <string>// 函數 numDistinct 計算字符串 s 中包含字符串 t 作為子序列的不同子序列的數量。
int numDistinct(const std::string& s, const std::string& t) {// 獲取兩個字符串的長度int sLength = s.length();int tLength = t.length();// 使用 vector 構建二維動態規劃表 dp// dp[i][j] 表示 t 的前 i 個字符可以在 s 的前 j 個字符中出現的次數std::vector<std::vector<int>> dp(tLength + 1, std::vector<int>(sLength + 1, 0));// 基礎情況初始化,空字符串是任何字符串的子序列,所以初始化為 1for (int j = 0; j <= sLength; j++) {dp[0][j] = 1;}// 填充動態規劃表for (int i = 1; i <= tLength; i++) {for (int j = 1; j <= sLength; j++) {// 如果 t 的第 i 個字符和 s 的第 j 個字符相同if (t[i - 1] == s[j - 1]) {// 有兩種選擇:// 1. 使用 s[j-1] 來匹配 t[i-1] (dp[i-1][j-1])// 2. 不使用 s[j-1] (dp[i][j-1])dp[i][j] = dp[i - 1][j - 1] + dp[i][j - 1];} else {// 如果 t 的第 i 個字符和 s 的第 j 個字符不同// 只能選擇不使用 s[j-1]dp[i][j] = dp[i][j - 1];}}}// 返回 t 在 s 中作為子序列出現的總次數return dp[tLength][sLength];
}
在這段代碼中:
std::vector<std::vector<int>> dp創建了一個二維動態數組來存儲中間結果。dp[i][j]表示字符串t的前i個字符在字符串s的前j個字符中作為子序列出現的次數。- 初始化
dp[0][j]為1,因為空字符串是任何字符串的子序列。 - 循環遍歷
t和s,根據當前字符是否匹配,更新dp表。 - 最終返回
dp[tLength][sLength],它包含了t作為s的子序列的出現次數。



:動態規劃——最長公共子序列)

 和 uni.showShareImageMenu({}) 的區別)










指針的一些相關習題講解(速進,干貨滿滿)(2))


)