拓撲排序

拓撲排序要解決的問題是給一個有向無環圖的所有節點排序。

即在$AOE$網中找關鍵路徑。

前置芝士！

• 有向圖：有向圖中的每一個邊都是有向邊，即其中的每一個元素都是有序二元組。在一條有向邊$(u,v)$中，稱$u$是$v$的直接前驅，$v$是$u$的直接后繼。
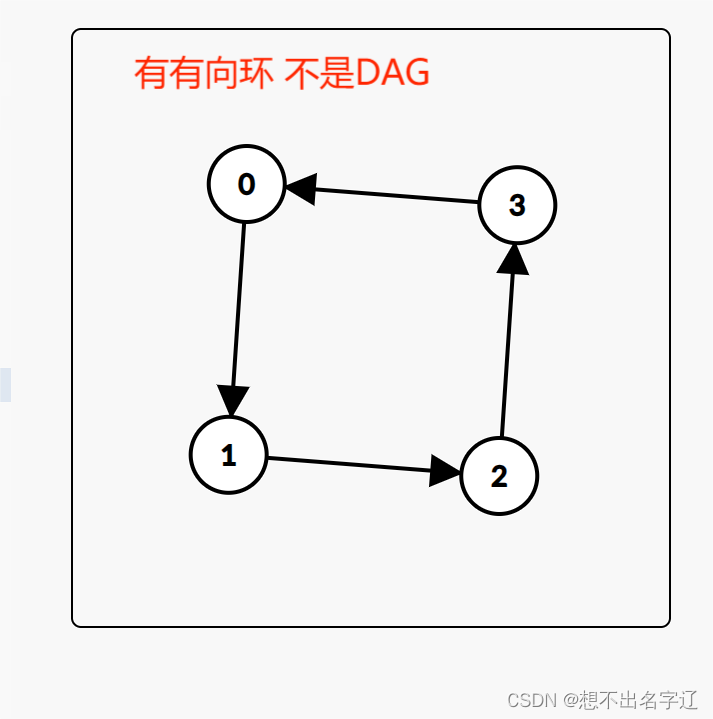
• 有向無環圖$(DirectedAcyclicGraph)$：沒有有向環，但不保證原圖變成無向圖時無環。

• $DAG$的性質：能拓撲的圖一定是$DAG$，$DAG$一定能拓撲。($AOE和AOV$網都是$DAG$)
• 度：頂點$v$的度數是與$v$關聯的邊數。有向圖中沒有度的概念。
• 入度、出度：入度是指以該頂點為終點的有向邊數量；頂點的出度是指以頂點為起點的有向邊數量。無向圖中沒有出入度的概念。

舉個例子！

我們可以拿大學排課的例子來描述這個過程，比如學習大學課程中有：程序設計，算法語言，高等數學，離散數學，編譯技術，數據結構，數據庫系統等。當我們想要學習數據結構的時候，就必須先學會離散數學、編譯技術和算法語言。

這些課程就相當于幾個頂點$u$, 頂點之間的有向邊$(u,v)$就相當于學習課程的順序。教務處安排這些課程，使得在邏輯關系符合的情況下排出課表，就是拓撲排序的過程。

但是如果某一天排課的老師打瞌睡了，說想要學習數據結構，還得先學操作系統，而操作系統的前置課程又是數據結構，那么到底應該先學哪一個（不考慮同時學習的情況）？在這里數據結構和操作系統間就出現了一個環，顯然你現在沒辦法弄清楚你需要先學什么了，于是你也沒辦法進行拓撲排序了。

拓撲排序即，在一個 $DAG$（有向無環圖）中，我們將圖中的頂點以線性方式進行排序，使得對于任何的頂點u到v的有向邊$(u,v)$, 都可以有$u$在$v$的前面。

嚴謹來說，給定一個$DAG$，如果從$i$到$j$有邊，則認為$j$依賴于$i$。如果$i$到$j$有路徑（$i$可達$j$ ），則稱$j$間接依賴于$i$。拓撲排序的目標是將所有節點排序，使得排在前面的節點不能依賴于排在后面的節點。

理論存在！

1. 從圖中選擇一個入度為零的點。
2. 記錄該頂點，從圖中刪除此頂點及其所有的出邊。

重復上面兩步，直到所有頂點都輸出，拓撲排序完成，此時我們可以得到一個點的出隊順序（遍歷順序）這個序列叫拓撲序；或者圖中不存在入度為零的點，此時說明圖是有環圖，拓撲排序無法完成。

拓撲排序需要遍歷整張圖，假設該圖為$G(V,E)$，獲得拓撲序的時間復雜度大約是O（V+E）。

實踐開始！

void topu_sort() {queue<int>q;for (int i = 1; i <= n; ++i) {if (!d[i])q.push(i);}while (!q.empty()) {int now = q.front();q.pop();ans.push_back(now);int len = vec[now].size();for (int i = 0; i < len; ++i) {int to = vec[now][i];d[to]--;if (!d[to]) q.push(to);}}/*for(auto x:vec[now]){d[x]--;if(!d[x]) q.push(x);}*/
}

例題

拓撲模板：B3644 【模板】拓撲排序 / 家譜樹 - 洛谷 | 計算機科學教育新生態 (luogu.com.cn)

AC代碼：

#include<bits/stdc++.h>
using namespace std;
const int N = 150;
int n;
vector<int> e[N];
int d[N];
vector<int> ans;void topu() {queue<int> q;for (int i = 1; i <= n; ++i) {if (d[i] == 0) q.push(i);}while (!q.empty()) {int now = q.front();q.pop();ans.push_back(now);for (auto x: e[now]) {d[x]--;if (d[x] == 0) q.push(x);}}
}int main() {cin >> n;for (int i = 1; i <= n; ++i) {int x;while (cin >> x) {if (x == 0) break;d[x]++;e[i].push_back(x);}}topu();for (auto x: ans) {cout << x << " ";}cout << '\n';return 0;
}

提高

拓撲構造：Problem - E - Codeforces

解析：

先忽略所有輸入的無向邊（但是不忽略點），對當前的有向圖拓撲排序，如果給定的有向圖中已經不是$DAG$顯然是一定不成立也無法構造的；如果當前的圖是$DAG$，那么拓撲完我們可以得到一個或多個拓撲序，每個拓撲序都是線性的，這也代表當選定一個拓撲序，在所有點中任選兩個點，他們一定有已知確定先后順序，我們按照這樣的順序去構造，建邊（每次令拓撲序靠前的指向靠后的）即可保證不會出現拓撲序靠前的點依賴于靠后的點，則不會出現有向環。

AC代碼：

pii ans[N];
vector<int>e[N];
int d[N];
int n,m,order=0;
int ord[N];bool topu(){queue<int>q;for(int i=1;i<=n;++i){if(!d[i]){q.push(i);}}while(!q.empty()){int t=q.front();q.pop();ord[t]=++order;for(auto x:e[t]){d[x]--;if(!d[x])q.push(x);}}if(order!=n)return 0;return 1;
}void work() {cin>>n>>m;int tot=0;order=0;for(int i=1;i<=n;++i){d[i]=0;e[i].clear();ans[i].fi=ans[i].se=0;}for(int i=1;i<=m;++i){int z,u,v;cin>>z>>u>>v;if(z){e[u].pb(v);d[v]++;}else{ans[++tot].fi=u;ans[tot].se=v;}}if(!topu()){cout<<"No\n";return;}cout<<"Yes\n";for(int i=1;i<=tot;++i){if(ord[ans[i].fi]>ord[ans[i].se])swap(ans[i].se,ans[i].fi);cout<<ans[i].fi<<" "<<ans[i].se<<'\n';}for(int i=1;i<=n;++i){if(e[i].size()){for(auto x:e[i]){cout<<i<<" "<<x<<'\n';}}}
}

課后練習：P1347 排序 - 洛谷 | 計算機科學教育新生態 (luogu.com.cn)

總結：

拓撲排序是圖論中非常基礎的算法，大多時候作為工具，或者一些進階算法的預處理內容，非常簡單，同時需要熟練掌握。