(內容源自詳解MATLAB/SIMULINK 通信系統建模與仿真?? 劉學勇編著第三章內容,有興趣的讀者請閱讀原書)
一、求離散信號卷積和
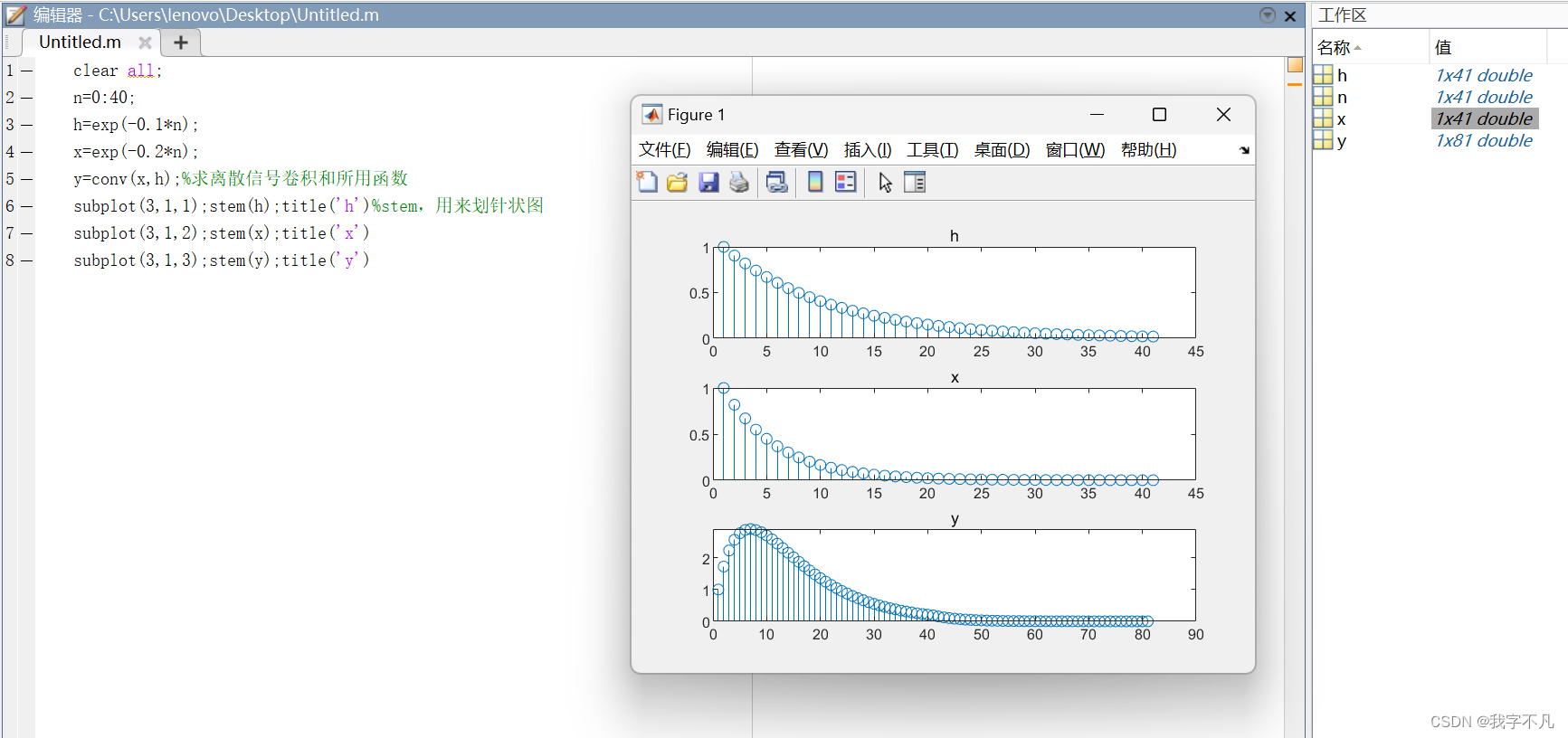
主要還是使用卷積函數conv,值得注意的是,得到的卷積和長度結果為81,是兩個原始序列長度相加-1(41+41-1);
?二、連續時間信號的傅里葉變換

使用函數fourier和函數ifourier進行傅里葉變換和傅里葉變換,可以注意到,將變量符號化后可以直接得到傅里葉變換后的數學表達式。
clear all;
syms t;%調用函數fourier和ifourier需要使用syms命令對涉及到的變量進行說明,將其說明為符號變量
f=t*exp(-abs(t));
subplot(1,2,1);ezplot(f);%函數fourier和ifourier得到的返回函數仍然是符號表達式,作圖應使用ezplot函數(有沖激函數ezplot無法使用)
F=fourier(f)
subplot(1,2,2);ezplot(abs(F));%abs(F)用來做幅頻特性的圖像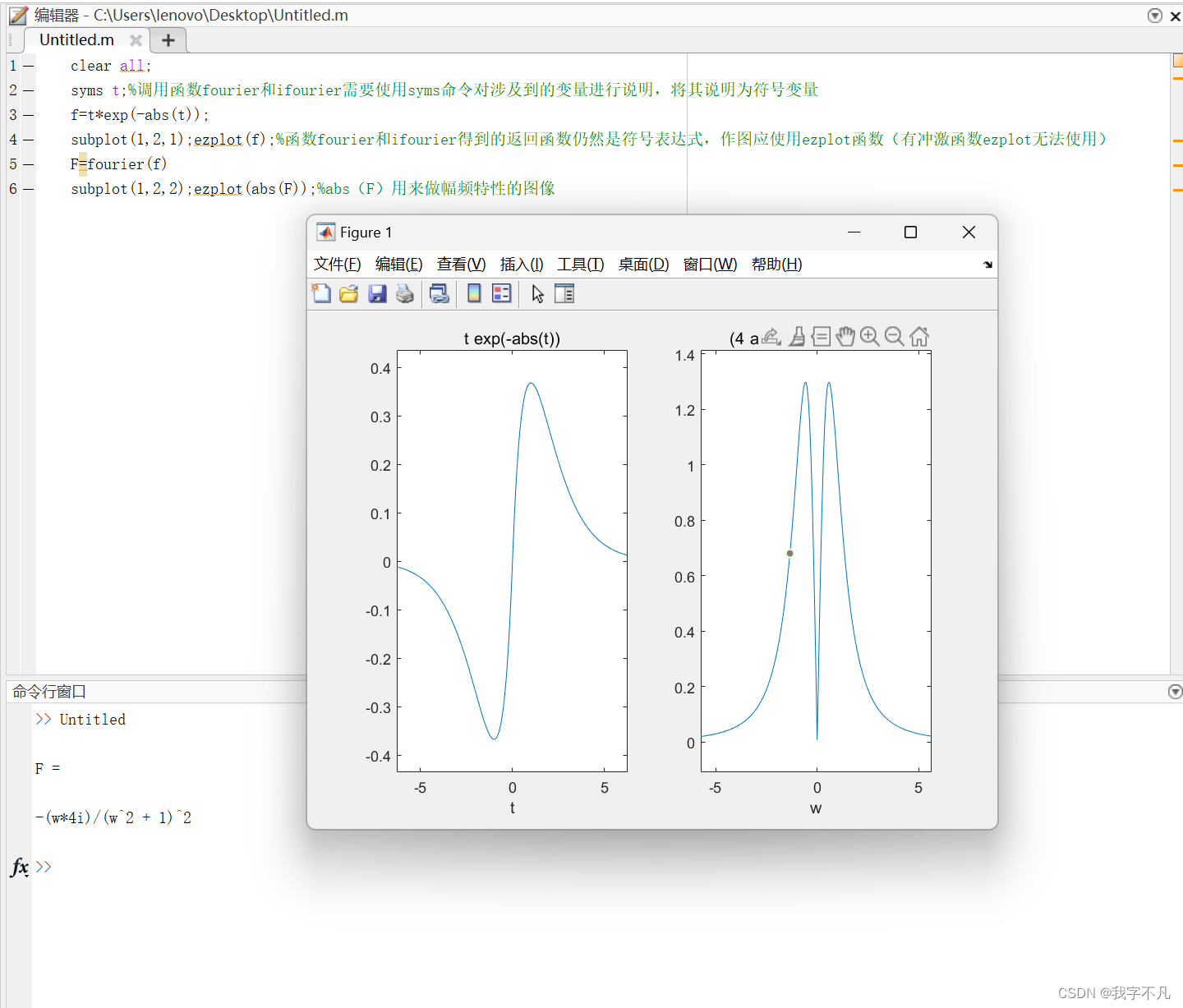
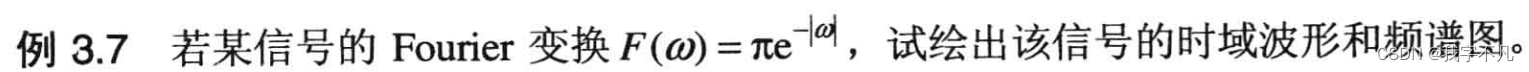
clear all;
syms t w;%在反變換中涉及到了t和w兩個變量,都需要符號化
F=pi*exp(-abs(w));
subplot(1,2,1);ezplot(abs(F));%頻譜圖
f=ifourier(F,t)%ifourier默認返回是關于x的函數,這里指定為返回t的函數
subplot(1,2,2);ezplot(f);%時域圖

?此題中是周期信號,不可積分,所以無法使用傅里葉變換,所以采用傅里葉級數進行求解

?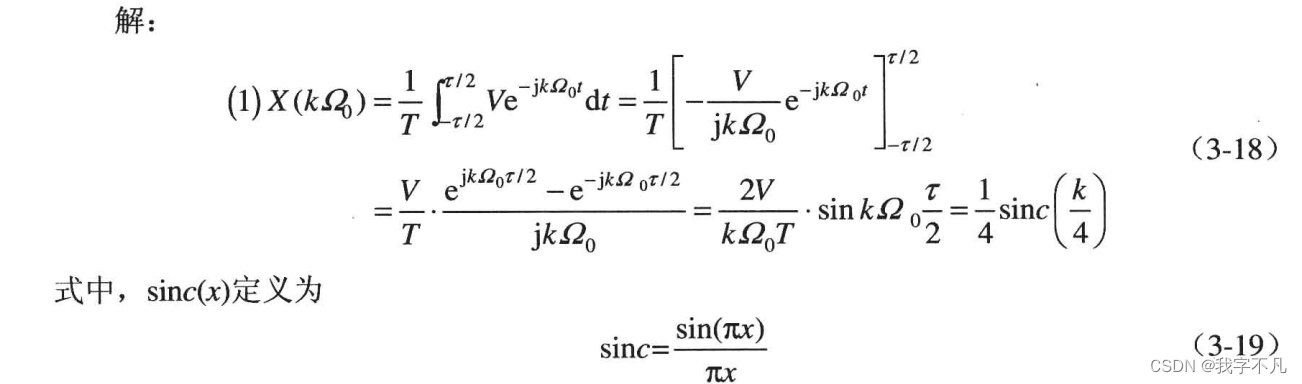
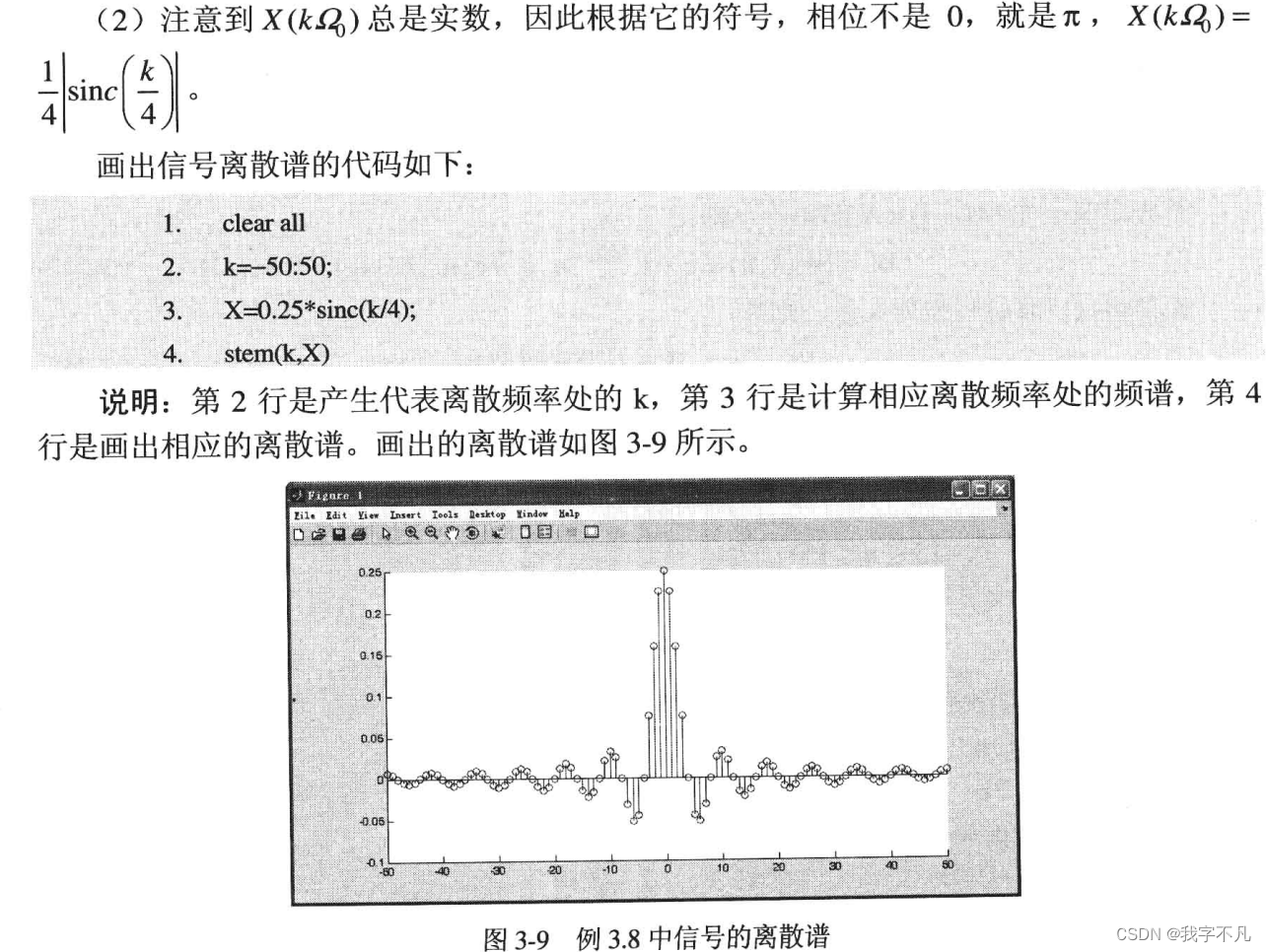
這題中我們是使用手動積分算出傅里葉級數的表達式后直接對表達式進行畫圖的,個人理解是因為無窮長的信號在matlab中表示較為復雜,所以反而是手動求解更快。
三、離散時間信號的傅里葉變換


clear all;
w=-1:0.001:1;%產生數字頻率的范圍,這里的單位長度是pi,所以只計算了[-pi,pi]范圍內的DTFT
n=0:20;%離散序列的時間范圍,0<n<20;
h(n+1)=1;%構造信號h(n)=1,這里n+1的理由是matlab數組都是從1開始計算的,數組索引必須為正整數或邏輯值。
x=h.*exp(j*pi*n/4);%構造信號x(n);
Hjw=h*(exp(-j*pi).^(n'*w));%dtft公式,這里n'*w是利用數字頻率和時間范圍構造了一個矩陣,之后將矩陣與-j*pi
%相乘后進行exp運算,最后將表達式與數字序列相乘,得到數字序列的DTFT值
Xjw=x*(exp(-j*pi).^(n'*w));
subplot(2,2,1);plot(w,abs(Hjw));
title('H');xlabel('pi弧度(w)');ylabel('振幅')
subplot(2,2,2);plot(w,angle(Hjw/pi));%用angle繪制相位圖,除以pi是因為以pi弧度為單位的
title('H');xlabel('pi弧度(w)');ylabel('相位')
subplot(2,2,3);plot(w,abs(Xjw));
title('H');xlabel('pi弧度(w)');ylabel('振幅')
subplot(2,2,4);plot(w,angle(Xjw/pi));
title('H');xlabel('pi弧度(w)');ylabel('相位')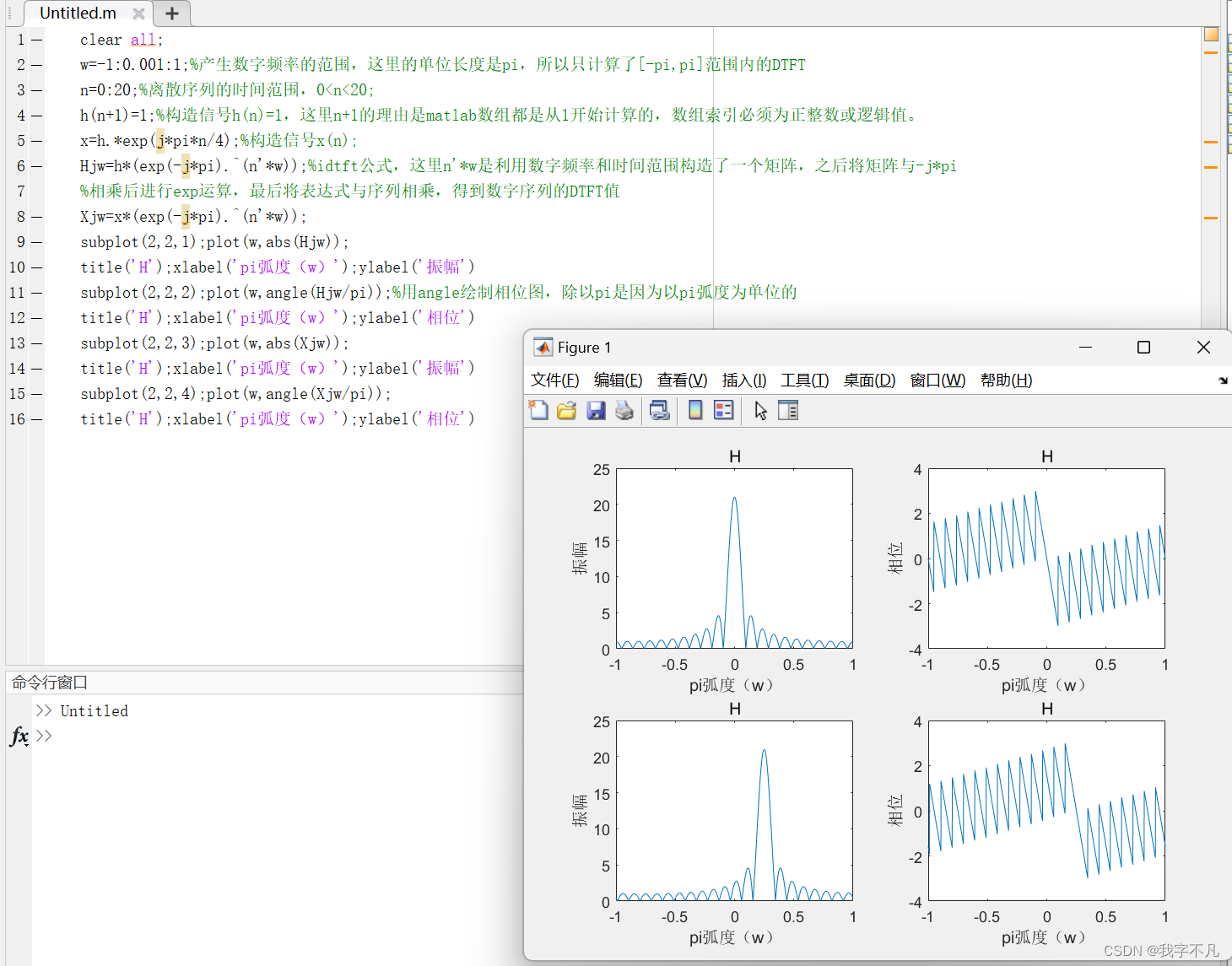
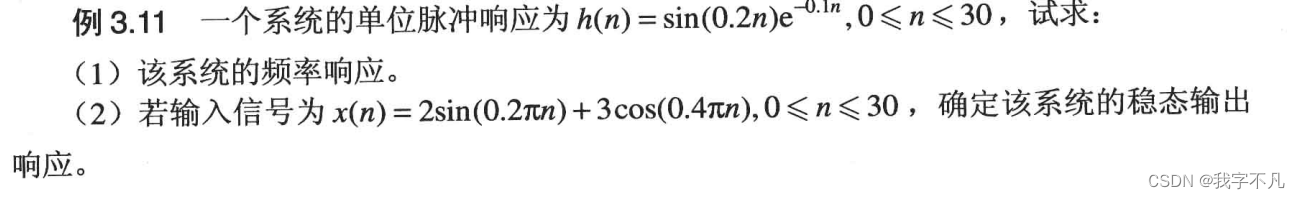
clear all;
w=-1:0.001:1;%產生數字頻率的范圍,這里的單位長度是pi,所以只計算了[-pi,pi]范圍內的DTFT
n=0:30;%離散序列的時間范圍,0<n<30;
h=sinc(0.2*n);
x=2*sin(0.2*pi*n)+3*cos(0.4*pi*n);
Hjw=h*(exp(-j*pi).^(n'*w));
Xjw=x*(exp(-j*pi).^(n'*w));
Yjw=Xjw.*Hjw;%這里是第一種方法,通過DTFT求出x和h信號的傅里葉變換然后相乘,得到了輸出響應y的頻域表達
n1=0:2*length(n)-2;%這里卷積之后的長度等于用于卷積的序列長度相加-1(n+n-1)
dw=0.001*pi;%確定分段求和的步長
y=(dw*Yjw*(exp(j*pi).^(w'*n1)))/(2*pi);%通過y的頻域表達得到y的時域表達,需要用到IDTFT,由于IDTFT公式中用到了積分,這里使用
%分段求和代替積分,步長等于相鄰頻域的間隔,因為w=-1:0.001:1;,所以步長是0.001*pi。求和中和DTFT思路一致,都是用w'*n1
%兩個參數構造的矩陣實現的y1=conv(x,h);%這是第二種方法,時域卷積,第一種是頻域相乘,總結來說,就是時域卷積等價于頻域相乘。
subplot(3,1,1);plot(w,abs(Hjw));
title('H');xlabel('pi弧度(w)');ylabel('振幅');
subplot(3,1,2);plot(w,abs(Xjw));
title('X');xlabel('pi弧度(w)');ylabel('振幅');
subplot(3,1,3);plot(w,abs(Yjw));
title('Y');xlabel('pi弧度(w)');ylabel('振幅'); figure
subplot(2,1,1);stem(abs(y));title('通過IDTFT計算出的輸出序列Y');
subplot(2,1,2);stem(abs(y1));title('通過時域卷積計算出的輸出序列Y1');
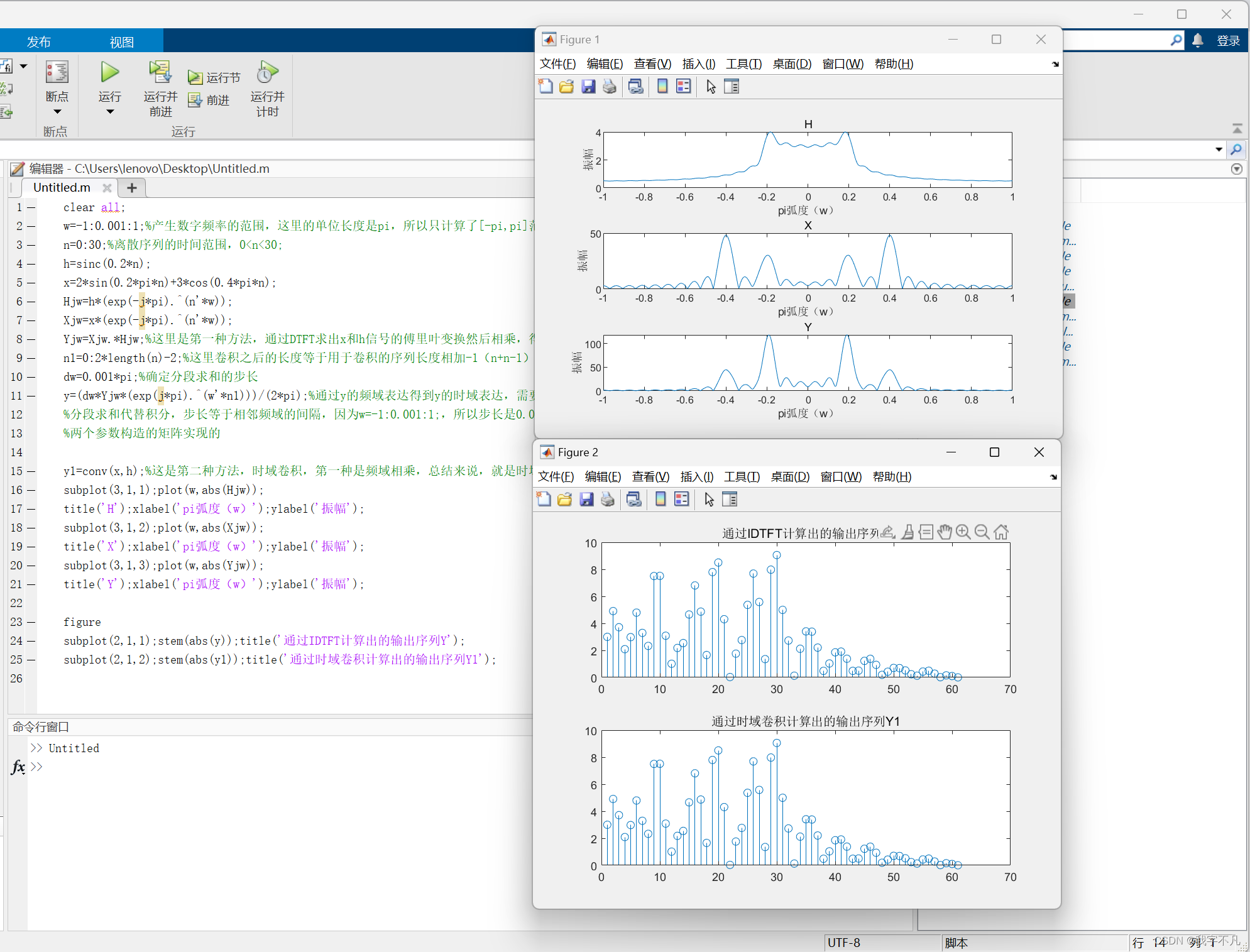
這里有一個有意思的點,就是第9行的n1是從0開始的,但是在例3.10中的第4行h(n+1)中n+1是從1開始的,這是因為h(n+1)中是明確把n+1當做h的索引值了,只有正整數才能作為數組的索引值,而本例中只有利用n進行乘法運算,沒有當做索引值,所以可以從0開始。
,阿里云短信驗證碼)
)













)
單例模式)


