今天下起了暴雨，本以為下午就可以結束的答辯又因為老師開會被推遲。研三的學長走了后我們開始了0元購，收獲頗豐哈哈，做個題

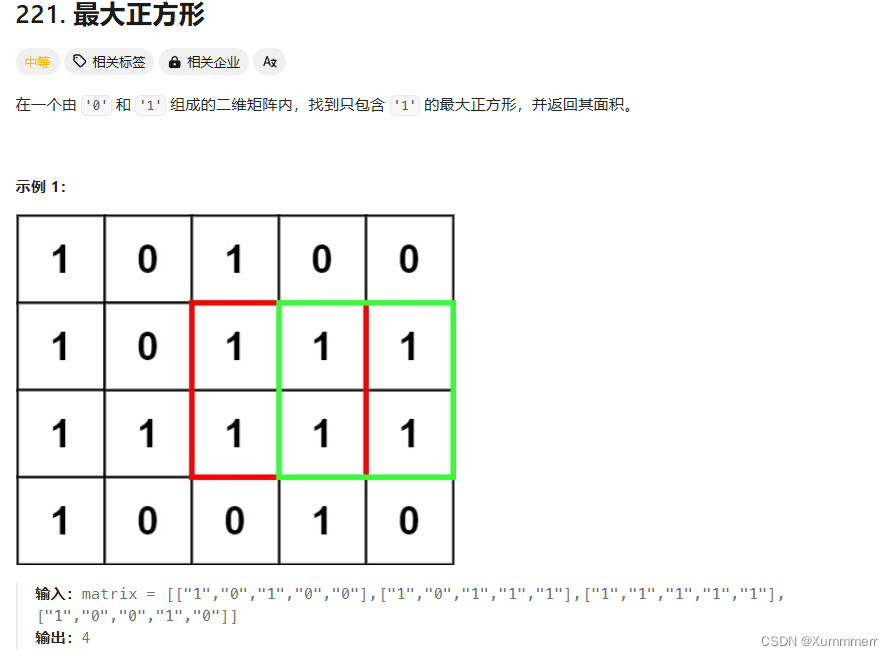
1、題目描述

2、算法分析

給定一個矩形，要求最大正方形。第一次見這種題目哈
2024 6/30 嘿嘿，這道題我昨天沒做啦，今天來做，今天中午就待實驗室啦，回去太麻煩了。那么繼續開始做題
我拿到這個題大概知道跟動態規劃有關，然后看了題解，題解給出兩種算法：暴力與DP。那么我們先來看看暴力解法
暴力法是最簡單直觀的做法，具體做法如下：

1. 遍歷矩陣中的每個元素，每次遇到 1，則將該元素作為正方形的左上角；
2. 確定正方形的左上角后，根據左上角所在的行和列計算可能的最大正方形的邊長（正方形的范圍不能超出矩陣的行數和列數），在該邊長范圍內尋找只包含 1 的最大正方形；
3. 每次在下方新增一行以及在右方新增一列，判斷新增的行和列是否滿足所有元素都是 1。

代碼演示：

public int maximalSquare(char[][] matrix) {// 初始化最大正方形的邊長為0 int maxSide = 0;// 如果矩陣為空，則直接返回0if(matrix == null || matrix.length == 0 || matrix[0].length == 0){return maxSide;}// 獲取矩陣的行數和列數int rows = matrix.length, columns  = matrix[0].length;// 遍歷矩陣中的每個元素  for(int i = 0; i < rows; i++){for(int j = 0; j < columns ; j++){// 如果當前元素是'1'，則開始嘗試以當前位置為左上角的最大正方形的邊長if(matrix[i][j] == '1'){// 更新maxSide，因為至少可以形成一個邊長為1的正方形maxSide = Math.max(maxSide, 1);// 計算當前位置可能形成的最大正方形的最大可能邊長  // 不能超過矩陣的邊界 int currentMaxSide = Math.min(rows - i, columns  - j );// 嘗試從邊長為1開始，逐漸擴大正方形的邊長for(int k = 1; k < currentMaxSide; k++){// 假設當前邊長k的正方形是可能的boolean flag = true;// 檢查正方形的右下角是否為'0'，如果是，則無法形成邊長為k的正方形if(matrix[i + k][j + k] == '0'){break;}// 檢查正方形的右側和下方的邊界是否都為'1'  // 如果有任何一個為'0'，則無法形成邊長為k的正方形for(int m = 0; m < k; m++){if(matrix[i + k][j + m] == '0' || matrix[i + m][j + k] == '0'){flag = false;break;}}// 如果能形成邊長為k的正方形，則更新maxSideif(flag){maxSide = Math.max(maxSide, k + 1);// 如果不能形成邊長為k的正方形，則無需繼續嘗試更大的邊長}else{break;}}}}}// 計算最大正方形的面積并返回int maxSquare = maxSide * maxSide;return maxSquare;}

暴力解法的時間復雜度：$O(mn\min (m,n{)}^2)$，其中 m 和 n 是矩陣的行數和列數。空間復雜度：O(1)。額外使用的空間復雜度為常數。

可以看到空間復雜度很高了，那么我們來看看動態規劃是怎么解決的。

可以使用動態規劃降低時間復雜度。

• 我們用 dp(i,j) 表示以 (i,j) 為右下角，且只包含 1 的正方形的邊長最大值。如果我們能計算出所有
  dp(i,j) 的值，那么其中的最大值即為矩陣中只包含 1 的正方形的邊長最大值，其平方即為最大正方形的面積。
• 那么如何計算 dp 中的每個元素值呢？對于每個位置 (i,j)，檢查在矩陣中該位置的值：
• 如果該位置的值是 0，則 dp(i,j)=0，因為當前位置不可能在由 1 組成的正方形中；
• 如果該位置的值是 1，則 dp(i,j) 的值由其上方、左方和左上方的三個相鄰位置的 dp值決定。具體而言，當前位置的元素值等于三個相鄰位置的元素中的最小值加 1，狀態轉移方程如下：

dp(i,j) = min(dp(i ? 1,j), dp(i ? 1,j ? 1), dp(i,j ? 1) ) + 1

此外，還需要考慮邊界條件。如果 i 和 j 中至少有一個為 0，則以位置 (i,j) 為右下角的最大正方形的邊長只能是 1，因此 dp(i,j)=1。

3、代碼

public int maximalSquare(char[][] matrix) {// 初始化最大正方形的邊長為0int maxSide = 0;// 如果矩陣為空，或者沒有行或列，則直接返回0if(matrix == null || matrix.length == 0 || matrix[0].length == 0){return maxSide;}// 獲取矩陣的行數和列數int rows = matrix.length, columns = matrix[0].length;// 創建一個與原始矩陣大小相同的二維dp數組，用于存儲每個位置的最大正方形邊長int[][] dp = new int[rows][columns];// 遍歷矩陣的每一個位置for(int i = 0; i < rows; i++){for(int j = 0 ; j < columns; j++){// 如果當前位置是'1' if(matrix[i][j] == '1'){// 如果當前位置是第一行或第一列，則最大正方形邊長只能是1 if(i == 0 || j == 0){dp[i][j] = 1;}else{// 否則，當前位置的最大正方形邊長取決于其上方、左方和左上方的最小邊長，并加1  // 因為我們要考慮的是由'1'組成的正方形dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;}// 更新最大正方形的邊長maxSide = Math.max(maxSide, dp[i][j]);}               }}// 計算最大正方形的面積（邊長的平方）int maxSquare = maxSide * maxSide;// 返回最大正方形的面積return maxSquare;}

這里的dp思想跟我之前做的一道最短路徑思想是一樣的。通過填充一個與原始矩陣大小相同的dp數組來記錄每個位置的最大正方形邊長。最終，返回的是最大正方形的面積，而不是邊長。

4、復雜度分析

• 時間復雜度：O(mn)，其中 m 和 n 是矩陣的行數和列數。需要遍歷原始矩陣中的每個元素計算 dp 的值。
• 空間復雜度：O(mn)，其中 m 和 n 是矩陣的行數和列數。創建了一個和原始矩陣大小相同的矩陣 dp。由于狀態轉移方程中的 dp(i,j) 由其上方、左方和左上方的三個相鄰位置的 dp 值決定，因此可以使用兩個一維數組進行狀態轉移，空間復雜度優化至 O(n)。