[導讀]：超平老師的Scratch藍橋杯真題解讀系列在推出之后，受到了廣大老師和家長的好評，非常感謝各位的認可和厚愛。作為回饋，超平老師計劃推出《Python藍橋杯真題解析100講》，這是解讀系列的第89講。

小馬搬運物品，本題是2022年4月23日舉辦的第13屆藍橋杯青少組Python編程省賽真題編程部分第4題，13屆一共舉辦了兩次省賽，這是第二次省賽。題目要求編程計算小馬將N件物品從河的一岸搬運到河的另一岸一共有多少種方案。

先來看看題目的要求吧。

一.題目說明

時間限制：3000MS

內存限制：589824K8

編程實現：

小馬需要將N件物品從河的一岸搬運到河的另一岸，每次搬運的物品為1到3件。請問小馬將N件物品全部搬運過去有多少種方案。

例如：N = 3，將3件物品全部搬運過去有4種方案：

方案一：第一次搬運1件，第二次搬運1件，第三次搬運1件；

方案二：第一次搬運1件，第二次搬運2件；

方案三：第一次搬運2件，第二次搬運1件；

方案四：一次搬運3件。

輸入描述：

輸入一個正整數N，表示需要搬運的物品數

輸出描述：

輸出將N件物品全部搬運過去有多少種方案

樣例輸入:

3

樣例輸出：

4

評分標準：

• 10分：能正確輸出一組數據；

• 10分：能正確輸出兩組數據；

• 20分：能正確輸出三組數據；

• 20分：能正確輸出四組數據。

二.思路分析

這是一道經典的算法題，涉及的知識點包括循環、條件、列表、遞歸、動態規劃等。

看完題目描述，你腦海里首先想到的是什么呢？

如果你想到的是斐波那契數列，那么恭喜你，這道題基本上就可以拿下了。

實際上，這是斐波那契數列的變種問題。

對于經典的斐波那契數列來說，每一項（第1項和第2項除外）都只和前面的兩項有關系，即：

f(n)?=?f(n?-?1)?+?f(n?-?2)

本題中小馬的搬運方案，每一項（前面3項除外）都和前面的三項有關系，如下：

f(n)?=?f(n?-?1)?+?f(n - 2) + f(n - 3)

這是怎么推導出來的呢？

對于這種具有遞推性質的問題，通常只需要考慮最后一步是如何計算的，就可以迅速的確定推導公式。

我們使用f(n)表示搬運n件物品的方案數量，最后一次到底搬運幾件物品呢？

可以分3種情況討論：

• 搬運3件物品，那么搬運n - 3件物品的方案數為f(n - 3)；

• 搬運2件物品，那么搬運n - 2件物品的方案數為f(n - 2)；

• 搬運1件物品，那么搬運n - 1件物品的方案數為f(n - 1)；

根據加法原理，當完成一件事情有n種不同的方式，且這些方式之間互不影響，那么完成這件事情的總方法數就是各類方式中的方法數之和。

因此，總的方案數量f(n)就等于f(n - 1)?+ f(n - 2) + f(n - 3)。

對于斐波那契數列及其變種這類問題，通常有如下三種解決方案：

• 遞歸算法

• 動態規劃

• 遞推算法

不管使用哪一種思路，都需要單獨考慮邊界問題，對于本題而言，需要考慮前3項。

如果只有一件物品，毫無疑問只有一種方法，即f(1) = 1。

如果有兩件物品，可以一次搬運兩件，也可以分兩次，每次搬運一件，所以一共有兩種方案，即f(2) = 2。

如果有三件物品，可以每次搬運一件，分3次搬運，也可以一次搬運3件，還可以第一次搬運1件，第二次搬運2件，又或者是第一次搬運2件，第二次搬運1件，一共有4種方案，即f(3) = 4。?

思路有了，接下來，我們就進入具體的編程實現環節。

三.編程實現

根據上面的思路分析，我們分別使用3種方案來編寫程序：

• 遞歸算法

• 動態規劃

• 遞推算法

1. 遞歸算法

遞歸算法的重點是定義遞歸函數，代碼如下：

代碼比較簡單，但是隨著n的增加，代碼運行的時間會越來越長，效率會急劇下降。

其原因在于存在大量重復的計算，可以增加一個備忘錄將每一次的計算結果保存起來，避免重復計算。

使用帶備忘錄的遞歸代碼如下：

代碼不多，強調一點，這里的memo列表就是備忘錄，前3項不需要保存，從第4項開始保存，對應于memo[4]。

有了備忘錄，算法效率大大提高。

2. 動態規劃

這里的推導公式（狀態轉移方程）和初始狀態都已經確定好了，代碼就比較簡單了，如下：

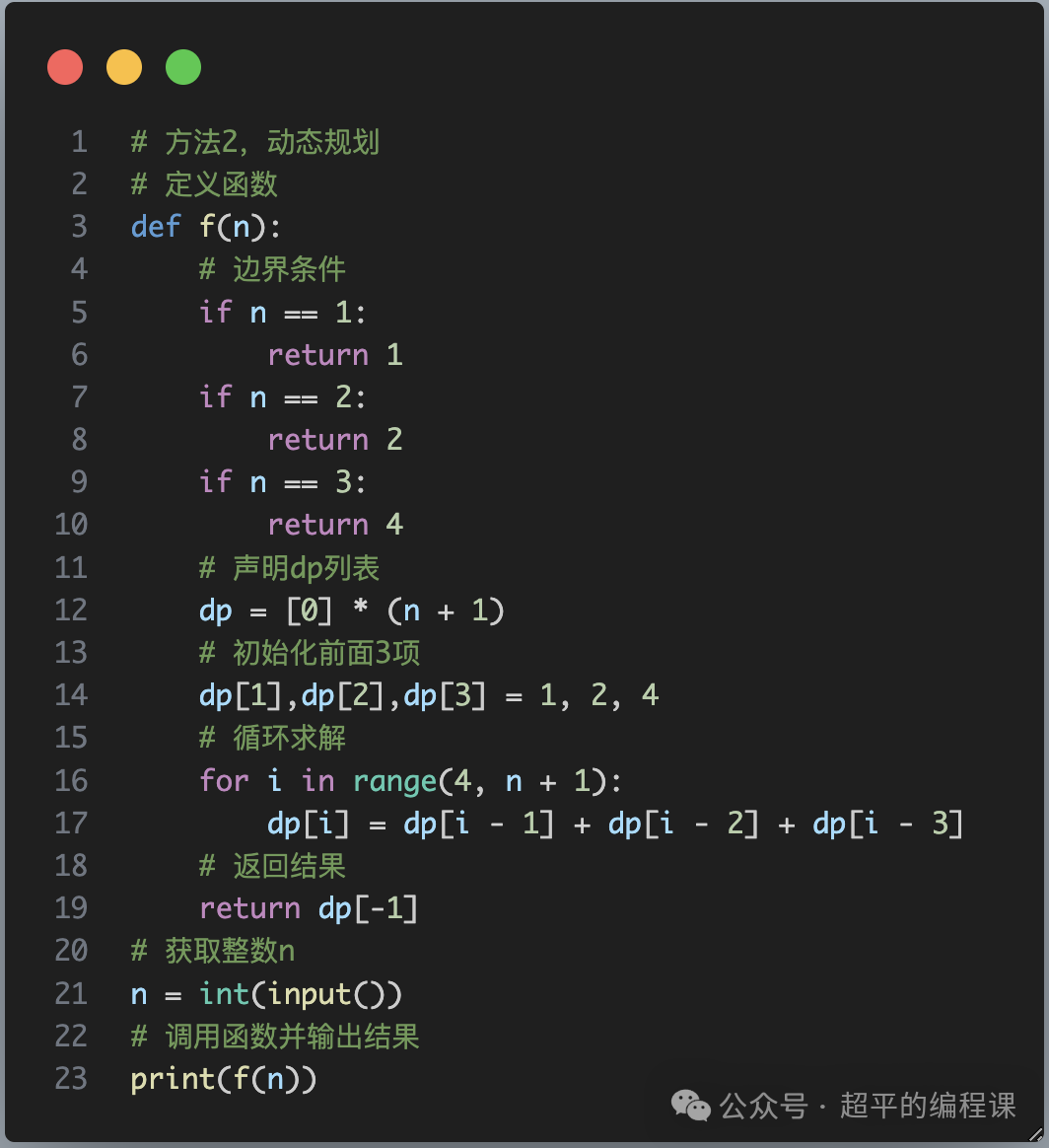
代碼并不多，說明4點：

1). 這里定義函數f(n)用于計算搬運n件物品的方案數量，主要是為了方便處理邊界條件，但它不是遞歸函數；

2). Python支持多變量賦值運算，因此可以直接寫成dp[1], dp[2], dp[3] = 1, 2, 4，代碼看起來更加緊湊；

3). 在循環計算的時候，從第4項開始，所以range()函數的起點是4；

4). dp列表的最后一項就是要計算的方案數量，可以使用dp[n]獲取，也可以使用dp[-1]獲取。

3. 遞推算法

針對上面的動態規劃算法，仔細想一想，每一項只和前3項有關，是不是只要保存這3項就可以了呢？

答案是肯定的，只需要4個變量就夠了，1個表示當前項，另外3個用來保存前3項，從而節省了一個列表，這就是遞推的寫法，也叫迭代，代碼如下：

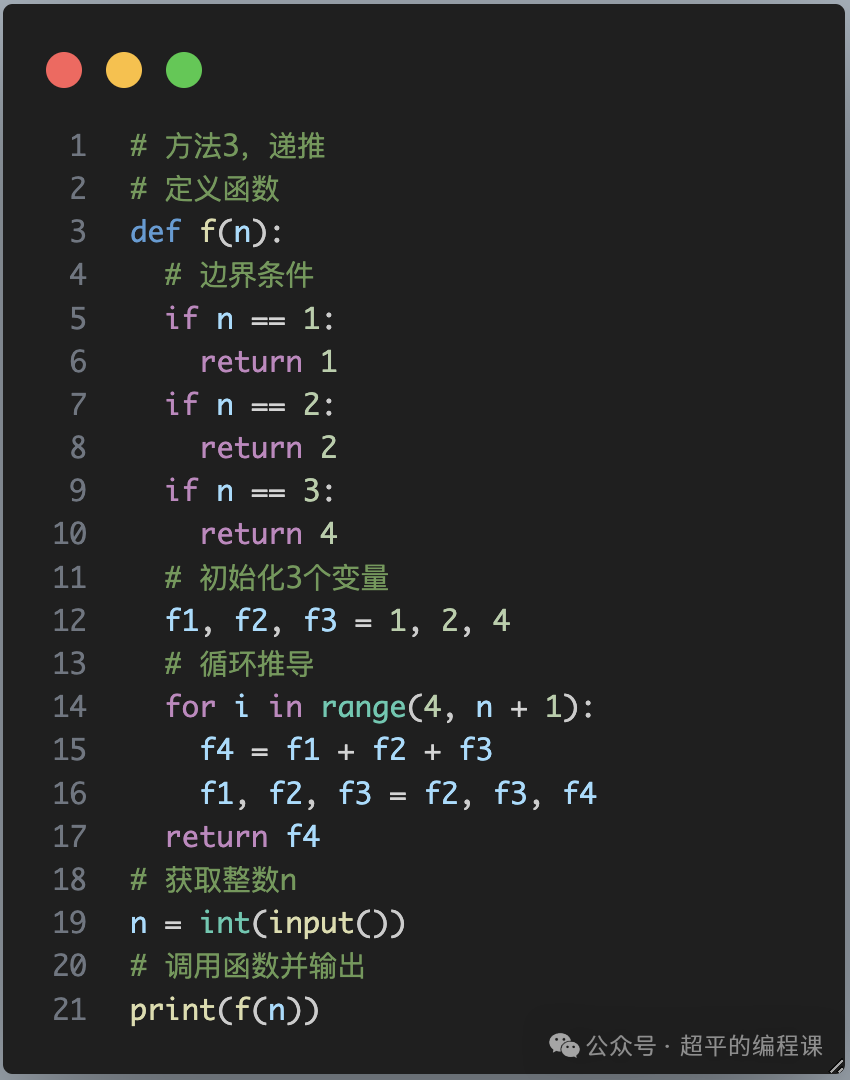
代碼不難，強調一點，由于每一次都需要保存最后3項，需要不斷更新f1，f2，f3的值，這就是f1, f2, f3 = f2, f3, f4的作用。

至此，整個程序就全部完成了，你可以輸入不同的數據來測試效果啦。

四.總結與思考

本題代碼在14行左右，涉及到的知識點包括：

• 循環語句；

• 條件語句；

• 列表；

• 遞歸算法；

• 動態規劃函數；

• 遞推算法；

本題分值為60分，難度中等。關鍵點有兩個，一是找到搬運物品方案的規律，確定好推導公式，二是使用多種算法來實現。

在找規律確定推到公式的問題時，一定要學會運用遞歸思維，將問題簡化為兩個步驟。最后一步保留，最后一步之前的所有步驟當作一步，然后看最后一步是如何計算出來的。切不可小瞧了這一點，在編程中，有很多問題都可以使用這一思維來解決。

本教程講解了3種解決方案，這3種方案絕不是孤立的，它們之間都有一個共同的觀點，這就是推導公式。

實際上，凡是有推導公式的問題，基本上可以采用這3種算法，尤其是帶備忘錄的遞歸和動態規劃。如果說遞歸是自頂向下的推導過程，那么動態規劃就是自底向上的推導過程。

和斐波那契數列相關的題目在歷屆真題中多次出現，如下：

• 《病毒繁殖-第12屆藍橋杯選拔賽Python真題精選》

• 《密室逃脫游戲-第12屆藍橋杯省賽Python真題精選》

• 《跳房子游戲-第13屆藍橋杯選拔賽Python真題精選》

你可以放在一起來分析對比，以加深理解。

你還有什么好的想法和創意嗎，也非常歡迎和超平老師分享探討。

如果你覺得文章對你有幫助，別忘了點贊和轉發，予人玫瑰，手有余香😄

需要源碼的，可以移步至“超平的編程課”gzh。