原視頻鏈接：attention

一. 基本問題分析

1. 模型的input

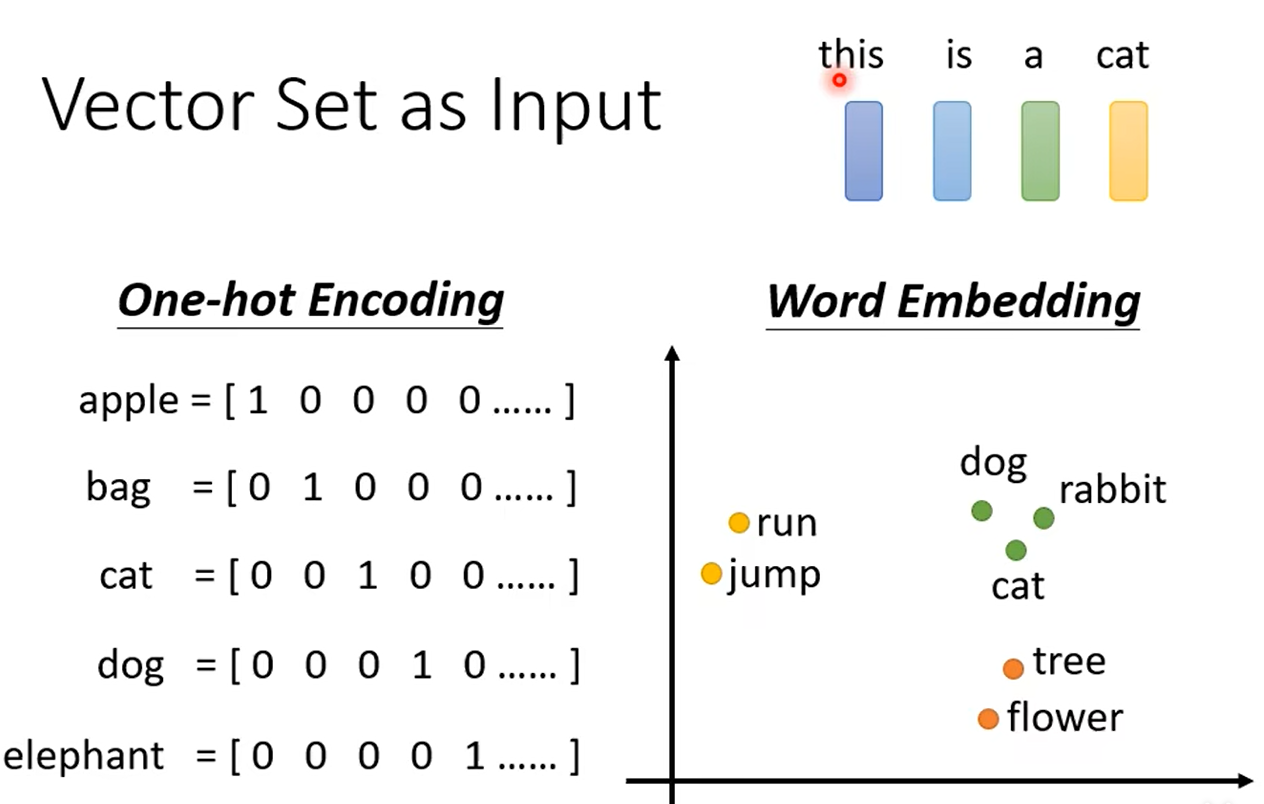
無論是預測視頻觀看人數還是圖像處理，輸入都可以看作是一個向量，輸出是一個數值或類別。然而，若輸入是一系列向量，長度可能會不同，例如把句子里的單詞都描述為向量，那么模型的輸入就是一個向量集合，并且每個向量的大小都不一樣。解決這個問題的方法是One-hot Encoding以及Word Embedding，其中Word Embedding更能考慮到相似向量的語義信息，如下所示：

2. 模型的output

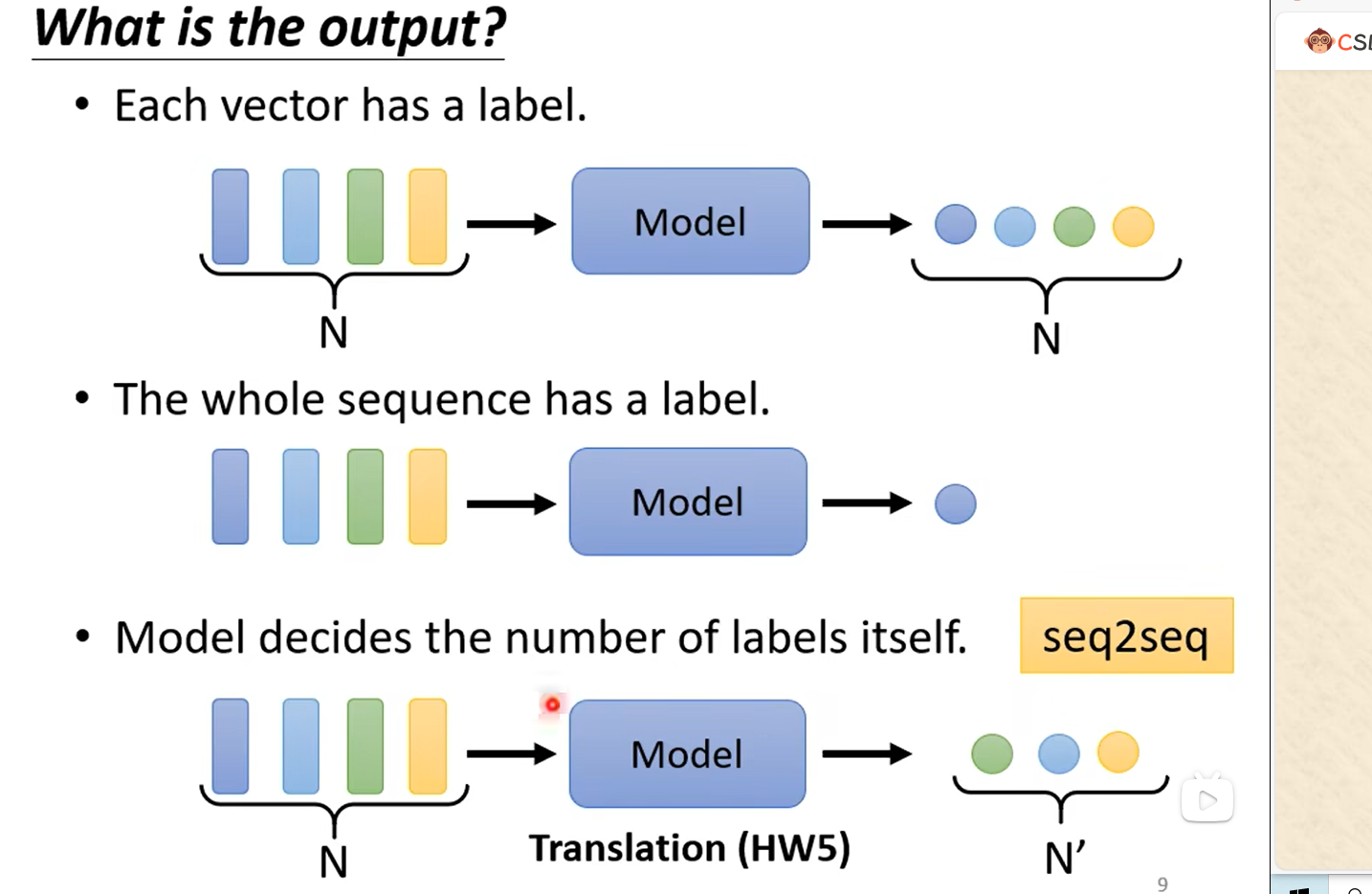
輸出可以是每個vector都產生個對應的label，即N to N。如：在社交網絡中，推薦某個用戶商品（這個用戶可能會買或者不買）；

也可以是N to 1。如：情感分析，給出一句話this is good，輸出positive；反之給出另一段消極的話輸出negative；

也可以是N to M。如：翻譯工作，翻譯到另一個語言可能和原語言單詞長度不一樣

3. attention的引入

比如我們想利用全連接網絡，輸入一個句子，輸出對應單詞的標簽。當一個句子里出現兩個相同的單詞，并且它們的詞性不同（例如：I saw a saw. 我看見一把鋸子），這個時候就需要考慮上下文：利用滑動窗口，每個向量查看窗口中相鄰的其他向量的性質。?但是滑動窗口所觀看的視野是有限的，窗口增大又會計算量增大，且容易過擬合，這就引出了self-attention機制。

二. self-attention機制

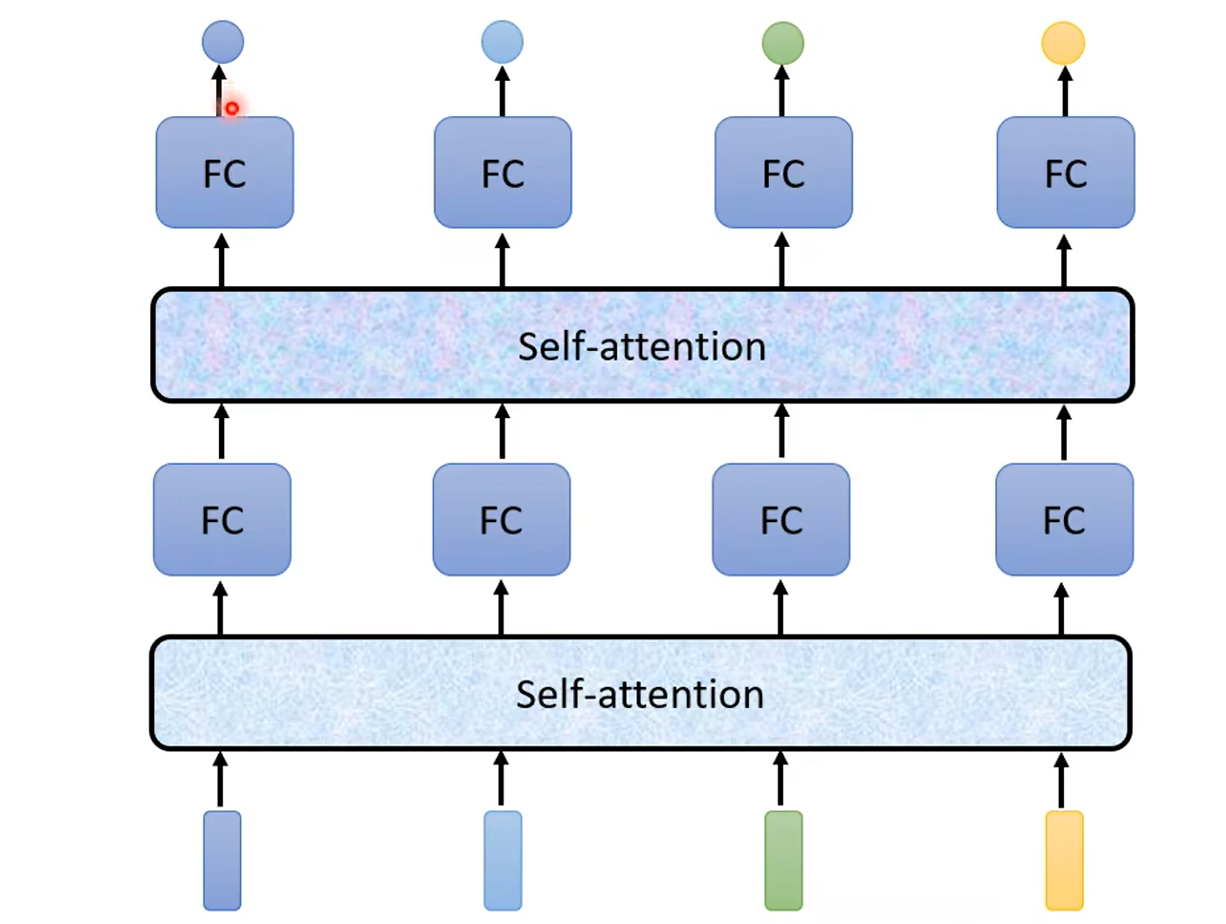
輸入整個語句的向量到self-attention中，輸出對應單詞的向量，再將其結果輸入到全連接網絡，最后輸出標簽。以上過程可多次重復，如圖所示：

?1. 初探“self-attention層”內部機理

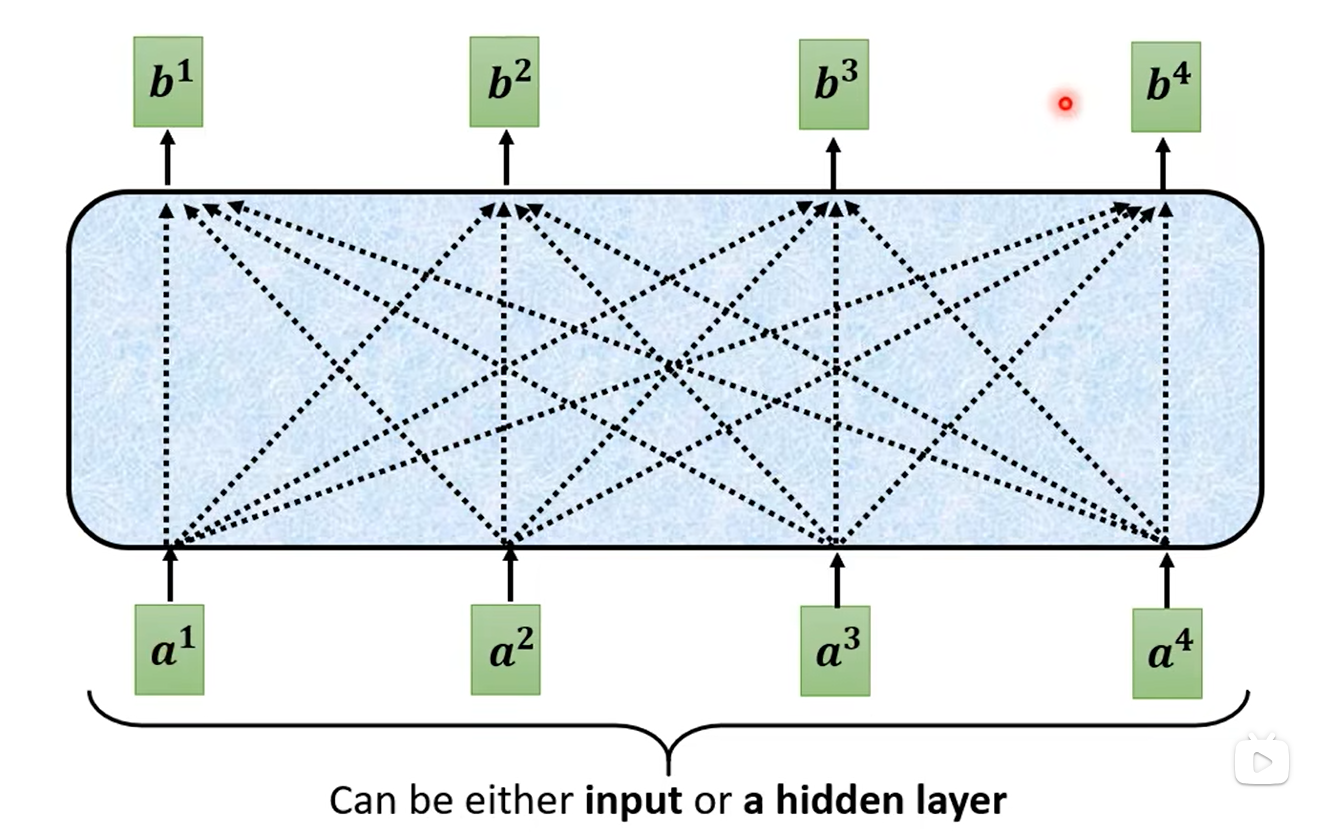
這里的a1-a4可以是輸入的向量，也可以是隱藏層的輸出，b1-b4都是觀察到全局的信息（即a1-a4）才得到的輸出，如下所示：

?那么這里的b1-b4又是如何產生的呢？b1考慮了a1和這個序列里面哪些是重要的，哪些是次要的。這種重要程度指標通過α表示，即向量之間都有一個相關程度：

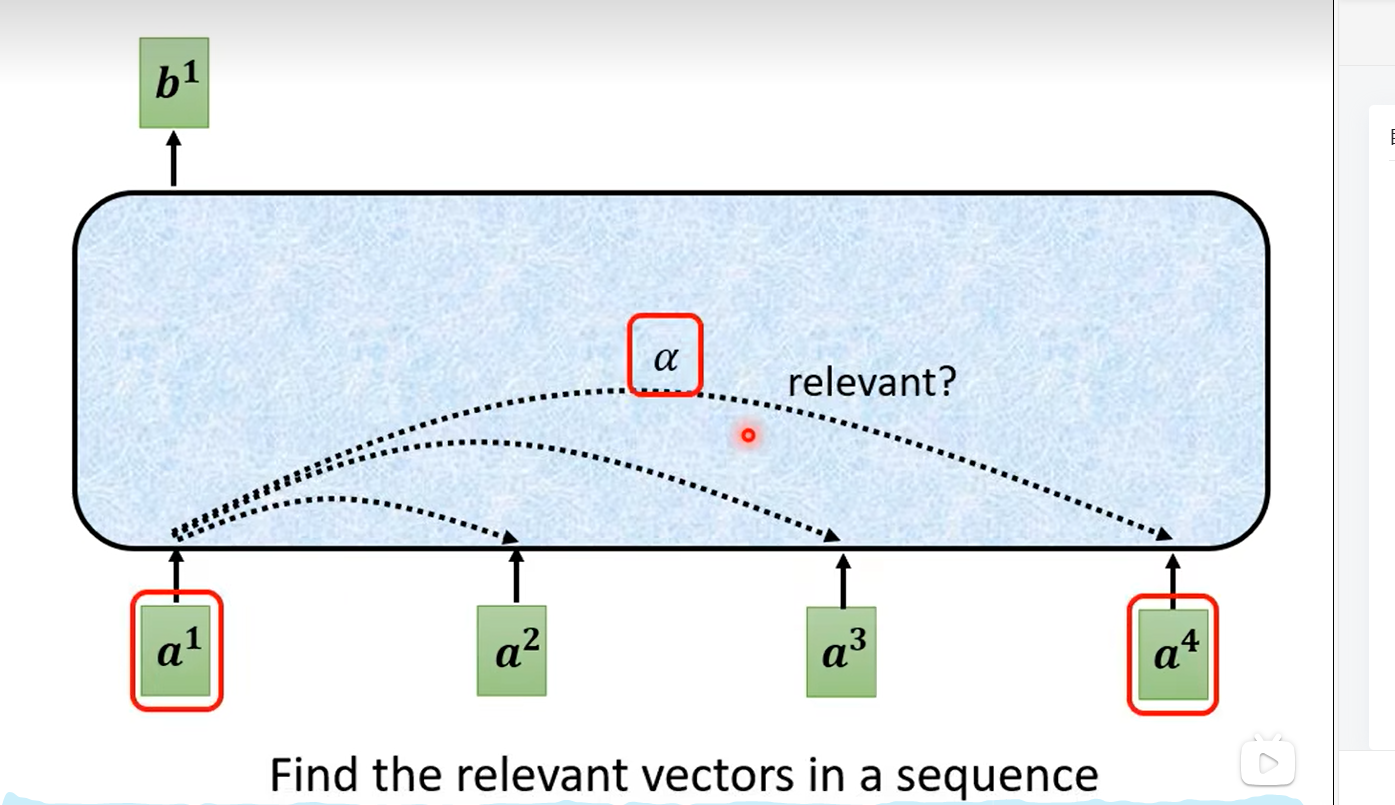
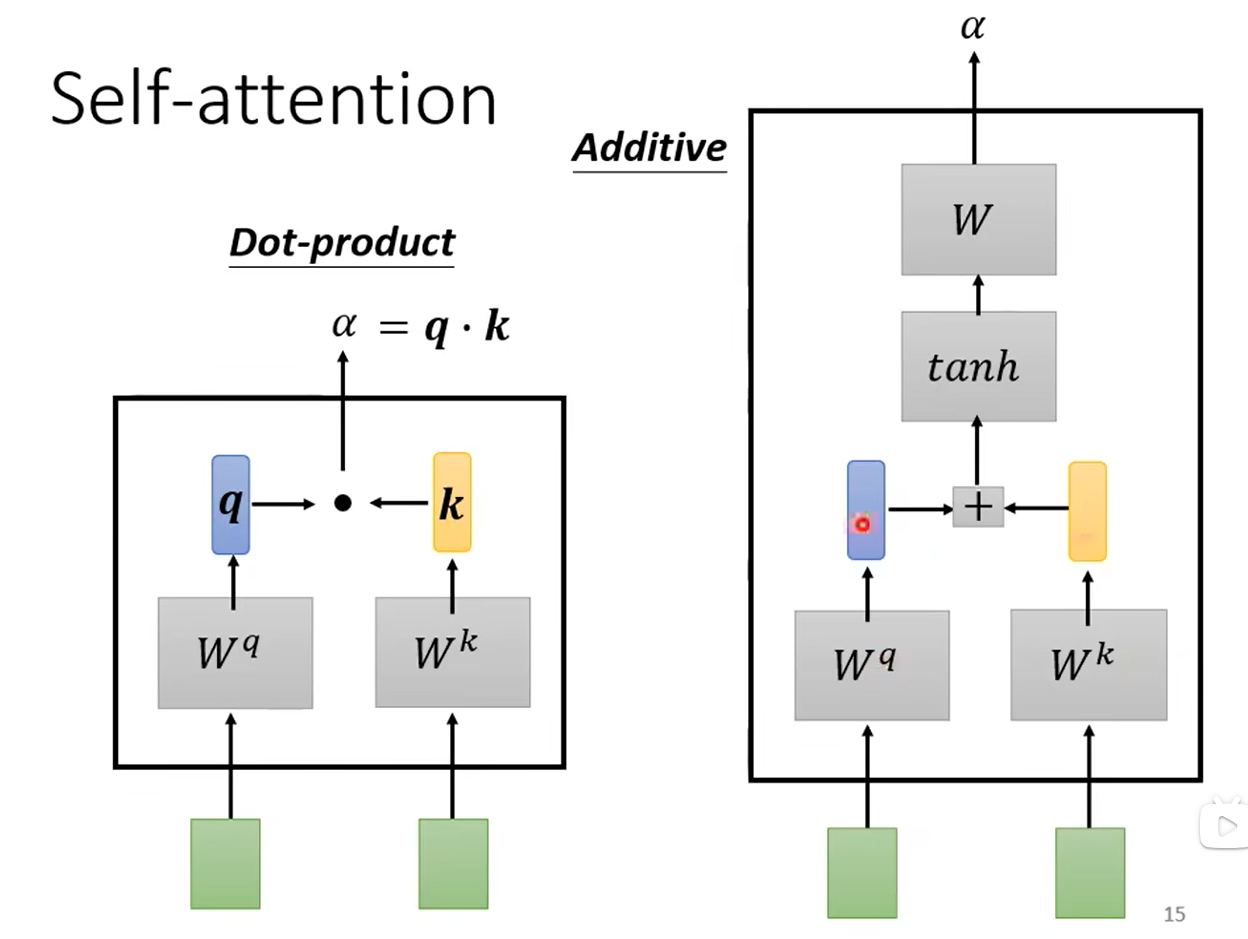
?接下來考慮α是如何計算的，下圖有兩種方法，論文用的是第一種（圖左側），因此著重講述。繼續使用上面的例子，綠色方塊代表兩個向量a1和a4，我們想計算它們的相關度，將其分別乘上矩陣Wq與Wk（這兩個矩陣是通過模型學習學到的）得到向量q與k，再將q與k做內積就得到α了。

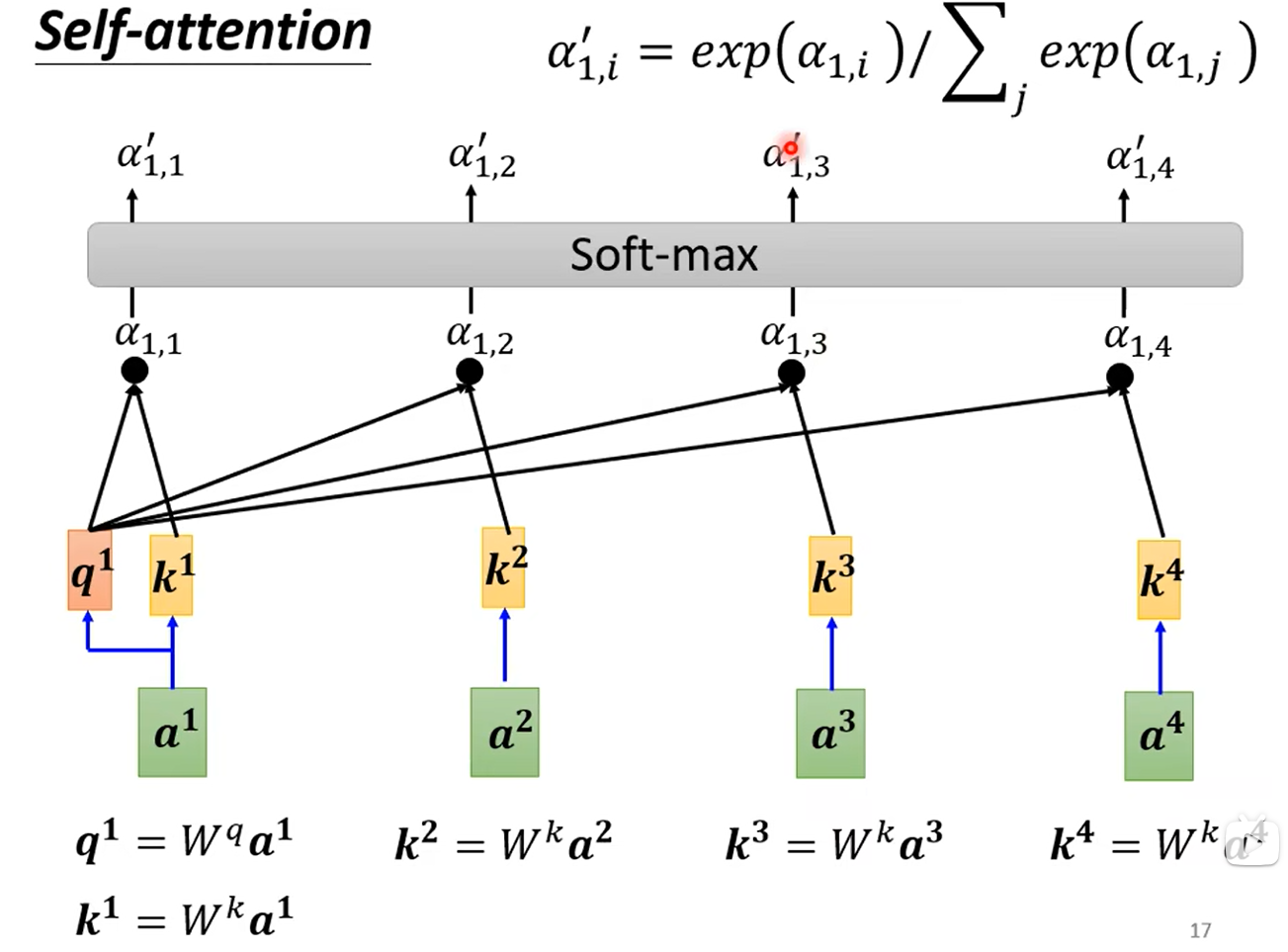
??這樣我們可以分別計算出a2、a3、a4對應的k2、k3、k4（Wk是這些向量所共享的），我們可以分別計算出a1與a2、a3、a4的相關度α1,2、α1,3、α1,4，當然α1,1是和自己的相關度，也可以算。如下所示：

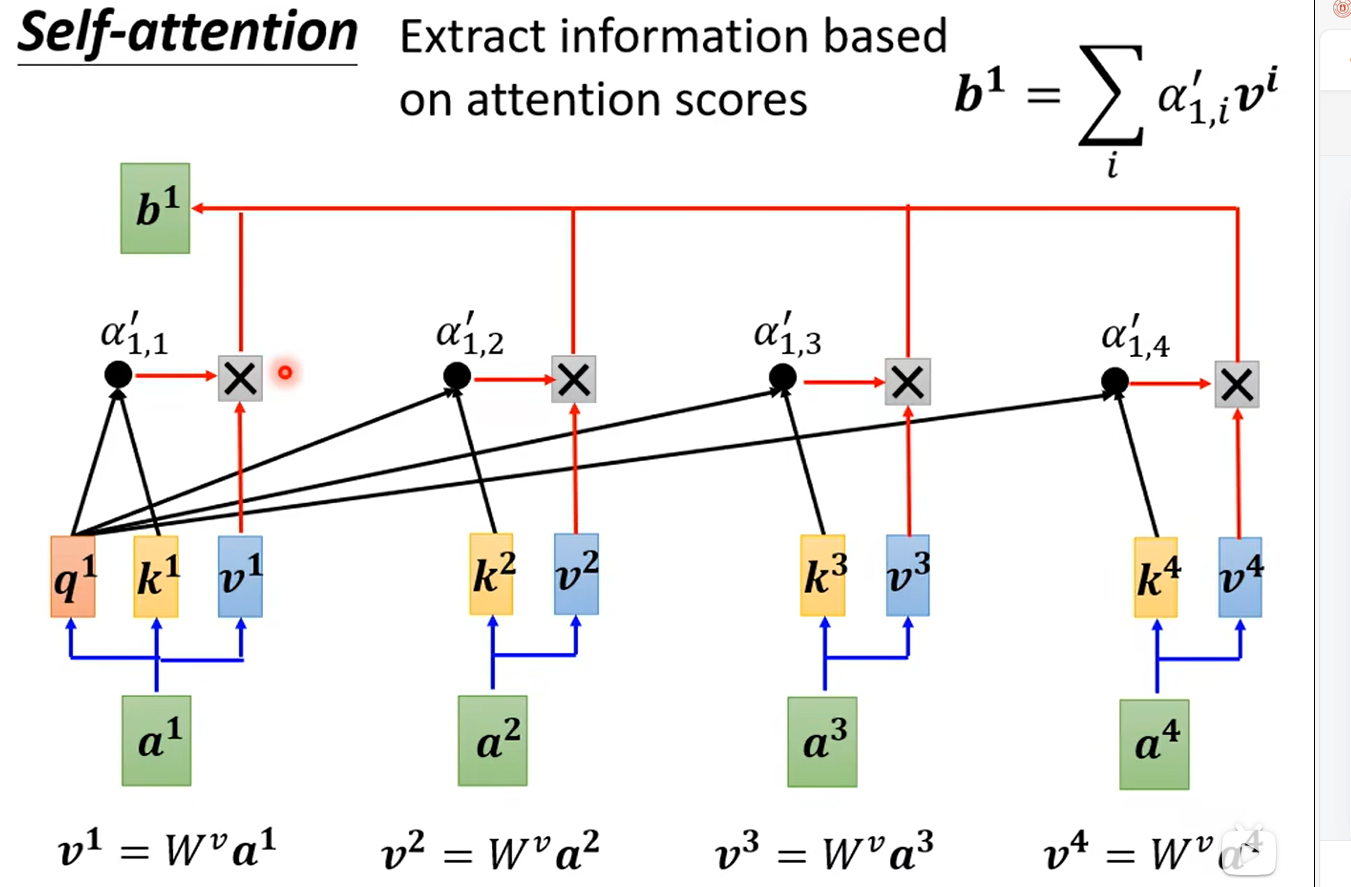
?有了α后，我們可以考慮b1-b4的計算了，怎么使用這些α抽取關注的特征呢？我們再引入一個矩陣Wv(同樣是學習得到的)，分別將a1-a4與Wv相乘得到v1-v4，將v1與α1,1相乘，v2與α1,2相乘...最后相加，即得到了b1。b2、b3、b4是同理的，下圖只畫出來了b1：

?2. 再探“self-attention層”內部機理

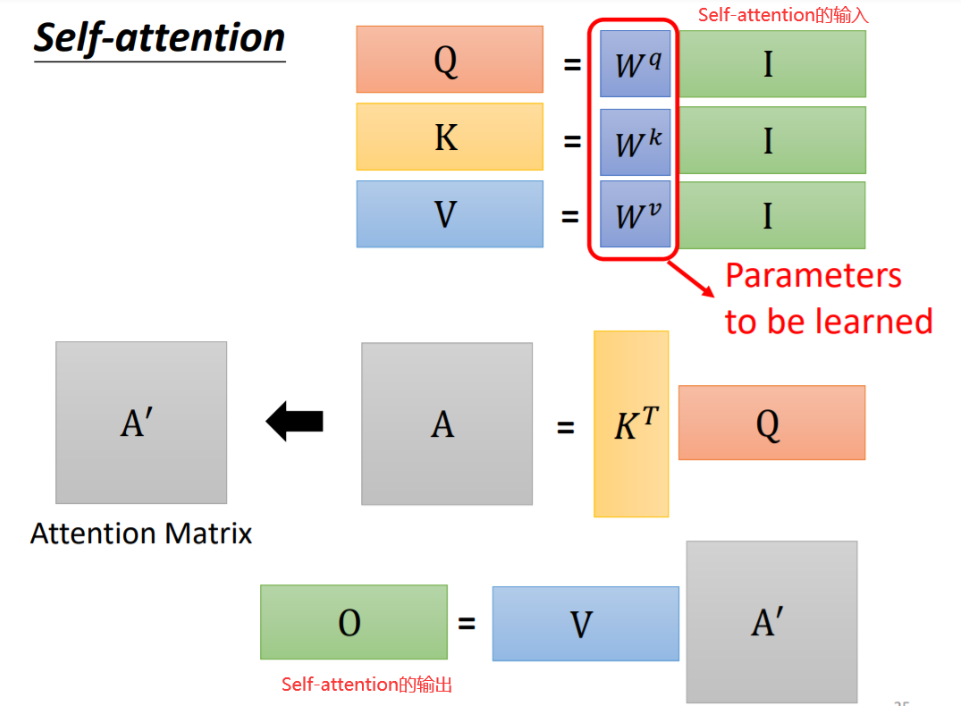
看起來可能復雜，但是實際上涉及的參數只有輸入的向量以及Wq、Wk、Wv三個矩陣。運算過程也都是矩陣乘法。我們從矩陣乘法的角度重新理解下，如下圖所示，我們將輸入向量a1-a4拼起來，分別乘Wq、Wk、Wv即得到了q1-a4、k1-k4、v1-v4：

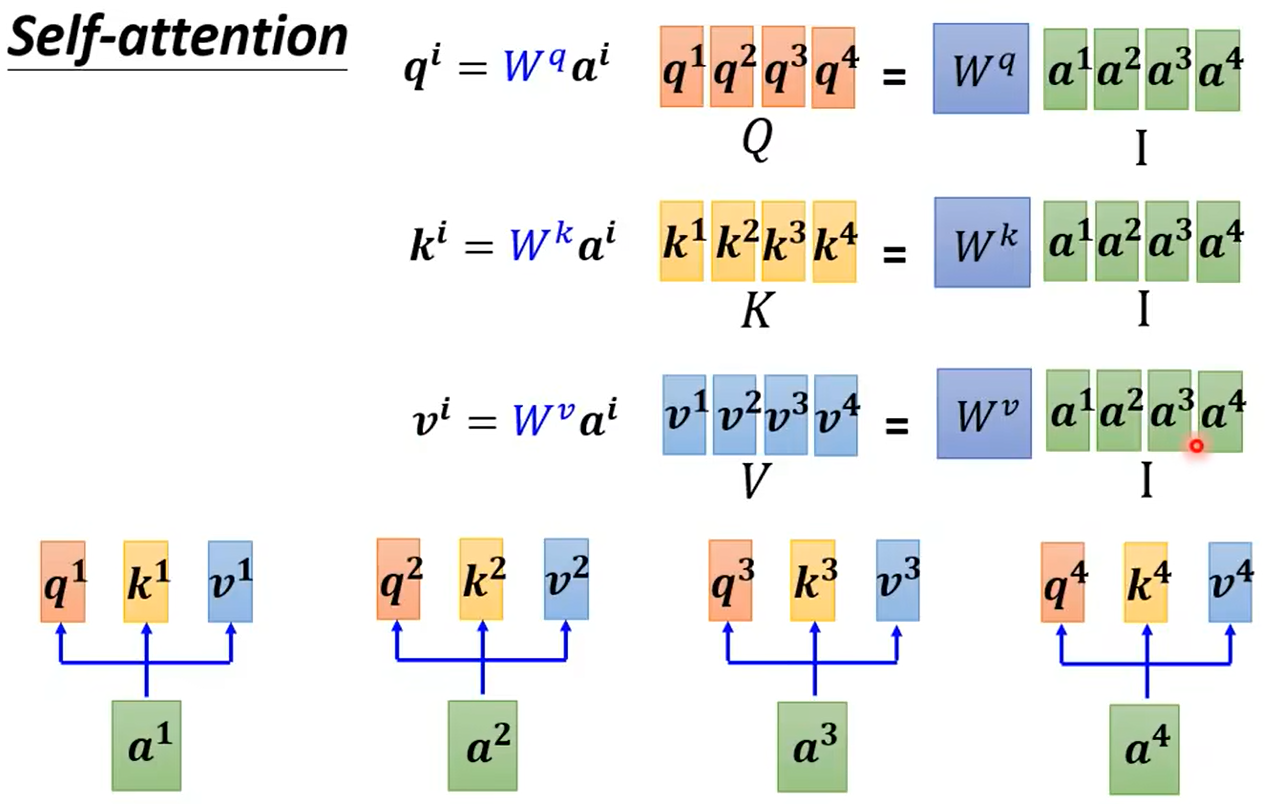
將k1-k4與q1-q4做內積即得到了每個向量與其他三個向量的相關度，如下圖所示，例如第一個向量與其他三個向量的相關度為α1,2、α1,3、α1,4,而α1,1代表和自己的相關度：

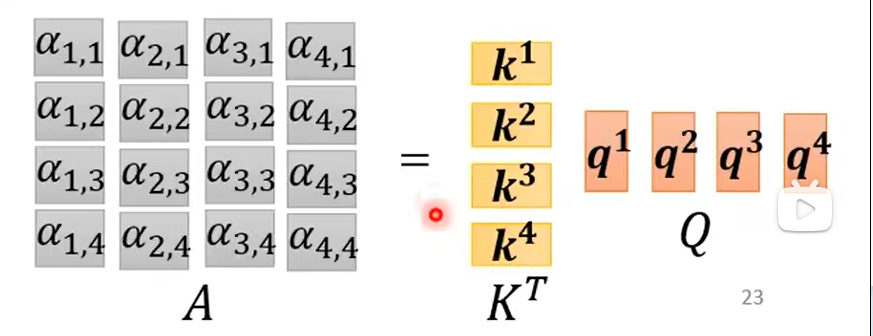
將α組成的矩陣記為A，經過softmax處理一下記為A':

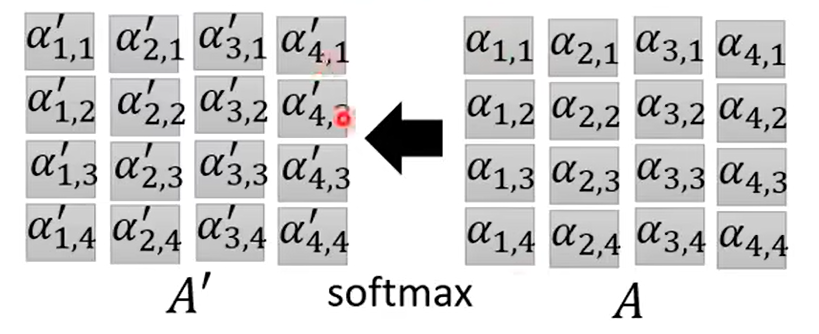
?v1-v4組成矩陣V，與A'相乘，根據矩陣乘法，V與A'的第一列相乘再相加的結果即為b1，同理可得b2-b4，b1-b4組成的矩陣就是最終的輸出了：

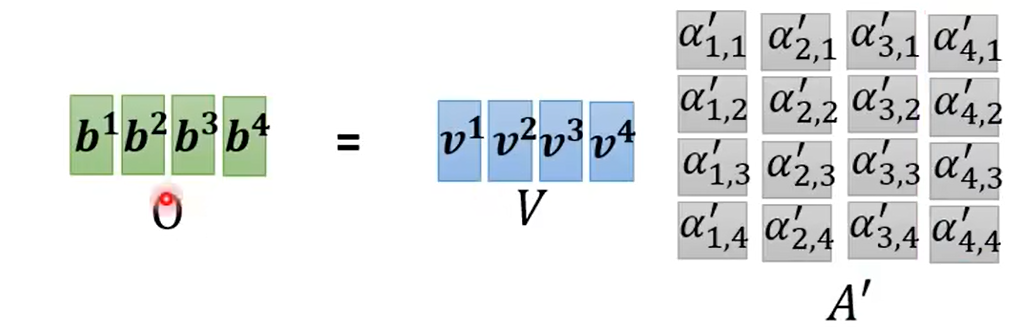
?3. 總結?

• 階段1：根據Q和K計算兩者的相似性或者相關性
• 階段2：對第一階段的原始分值進行歸一化處理
• 階段3：根據權重系數A'對V進行加權求和，得到最終的輸出