目錄
引言
學習目標
1.樹的概念及結構
1.1樹的定義
1.2樹的基本概念
1.3 樹的表示
(1)雙親表示法
(2)孩子表示法
(3)左孩子右兄弟表示法
1.4 樹在實際中的運用(表示文件系統的目錄樹結構)
結束語:
引言
之前我們學習了棧和隊列數據結構,接下來我們學習一種新的數據結構——樹
學習目標
- 為什么要學習為什么要學習非線性結構 ---- 樹(Tree)
- 數的定義和基本概念
- 樹的表示
- 樹的實際應用
- 樹的性質
為什么要學習非線性結構 ---- 樹(Tree)
線性結構的優缺點
在線性結構中,無論是順序存儲,還是鏈式存儲,線性表均有其優缺點:
- 順序表優點:
1:順序存儲可以在 O(1) 的時間內找到特定次序的元素(下標的隨機訪問)
2:CPU 高速緩存,命中率較高- 順序表缺點:?
1:順序存儲在,數據中間、頭部 的插入和刪除元素需要挪動大量元素,需要時間O(n)
2: ?順序存儲時,會出現空間不足,只能進行空間的擴容(異地擴容代價比較大)
- 鏈表優點:
1:在任意位置進行數據的插入和刪除的效率高,所需時間為O(1)
2: ?按需申請空間和釋放,不存在擴容- 鏈表的缺點:
1:在尋找特定次序的元素需要從鏈表頭部向后查找,需要時間O(n)
2:? CPU高速緩存,命中率低?
?其實鏈表和順序表是一個互補的數據結構
?
優化方案 ----- 樹(Tree)
樹形結構:很好的結合了順序表和鏈表的優點,可以在O(logn)的時間內完成查找、更新、插入、刪除等操作,在實際的應用中,很多算法可以借助于樹形結構高效的實現很多功能。
樹的講解流程
此時此刻大家肯定很想了解什么是樹,在本篇博客中,并不能把所有樹的結構在此篇文章中進行詳細的介紹,我會通過步步延申的方式去講解樹。
樹 ? 二叉樹? 搜索二叉樹 ? 平衡搜索二叉樹 (AVL樹和紅黑樹) ? M叉多叉平衡搜索樹 (B樹和B+樹)
1.樹的概念及結構
1.1樹的定義
- 有一個特殊的結點,稱為根結點,根結點沒有前驅結點
- 除根結點外,其余結點被分成M(M>0)個互不相交的集合T1、T2、……、Tm,其中每一個集合Ti(1<= i <= m)又是一棵結構與樹類似的子樹。每棵子樹的根結點有且只有一個前驅,可以有0個或多個后繼
- 因此,樹是遞歸定義的。

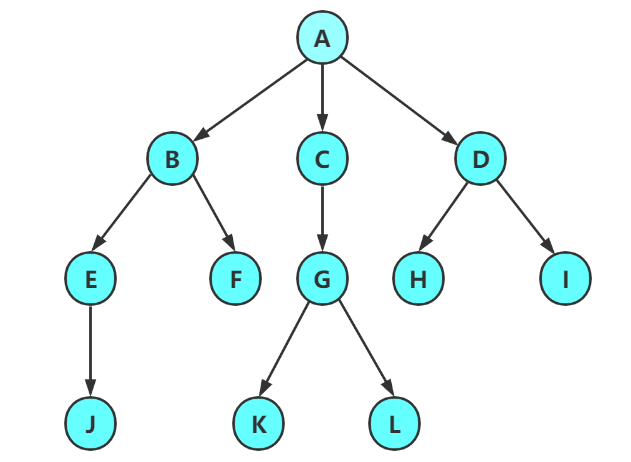
注意:樹形結構中,子樹之間不能有交集,否則就不是樹形結構。
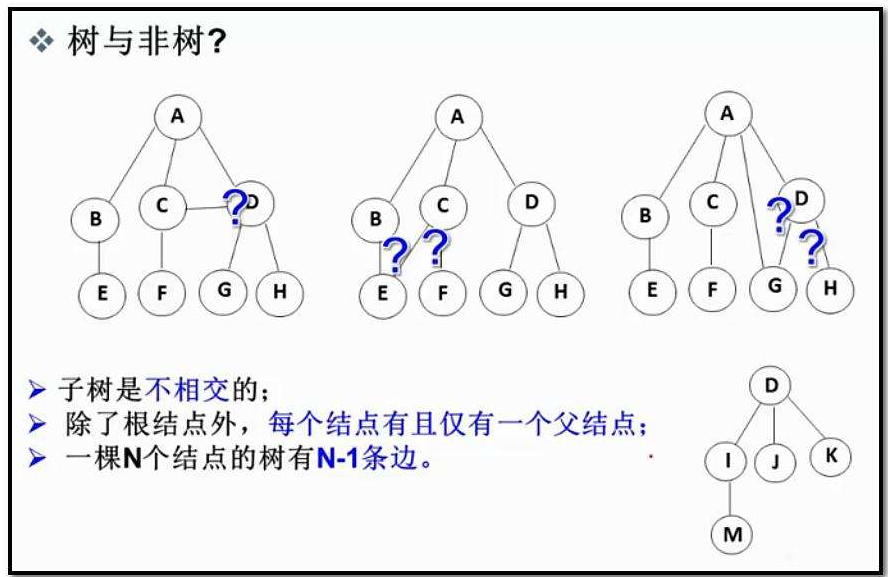
1.2樹的基本概念
我們根據這棵樹來介紹一下樹的基本概念
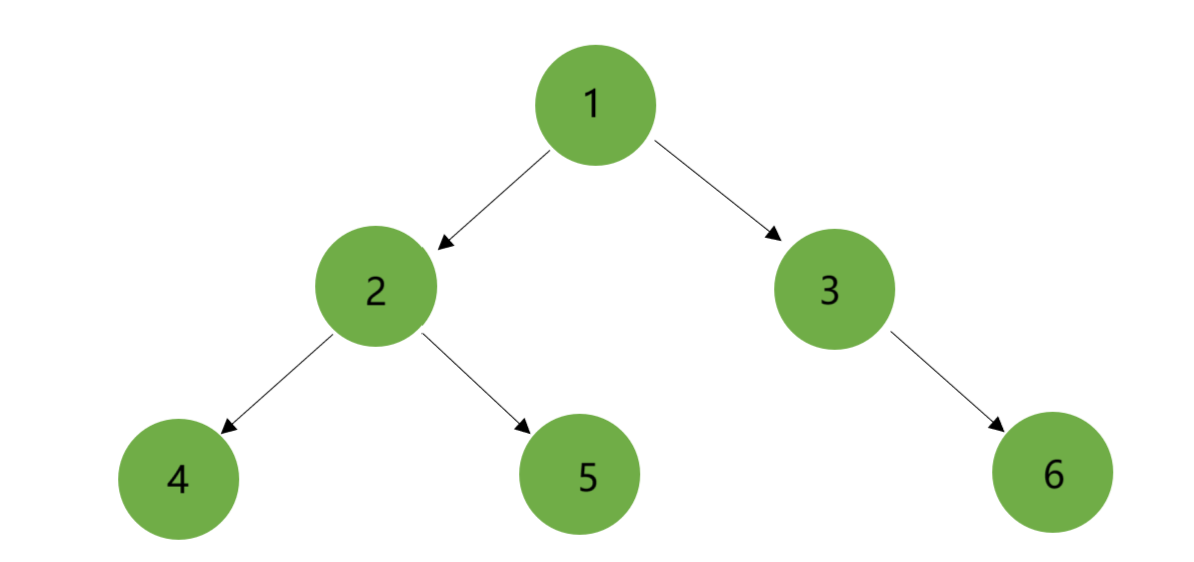
- 節點的度:一個節點含有的子樹的個數稱為該節點的度,比如說節點1的度為2
- 葉節點或終端節點:度為0的節點,比如說4,5,6節點
- 非終端節點或分支節點:度不為0的節點,比如說2,3節點
- 雙親結點或父節點:若一個節點含有子節點,則這個節點稱為其子節點的父節點。比如? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 說2是4,5的父節點
- 孩子節點或子節點:一個節點含有的子樹的根節點稱為該節點的子節點,比如說4,5是? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 2的子節點
- 兄弟節點:具有相同父節點的節點互稱為兄弟節點,比如說4,5就是兄弟節點
- 樹的度:一棵樹中,最大的節點的度稱為樹的度,比如說上面這棵樹的度為2
- 節點的層次:從根開始定義起,根為第1層,根的子節點為第2層,以此類推
- 樹的高度或深度:樹中節點的最大層次,比如說上面這棵樹的高度為3
- 堂兄弟節點:雙親在同一層的節點互為堂兄弟,比如說5,6節點
- 節點的祖先:從根到該節點所經分支上的所有節點,比如說1就是所有節點的祖先
- 子孫:以某節點為根的子樹中任一節點都稱為該節點的子孫,比如說所有節點都是1的? ? ? ? ? ? ?子孫
- 森林:由m(m>0)棵互不相交的樹的集合稱為森林
1.3 樹的表示
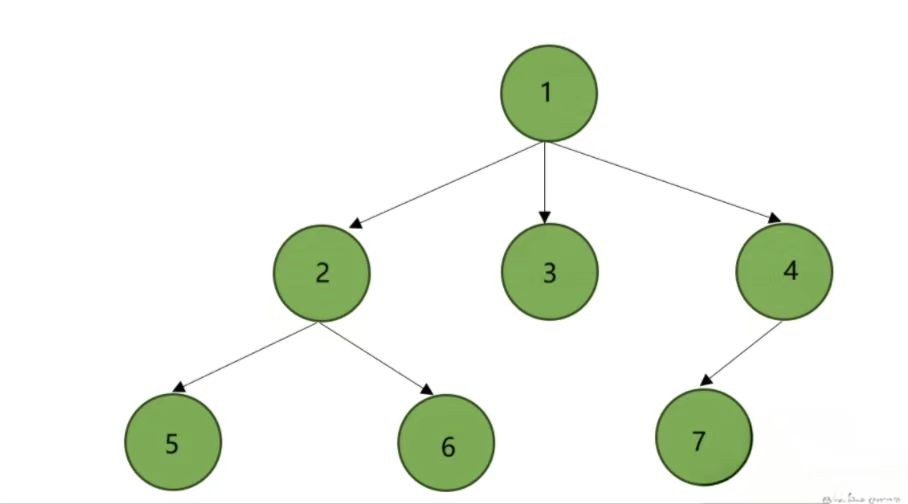
我們有三種方法表示上面這棵樹:
(1)雙親表示法
雙親表示法是用順序表,也就是數組對樹進行表示的。即用順序表存儲各個節點的數據,并且同時存儲其雙親節點的下標。
注意:根節點沒有雙親節點,所以特別記為-1。
聲明如下:

如下圖所示:
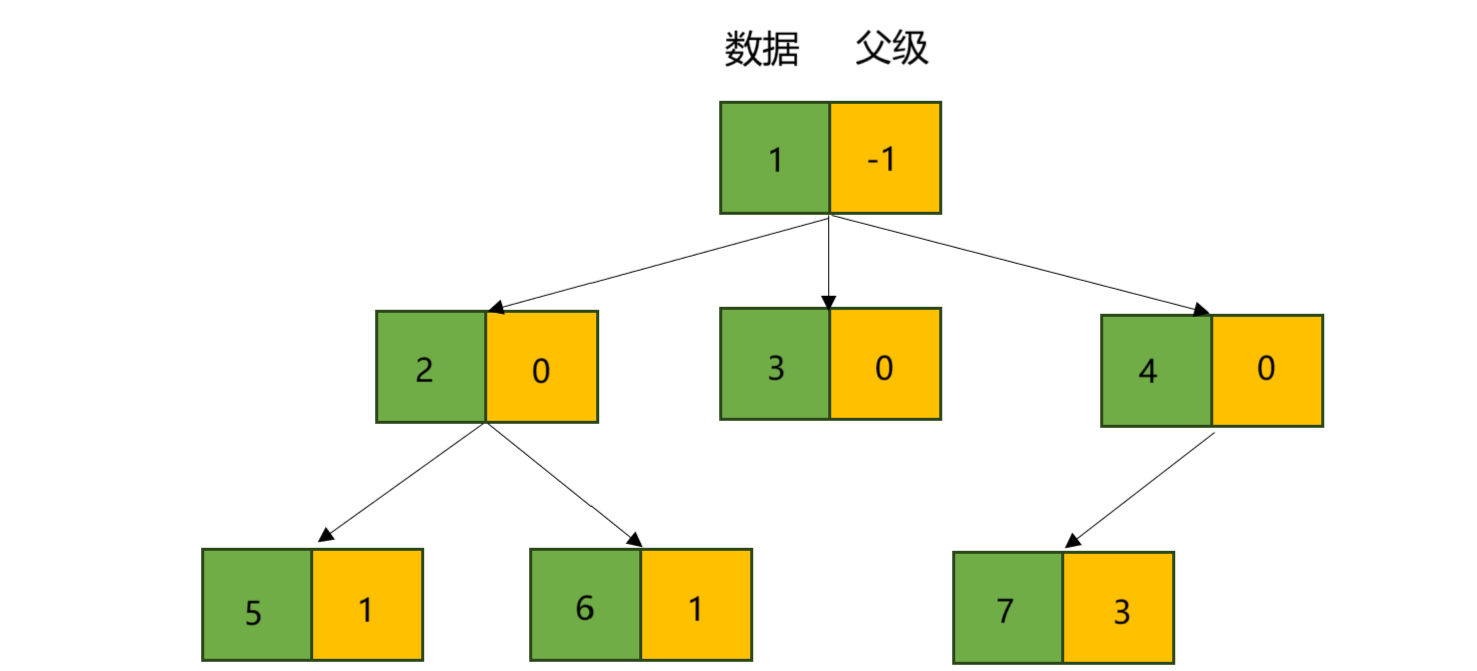
存儲方式如下:
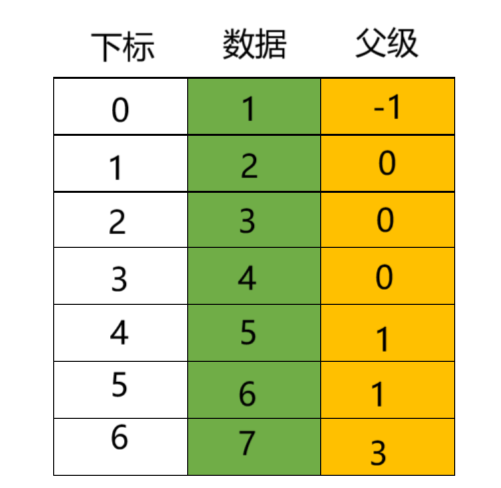
說明:
- 因為根節點沒有父節點,將其父節點數組下標設置為-1,根節點存儲在順序表的第1個位置。
- 數據元素2、3、4的父節點為0,父節點數組下標為0,分別存儲在順序表的2、3、4個位置。
- 數據元素5、6的父節點為1,父節點數組下標為1,分別存儲在順序表的第5、6個位置。
- 數據元素7的父節點為3,父節點數組下標為3,存儲在順序表的第7個位置。
#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 10
typedef int DataType;
typedef struct TreeNode
{DataType data;int parent;
}Node;typedef struct ParentTree
{// 數據結構的樹節點Node Tnode[MAXSIZE];int n; //當前節點個數
}Ptree;// 初始化樹
void TreeInit(Ptree* ptree, int x, int parentIndex)
{if (ptree->n >= MAXSIZE) {printf("Tree is full!\n");return;}ptree->Tnode[ptree->n].data = x;ptree->Tnode[ptree->n].parent = parentIndex;ptree->n++; // 增加節點計數
}雙親表示法的特點:
- 優點:快速查找一個結點的父結點(直接通過
parent字段獲取),結構簡單,空間開銷小(僅需存儲值和一個索引)。 - 缺點:查找子結點時效率低(需遍歷整個數組,判斷哪些結點的
parent等于當前結點的索引),不適合頻繁查找子結點的場景。
(2)孩子表示法
樹的孩子表示法就是采用順序表與鏈表結合的形式,用順序表存儲樹的值與鏈表的頭節點,而鏈表的頭節點存儲其孩子節點在順序表中的下標,若沒有則記為空(NULL)。
相當于對樹進行這樣的處理:
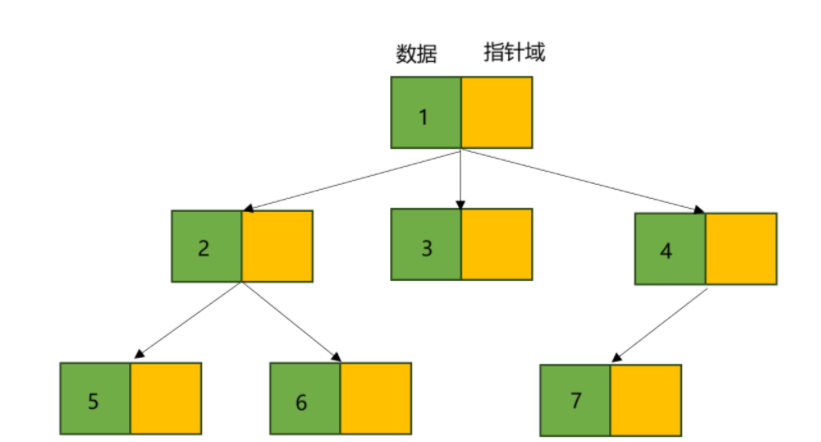
存儲方式如下:
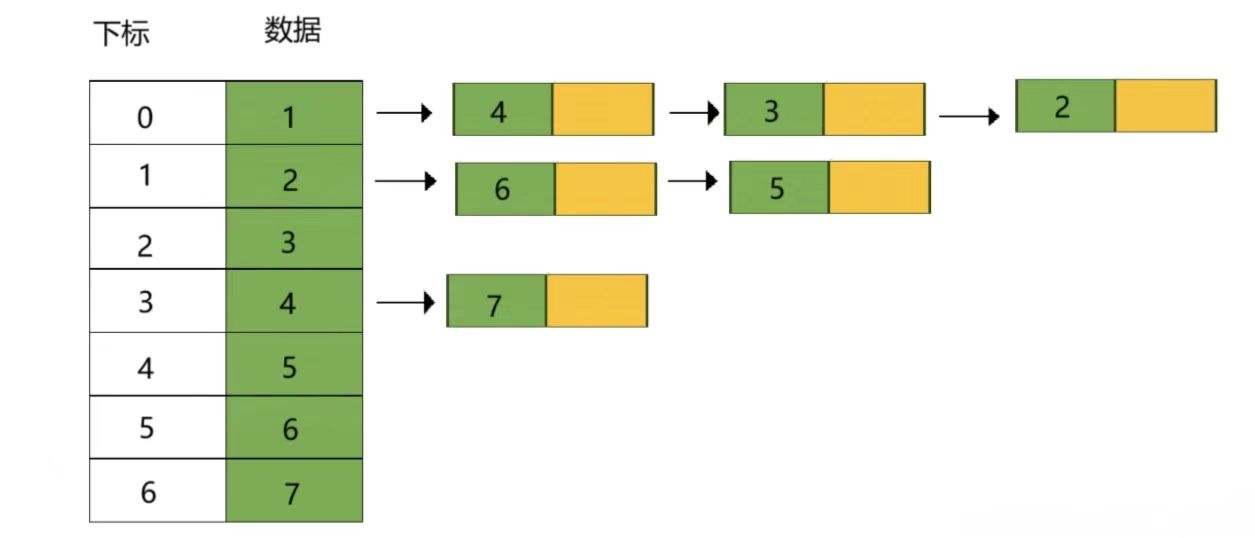
說明:
添加一個數據(插入一個結點)
- 既要在數組中依次添加新的數據。
- 也要在其父節點后面用頭插法插入。
優缺點:
- 優點:簡單且易于理解,適用于需要頻繁查找孩子節點的應用場景。
- 缺點:不容易直接獲取節點的父節點。
代碼如下:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>#define MAXSIZE 10
typedef int DataType;
typedef struct ListNode
{int index;struct ListNode* next;
}ListNode;typedef struct TreeNode
{DataType data;ListNode* child;
}TNode;typedef struct Tree
{TNode nodes[MAXSIZE];int n;
}Tree;// 創建一個新的ListNode
ListNode* createListNode(int index)
{ListNode* newNode = (ListNode*)malloc(sizeof(ListNode));if (newNode == NULL){perror("malloc fail:");exit(0);}newNode->index = index;newNode->next = NULL;return newNode;
}// 初始化樹
void TreeInit(Tree* t, DataType x)
{if (t->n >= MAXSIZE) {printf("Tree is full!\n");return;}t->nodes[t->n].data = x;t->nodes[t->n].child = NULL; t->n++;
}// 向節點的子鏈表中添加一個新節點
void InsertChild(Tree* t, int parentIndex, int childIndex)
{if (parentIndex >= t->n || childIndex >= t->n) {printf("error\n");return;}ListNode* newNode = createListNode(childIndex);if (newNode == NULL){perror("malloc fail:");return; // 內存分配失敗 }newNode->next = t->nodes[parentIndex].child;t->nodes[parentIndex].child = newNode;
}(3)左孩子右兄弟表示法
最常用表示樹的的方法就是左孩子右兄弟表示法,即定義兩個指針,讓左指針指向子節點,右指針指向兄弟節點。如果沒有節點,則都指向空(NULL)。
如圖所示:
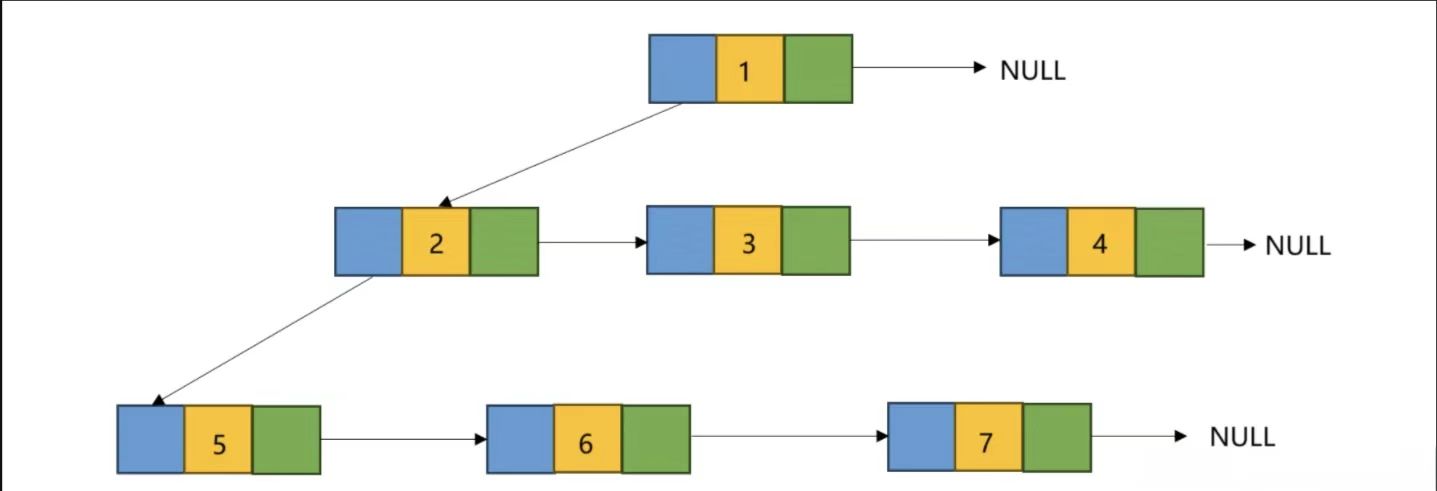
- 基本原理:在這種表示法中,每個節點包含一個數據域和兩個指針域。其中一個指針指向該節點的第一個孩子節點(左孩子),另一個指針指向該節點的下一個兄弟節點(右兄弟)。通過這種方式,可將任意一棵多叉樹轉化為一棵二叉樹來表示。
節點定義:在 C++ 中,可按如下方式定義節點結構:

代碼如下:
#include <stdio.h>
#include <stdlib.h>
typedef int DataType;typedef struct TreeNode
{DataType data;struct TreeNode* leftChild; // 指向左孩子 struct TreeNode* rightBro; // 指向右兄弟
} TNode;// 創建一個新的樹節點
TNode* createTreeNode(DataType x)
{TNode* newNode = (TNode*)malloc(sizeof(TNode));if (newNode == NULL){perror("malloc fail:");exit(0);}newNode->data = x;newNode->leftChild = NULL;newNode->rightBro = NULL;return newNode;
}void InsertChild(TNode* t, DataType x, int isLeftChild)
{if (t == NULL) {printf("Cannot insert into NULL node\n");return;}TNode* newNode = createTreeNode(x);if (newNode == NULL) {return;}// 如果isLeftChild為1,表示新節點應該作為左孩子插入 if (isLeftChild) {// 如果當前節點還沒有右兄弟,則直接將新節點設置為右兄弟if (t->leftChild == NULL) {t->leftChild = newNode;}// 如果當前節點已經有左孩子,則遍歷左孩子的右兄弟鏈表// 找到最后一個右兄弟,并將新節點插入為它的下一個右兄弟else {TNode* tmp = t->leftChild;while (tmp->rightBro != NULL) {tmp = tmp->rightBro;}tmp->rightBro = newNode;}}// 如果isLeftChild為0,表示新節點應該作為右兄弟插入else{// 如果當前節點還沒有右兄弟,則直接將新節點設置為右兄弟if (t->rightBro == NULL) {t->rightBro = newNode;}// 如果當前節點已經有右兄弟,則遍歷右兄弟鏈表// 找到最后一個右兄弟,并將新節點插入為它的下一個右兄弟else {TNode* tmp = t->rightBro;while (tmp->rightBro != NULL) {tmp = tmp->rightBro;}tmp->rightBro = newNode;}}
}1.4 樹在實際中的運用(表示文件系統的目錄樹結構)
在linux環境下目錄結構就是有一顆樹構成,而在Windows環境下,目錄許多內容并不交叉,所以是由森林構成。
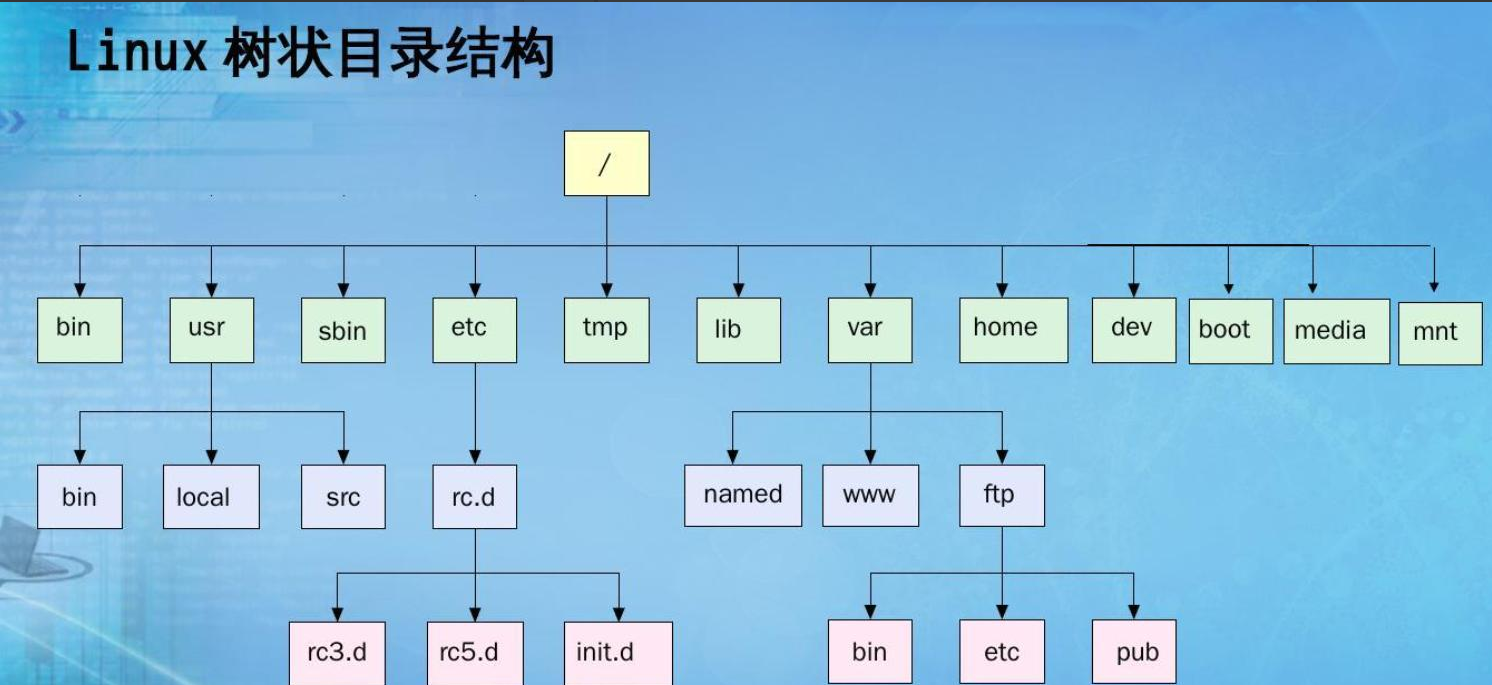
?樹的性質(重點)
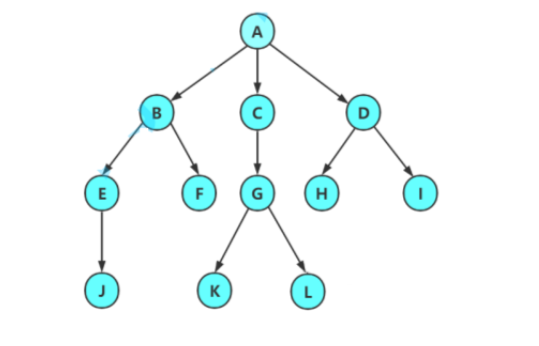
?性質1:樹中的節點數等于所有節點度數加 1
????????從上圖可知,有 12 個節點 ?,A的度為:3, B的度為2, C 的度為1, D的度為2, E的度為1, F的度為0, G的度為2, H的度為0 , I的度為0,J的度為0,K的度0,L的度為0。
????????由性質 1 可知 樹的節點個數 = 每個節點的度數 + 1?所以上圖 樹的節點數 = (3+2+1+2+1+0+2+0+0+0+0+0)+1 = 12
?性質2:度為 m 的樹中第 i 層至多有 m^i-1 個節點(i>=1)
性質3:高度為 h 的 m 叉樹至多有? m^h-1/m-1 個節點
性質4:具有n個結點的m叉樹的最小高度為?logm(n*(m-1)+1)?
結束語:
下一節我們將繼續深入學習樹的知識
感謝你的三連支持!!!

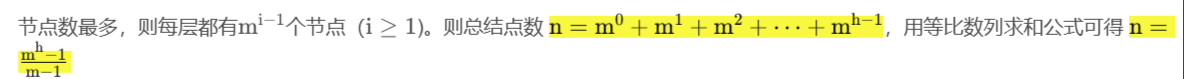
















)



