3個不同的API可供評估模型預測質量:
-
評估器評分方法:評估器有一個score方法,它給計劃解決的問題提供一個初始評估標準。這部分內容不在這里討論,但會出現在每一個評估器的文件中。
-
評分參數:使用交叉驗證(cross-validation)的模型評估方法(例如:model_selection.cross_val_score和model_selection.GridSearchCV基于一個內部評分策略。這部分內容將會在評分參數:定義模型評估規則部分詳細介紹。
-
指標函數:metrics模塊執行的功能是評估特定目的的誤差。這些指標在分類指標, 多標簽排序指標, 回歸指標和聚類指標部分會詳細介紹。
最后,Dummy評估器(Dummy評估器)可用于獲取隨機預測的這些指標基準值。
還可參見:對于“成對”指標,樣本之間而不是評估器或者預測值之間,詳見成對度量、親和力和核函數部分。
一、評分參數:定義模型評估準則
1.1 常見場景:預定義值
在最常見的例子中,可以給scoring參數指定評分對象;下面的表格列出所有可能取值。所有記分對象遵從的慣例是:高返回值好于低返回值。因此,如metrics.mean_squared_error,衡量模型與數據間差距的指標可用neg_mean_squared_error,它返回一個負值。
| 評分 | 函數 | 評論 |
|---|---|---|
| 分類 | ||
| “accuracy”(準確率) | metrics.accuracy_score | |
| “balanced_accuracy”(平衡準確率) | metrics.balanced_accuracy_score | |
| “average_precision”(平均精確率) | metrics.average_precision_score | |
| “neg_brier_score”(負布里爾評分) | metrics.brier_score_loss | |
| “f1” | metrics.f1_score | 二分類 |
| “f1_micro” | metrics.f1_score | 微平均 |
| “f1_macro” | metrics.f1_score | 宏平均 |
| “f1_weighted” | metrics.f1_score | 加權平均 |
| “f1_samples” | metrics.f1_score | 多標簽樣本 |
| “neg_log_loss” | metrics.log_loss | 要求predict_proba支持 |
| "precision"等 | metrics.precision_score | 后綴適用于“f1” |
示例:
>>> from sklearn import svm, datasets
>>> from sklearn.model_selection import cross_val_score
>>> X,y = datasets.load_iris(return_X_y=True)
>>> clf=svm.SVC(random_state=0)
>>>cross_val_score(c1f,x,y,cv=5,scoring='reca11_macro')
array([0.96..., 0.96..., 0.96..., 0.93..., 1. ]
>>> model = svm.SVC()
>>>cross_val score(model,X,y,cv=5,scoring='wrong_choice')
Traceback (most recent call last):
ValueError: 'wrong_choice' is not a valid scoring value. Use sorted (sklearn.metrics.SCORERS.keys()) to get va
注意:ValueError列出的異常值對應于以下各節中說明的測量預測準確性函數。這些函數中的評分對象以字典形式存儲在 sklearn.metrics.SCORES中。
1.2 根據metric函數定義評分策略
sklearn.metrics模塊公開一組簡單函數,該函數可應用于測量給定真實值和預測值的預測誤差:
- 以_score為結尾的函數,返回一個最大值,該值越大越好。
- 以_error或_loss為結尾的函數,返回一個最小值,該值越小越好。當使用make_scorer把它轉變為評分對象時,設置greater_is_better參數為False(初始值是True;詳見下面的函數描述)。
各類機器學習任務的可用指標會在下文詳細介紹。
許多指標沒有給定名稱就作為scoring的參數值,有時是因為它們需要額外的參數,例如fbeta_score。使用make_scorer是生成可調用對象進行評分的最簡單方法,該函數將指標轉換為可用于模型評估的可調用對象。
一個典型的例子是從庫中包含一個非默認參數值中,包裝現有指標函數,例如fbeta_score函數用來定義beta參數:
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
... scoring=ftwo_scorer, cv=5)
第二個例子是在簡單python函數中使用make_scorer,以構建完全自定義評分對象,它可以接受幾個參數:
-
可以使用的python函數(下例中使用my_custom_loss_func)
-
是否python函數返回一個分數(初始值為greater_is_better=True)或者一個損失(分數)(greater_is_better=False)。如果一個損失函數,python函數的返回值是負值的評分對象,符合交叉驗證的傳統,評分越高,模型越好。
-
僅對于分類的指標:是否python函數要求提供連續決定確定性(needs_threshold=True)。初始值是False。
-
任何其它參數,如f1_score中的beta或labels。
如下示例展示構建傳統評分器,使用greater_is_better參數:
>>> import numpy as np
>>> def my_custom_loss_func(y_true, y_pred):
... diff = np.abs(y_true - y_pred).max()
... return np.log1p(diff)
...
>>> # score will negate the return value of my_custom_loss_func,
>>> # which will be np.log(2), 0.693, given the values for X
>>> # and y defined below.
>>> score = make_scorer(my_custom_loss_func, greater_is_better=False)
>>> X = [[1], [1]]
>>> y = [0, 1]
>>> from sklearn.dummy import DummyClassifier
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf = clf.fit(X, y)
>>> my_custom_loss_func(clf.predict(X), y)
0.69...
>>> score(clf, X, y)
-0.69...
1.3 執行自定義評分對象
無需使用make_scorer“制造廠”,就可以通過從頭構建自定義評分對象,生成更加靈活的模型評分器。對于一個可調用的評分器,需要滿足如下兩個規定協議:
- 可以調用參數(estimator, X, y),estimator是需要被評估的模型,X是驗證數據,y是X標簽(應用于有監督的案例中)的真實值或者None(應用于非監督的案例中)。
- 它返回一個浮點型數值,該數值量化estimator對X關于y的預測質量。再強調一遍,越高的得分模型越好,所以如果得分是損失函數的返回值,那么該值應為負。
注意:當n_jobs>1時,函數中對傳統評分器的使用
雖然在調用函數的旁邊定義自定義評分函數應使用默認joblib backend(loky),但從另一個模塊中導入時將會是更健壯的方法,并且獨立于joblib backend(loky)。
例如,下例中將n_jobs設置為大于1,custom_scoring_function保存在user_created模塊(custom_scorer_module.py)中并導入:
>>> from custom_scorer_module import custom_scoring_function
>>> cross_val_score(model,
... X_train,
... y_train,
... scoring=make_scorer(custom_scoring_function, greater_is_better=False),
... cv=5,
... n_jobs=-1)
1.4 使用多指標評估
Scikit-learn也允許在GridSearchCV,RandomizedSearchCV和cross_validate中評估多指標。
有兩種方式可以指定scoring參數的多評分指標:
- 可迭代字符串指標:
>>> scoring = ['accuracy', 'precision']
以字典形式將評分器名稱映射給評分函數:
深色版本
>>> from sklearn.metrics import accuracy_score
>>> from sklearn.metrics import make_scorer
>>> scoring = {'accuracy': make_scorer(accuracy_score),
... 'prec': 'precision'}
需要注意的是:字典的值或者是評分器函數,或者是預定義指標字符串的一個。
目前,只有返回單值的評分函數才能使用字典傳遞。評分函數返回多個值是不被允許的,并且要求封裝從而返回單個指標值。
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import confusion_matrix
>>> # A sample toy binary classification dataset
>>> X, y = datasets.make_classification(n_classes=2, random_state=0)
>>> svm = LinearSVC(random_state=0)
>>> def tn(y_true, y_pred): return confusion_matrix(y_true, y_pred)[0, 0]
>>> def fp(y_true, y_pred): return confusion_matrix(y_true, y_pred)[0, 1]
>>> def fn(y_true, y_pred): return confusion_matrix(y_true, y_pred)[1, 0]
>>> def tp(y_true, y_pred): return confusion_matrix(y_true, y_pred)[1, 1]
>>> scoring = {'tp': make_scorer(tp), 'tn': make_scorer(tn),
... 'fp': make_scorer(fp), 'fn': make_scorer(fn)}
>>> cv_results = cross_validate(svm.fit(X, y), X, y, cv=5, scoring=scoring)
>>> # Getting the test set true positive scores
>>> print(cv_results['test_tp'])
[10 9 8 7 8]
>>> # Getting the test set false negative scores
>>> print(cv_results['test_fn'])
[0 1 2 3 2]
二、分類指標
sklearn.metrics模塊執行各種損失函數,評分,及調用函數測量分類模型的表現。一些指標可能要求正類別的可能性(probability)估計,置信度值,或者二分類決策值。大多數執行允許計算每一個樣本對評分的權重貢獻,通過sample_weight參數實現。
其中一些只適用于二分類的案例中:
| 參數 | 說明 |
|---|---|
precision_recall_curve(y_true, probs_pred, *) | 根據不同的可能性閾值計算精確率-召回率 |
roc_curve(y_true, y_score, *[pos_label, ...]) | 計算Receiver operating characteristic(ROC) |
其它也可用于多分類的參數例子:
| 參數 | 說明 |
|---|---|
balanced_accuracy_score(y_true, y_pred, *) | 計算balanced準確率 |
cohen_kappa_score(y1, y2, *[labels, ...]) | Cohen’s kappa: 衡量注一致程度的統計 |
confusion_matrix(y_true, y_pred, *[...]) | 計算混淆矩陣來評估分類模型的準確率 |
hinge_loss(y_true, pred_decision, *[...]) | 平均hinge損失(非正規 non-regularized) |
matthews_corrcoef(y_true, y_pred, *[...]) | 計算曼哈頓相關系數(MCC) |
roc_auc_score(y_true, y_score, *[...]) | 從預測分數中,計算ROC曲線的面積(ROC AUC) |
一些也可以用于多分類例子中的參數:
| 參數 | 說明 |
|---|---|
accuracy_score(y_true, y_pred, *[...]) | 分類模型的準確率得分 |
classification_report(y_true, y_pred, *[...]) | 主要分類模型指標的文本報告 |
f1_score(y_true, y_pred, *[labels, ...]) | 計算F1評分,也被稱為balanced F-score或者F-measure |
fbeta_score(y_true, y_pred, *, beta[, ...]) | 計算F-beta評分 |
hamming_loss(y_true, y_pred, *[sample_weight]) | 計算平均Hamming損失 |
jaccard_score(y_true, y_pred, *[labels, ...]) | Jaccard相似性系數得分 |
log_loss(y_true, y_pred, *[eps, ...]) | 對數損失,aka logistic損失或者交叉熵損失 |
multilabel_confusion_matrix(y_true, y_pred, *) | 為每一個類或樣本計算混淆矩陣 |
precision_recall_fscore_support(y_true, ...) | 計算精確率,召回率,F-measure并且支持每一個類 |
precision_score(y_true, y_pred, *[...]) | 計算精確率 |
recall_score(y_true, y_pred, *[labels, ...]) | 計算召回率 |
roc_auc_score(y_true, y_score, *[...]) | 從預測分數中計算ROC曲線的面積 |
zero_one_loss(y_true, y_pred, *[...]) | 0-1分類損失 |
可以處理二分類和多標簽(不是多分類)的問題:
| 參數 | 說明 |
|---|---|
average_precision_score(y_true, y_score, *) | 從預測評分中計算平均精確率(AP) |
在隨后的各子部分中,將會描述每一個上述函數,使用常用的API和指數定義。
2.1 從二分類到多分類和多標簽
一些指標本質上是定義給二分類模型的(例如:f1_score)。在這些例子中,模型的默認值是只有正標簽會被評估,假設正樣本類的標簽為1是初始值(盡管標簽可以通過pos_label參數進行修改)。
由二分類指標延伸到多類或者多標簽問題,數據被當作是二分類問題的集合,每個類都有一個。有一系列的方法可用于計算類集合的平均二分類指標,每個二分類指標可以應用于某些領域中。如果需要,可以使用average參數進行定義。
- “weighted”(權重)處理類的不均衡問題。按其在真實數據中的加權計算每個類的分數,并計算各二分類指標的平均值。
- “micro”(微)對于所有二分類指標(除非已分配樣本權重)指定給每個樣本類匹配相等的貢獻。除了匯總每個類的指標,還要匯總除數和被除數,將每個類的各指標匯總成一個整體商(總被除數/總除數得出評估模型整體水平的商)。微-平均方法更適合多標簽分類中,包括多類別分類問題,但多數類會被忽略。
- “samples”(樣本)僅應用于多標簽問題。它不對子類進行計算,而是計算評估數據中每個樣本真實類別和預測類別的指標。最后返回它們的(sample_weight - weighted)均值。
- 設置參數
average = None會返回每個類得分的數組。
當多分類數據作為類標簽數組提供給指標時,如二分類標簽,多標簽數據就會被指定為一個指標矩陣。如元素(一個列表形式)[i, j],如果樣本i被標記為j,則其值為1,否則為0。
2.2 準確率評分
accuracy_score函數計算accuracy(準確率),或者是個分數(初始值)或者是正確預測個數的計數(normalize=False)。
在多標簽分類中,函數返回各子集的準確率。如果整個集合中每一個樣本的預測標簽嚴格匹配集合中的標簽真實值,子集的準確率是1.0;否則是0.0。
如果y^i\hat{y}_iy^?i?是第i個樣本的預測值與真實值yiy_iyi?相一致,對nsamplesn_{samples}nsamples?
個樣本正確預測的分數值是:
accuracy(y,y^)=1nsamples∑i=0nsamples?11(y^i=yi)\text{accuracy}(y, \hat{y}) = \frac{1}{n_{\text{samples}}} \sum_{i=0}^{n_{\text{samples}}-1} 1(\hat{y}_i = y_i) accuracy(y,y^?)=nsamples?1?i=0∑nsamples??1?1(y^?i?=yi?)
其中*1(x)*是指標函數(indicator function)。
>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
>>> accuracy_score(y_true, y_pred, normalize=False)
2
在帶有二分類標簽指標的多標簽例子中:
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5
2.3 平衡的準確率評分(Balanced accuracy score)
balanced_accuracy_score函數計算balanced accuracy,避免了對不平衡數據集進行夸大的性能估計。每個類別召回率的宏平均,或者等同于每個樣本根據真實類別的比率(inverse prevalence)的權重,而計算的原始準確率。因此,對于平衡樣本,平衡的準確率評分(Balanced accuracy score)與準確率相同。
在二分類的例子中,平衡的準確率與靈敏度(sensitivity)相同(真正率)和特異性(specificity)(真負率),或者ROC曲線的面積(二分類預測值而不是分數):
balanced-accuracy=12(TPTP+FN+TNTN+FP)\text{balanced-accuracy} = \frac{1}{2}\left(\frac{TP}{TP + FN} + \frac{TN}{TN + FP}\right) balanced-accuracy=21?(TP+FNTP?+TN+FPTN?)
如果分類器在每個類的表現都很好,則該函數會退化為傳統的準確率(例如:正確預測的個數除以總預測樣本數)。
與之相對比,如果傳統的準確率高于樣本比例,僅因為分類器利用的是不均衡測試集,而對于平衡的準確率,會下降為
1nclasses\frac{1}{n_{\text{classes}}} nclasses?1?
分數范圍為0-1,或者當參數adjusted=True時,范圍變為
11?nclasses\frac{1}{1 - n_{\text{classes}}} 1?nclasses?1?
到1,包括邊界的,隨機得分表現為0。
如果yiy_iyi?是第i個樣本的真實值,wiw_iwi?是對應的樣本權重,從而調整的樣本權重為:
w^i=wi∑j1(yj=yi)wj\hat{w}_i = \frac{w_i}{\sum_j 1(y_j = y_i) w_j} w^i?=∑j?1(yj?=yi?)wj?wi??
其中,l(x)l(x)l(x)是指標函數。根據樣本i的預測值y^i\hat{y}_iy^?i?,平衡的準確率被定義如下:
balanced-accuracy(y,y^,w)=1∑w^i∑i1(y^i=yi)w^i\text{balanced-accuracy}(y, \hat{y}, w) = \frac{1}{\sum \hat{w}_i} \sum_i 1(\hat{y}_i = y_i) \hat{w}_i balanced-accuracy(y,y^?,w)=∑w^i?1?i∑?1(y^?i?=yi?)w^i?
設置adjusted=True,平衡的準確率報告的是比w^i=wi∑j1(yj=yi)wj\hat{w}_i = \frac{w_i}{\sum_j 1(y_j = y_i) w_j}w^i?=∑j?1(yj?=yi?)wj?wi??相對高的值。在二分類的例子中,也被稱為Youden’s J statistic或者informedness。
**注意:**多分類的定義看起來是用于二分類指標的合理延伸,盡管在文獻中未達成共識。
- 我們的定義:[Mosley2013],[Kelleher2015]和[Guyon2015],其中[Guyon2015]適合調整的版本,以確保隨機預測值為0,好的預測值為1。
- 類的均衡準確率在[Mosley2013]中描述:每個類別中精確率和召回率的最小值會被計算。將計算出的這些值進行平均,從而得到均衡的準確率。
- 均衡的準確率在[Urbanowicz2015]中被描述:每一個類別的靈敏度和特異性的均值會被計算,隨后計算總的均值。
2.4 Cohen’s kappa
cohen_kappa_score函數計算Cohen’s kappa統計值。此度量旨在比較不同標注的標簽,而分類器和真實數據的比較。
Kappa score(參見文檔字符串)是一個數值,介于-1和1之間。分數大于0.8會被認為是好的協議;小于0說明沒有協議(等同于隨機標簽)。
Kappa score可被用于計算二分類或者多分類的問題,但不適用于多標簽的問題(除手動計算每一個標簽分數)和多于兩個以上注釋器的問題。
>>> from sklearn.metrics import cohen_kappa_score
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> cohen_kappa_score(y_true, y_pred)
0.4285714285714286
2.5 混淆矩陣
confusion_matrix函數評估分類模型準確率,通過計算每一行相對應真實類別(維基百科或者其它資料可能使用不同的軸向)的混淆矩陣(confusion matrix)。
根據定義,混淆矩陣中的條目ij是實際為i,但是預測為j的觀測個數。
如下示例:
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],[0, 0, 1],[1, 0, 2]])
plot_confusion_matrix可被用于展示混淆矩陣的可視化,在混淆矩陣的例子中,如下圖所示:
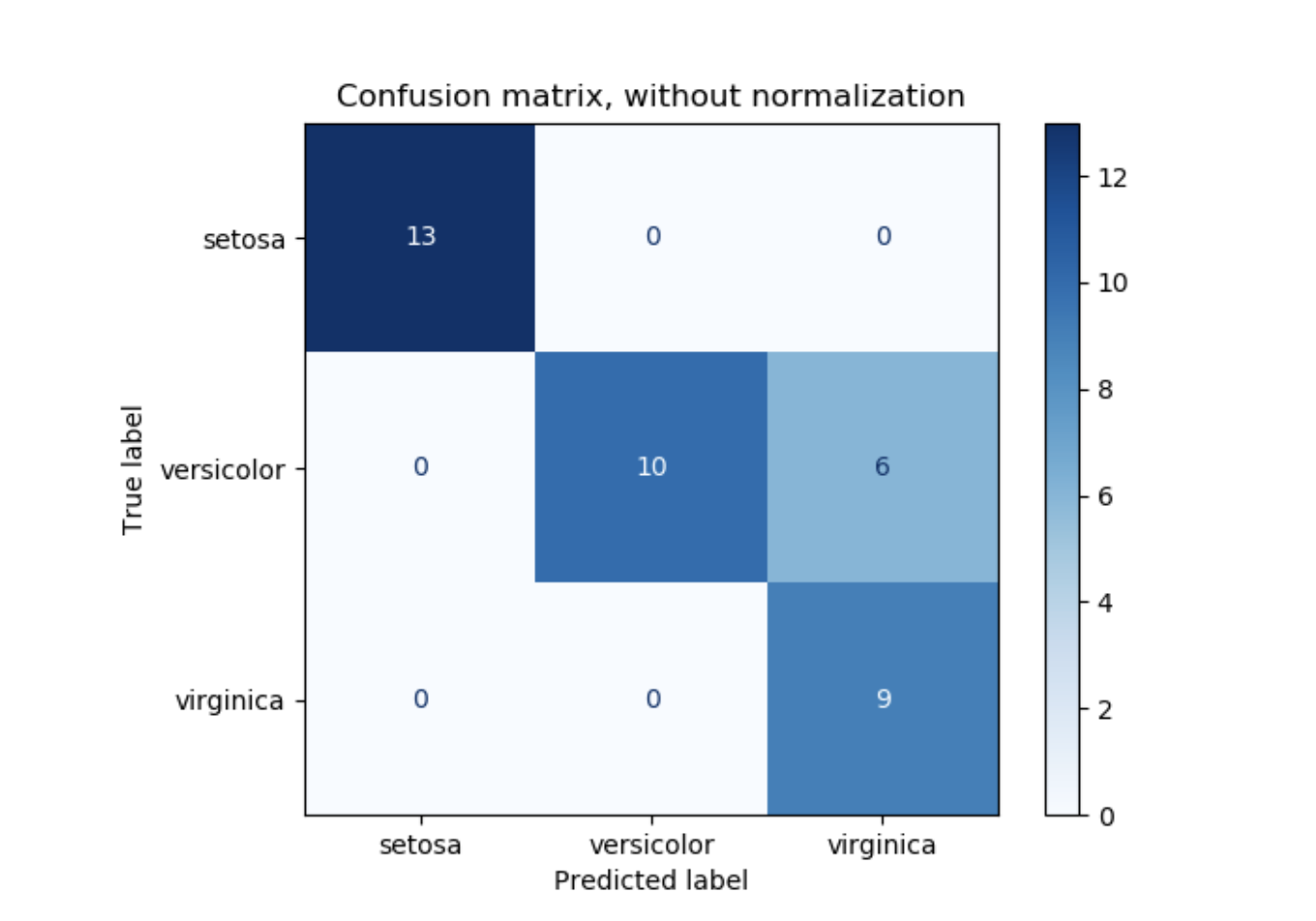
參數normalize允許報告比例而不僅是計數。混淆矩陣可以通過3種方式被規范化:“pred”, “true”, 和"all",這些參數將計算方式區分為按列求和,按行求和,或者整個矩陣求和。
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],[0.25 , 0.375]])
對于二分類問題,可以得到真負值計數,假正值計數,假負值計數和真正值計數,詳見如下代碼:
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
>>> tn, fp, fn, tp
(2, 1, 2, 3)
2.6 分類模型報告
classification_report函數輸出一個文本報告,顯示主要分類模型的評估指標。如下是一個自定義target_names和推斷標簽的例子:
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))precision recall f1-score supportclass 0 0.67 1.00 0.80 2class 1 0.00 0.00 0.00 1class 2 1.00 0.50 0.67 2accuracy 0.60 5macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
2.7 Hamming損失函數
Hamming_loss 計算平均的 Hamming loss 或者 Hamming distance 在兩個樣本的集合中。
如果 y^j\hat{y}_jy^?j? 是某個樣本第 jjj 個標簽的預測值,yjy_jyj? 是其對應的真實值,
nlabels\text{nlabels}nlabels
是類別或者標簽個數,Hamming 損失函數 LHammingL_{\text{Hamming}}LHamming? 介于兩個樣本之間:
LHamming(y,y^)=1nlabels∑j=0nlabels?11(y^j≠yj)L_{\text{Hamming}}(y, \hat{y}) = \frac{1}{n_{\text{labels}}} \sum_{j=0}^{n_{\text{labels}}-1} 1(\hat{y}_j \neq y_j) LHamming?(y,y^?)=nlabels?1?j=0∑nlabels??1?1(y^?j?=yj?)
其中,l(x) 是指標函數(indicator function)。
>>> from sklearn.metrics import hamming_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> hamming_loss(y_true, y_pred)
0.25
在二分類標簽指標的多分類標簽中:
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2)))
0.75
注意: 在多分類的分類模型中,y_true 和 y_pred 的 Hamming 損失函數與 Hamming 距離相一致。Hamming 損失函數與零一損失函數(Zero one loss)相類似。但是零一損失函數懲罰預測集合,預測集不與真實值集直接匹配;Hamming 損失函數懲罰單個標簽。因此,Hamming 損失函數的上限是零一損失函數,它介于零和一之間,包括邊界;預測真實標簽合適的子集或者超子集會使 Hamming 損失函數界于零和一之間,不包括邊界。
2.8 精確率,召回率和F-measures
直觀地說,精確率(precision)是模型區分的能力,而不是將樣本為負的標簽標記為正,而召回率(recall)是找到正樣本的能力。
F-measure(FβF\betaFβ 和 F1F1F1 測量)可被解釋為精確率和召回率的權重調和平均數。FβF\betaFβ 測量值最高為 1,最差為 0。當 β=1\beta = 1β=1 時,FβF\betaFβ 和 F1F1F1 是相等的,并且召回率和精確率是同等重要的。
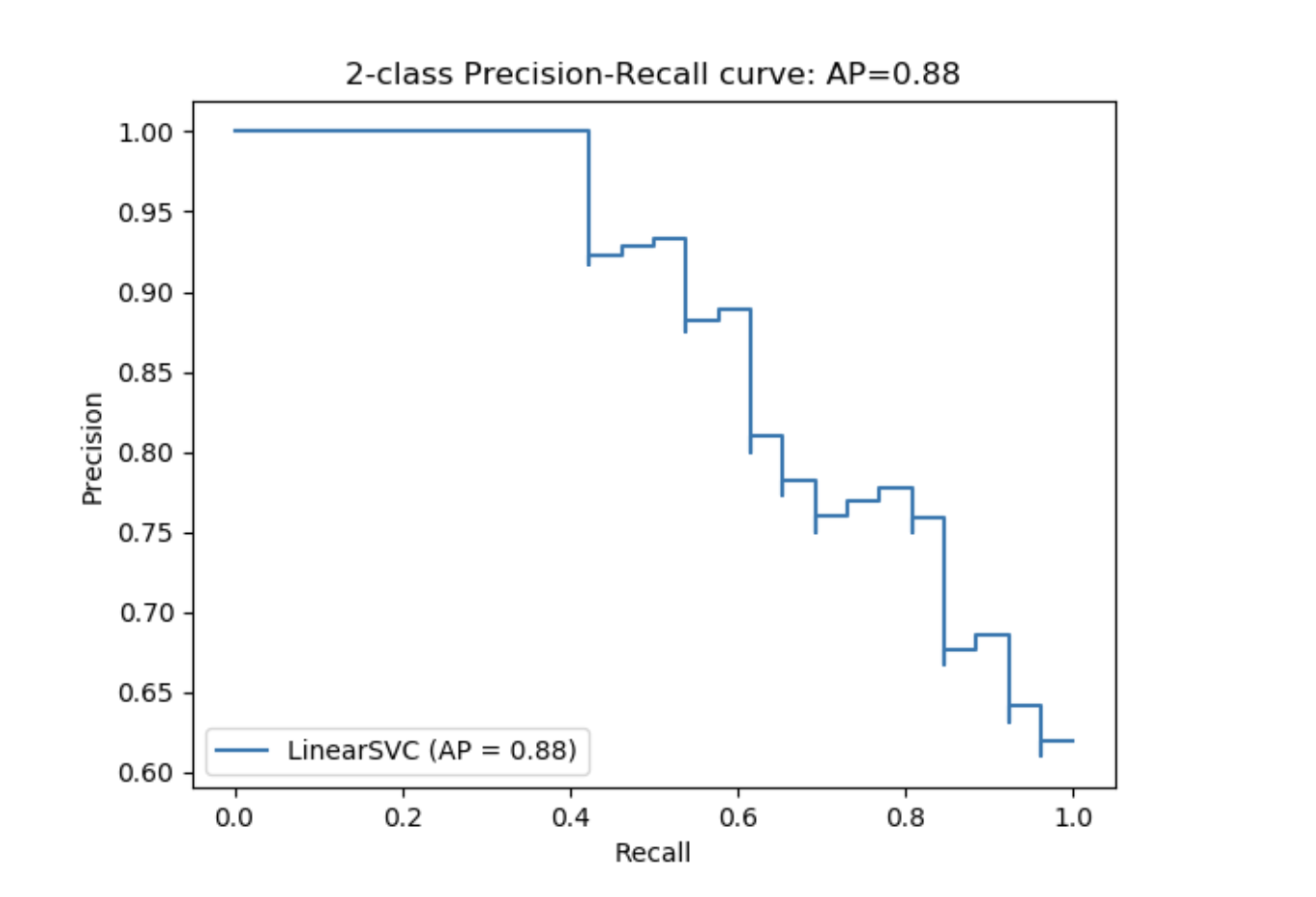
precision_recall_curve 從真實標簽和評分(不同閾值設定下,分類器的評分)計算一個精確率-召回率曲線。
average_precision_score 函數從預測分數中計算平均精確率(average precision (AP))。該值介于 0 和 1 之間,且越高越好。AP 的定義如下:
AP=∑n(Rn?Rn?1)Pn\text{AP} = \sum_{n}(R_n - R_{n-1})P_n AP=n∑?(Rn??Rn?1?)Pn?
其中,PnP_nPn? 和 RnR_nRn? 是在第 nnn 個閾值下的精確率和召回率,AP 是正樣本的分數。
參考 [Manning2008] 和 [Everingham2010] 展現 AP 的替代變體,它差值計算精確率-召回率曲線。目前,average_precision_score 并不能執行各種差值的變體。參考 [Davis2006] 和 [Flach2015] 描述了為何精確率-召回率曲線上點的線性插值產生的結果是過于樂觀的分類器表現測量。線性插值被用于計算帶有梯形法則的 ROC 曲線面積,即 auc。
以下函數提供對精確率、召回率和F-measure評分的解釋:
| 參數 | 解釋 |
|---|---|
average_precision_score(y_true, y_score, *) | 從預測評分中計算平均精確率 |
f1_score(y_true, y_pred, *[labels, ...]) | 計算F1評分,也被稱為均衡的F-score或F-measure |
fbeta_score(y_true, y_pred, *, beta[, ...]) | 計算F-beta評分 |
precision_recall_curve(y_true, probas_pred, *) | 計算在不同的閾值下精確率-召回率組合 |
precision_recall_fscore_support(y_true, ...) | 計算精確率、召回率、F-measure,且支持對每一類的計算 |
precision_score(y_true, y_pred, *[, ...]) | 計算精確率 |
recall_score(y_true, y_pred, *[, labels, ...]) | 計算召回率 |
需要注意的是:precision_recall_curve 函數只能用于二分類的例子中。average_precision_score 函數可以用于二分類的分類模型和多標簽形式。plot_precision_recall_curve 函數畫出精確率召回率關系圖,如下所示。
2.8.1 二分類分類模型
在二分類分類模型中,分類預測中的“正”和“負”,“真”和“假”指的是預測值是否與外部評判(也作“觀測值”)相一致。基于這些定義,可以總結一下表格:
| 預測類別(期望) | 實際類別(觀測值) | 實際類別(觀測值) |
|---|---|---|
| tp(真正)正確的結果 | fp(假正)意料外的結果 | |
| fn(假負)錯誤的結果 | tn(真負)正確未出現的結果 |
基于上文,可以定義精確率、召回率和F-measure的概念:
precision=tptp+fprecall=tptp+fnFβ=(1+β2)precision×recallβ2?precision+recall\begin{align*} \text{precision} &= \frac{tp}{tp + fp} \\ \text{recall} &= \frac{tp}{tp + fn} \\ F_\beta &= (1 + \beta^2) \frac{\text{precision} \times \text{recall}}{\beta^2 \cdot \text{precision} + \text{recall}} \end{align*} precisionrecallFβ??=tp+fptp?=tp+fntp?=(1+β2)β2?precision+recallprecision×recall??
如下是二分類分類模型代碼示例:
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=0.5)
0.83...
>>> metrics.fbeta_score(y_true, y_pred, beta=1)
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=2)
0.55...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5)
(array([0.66..., 1. ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2]))>>> import numpy as np
>>> from sklearn.metrics import precision_recall_curve
>>> from sklearn.metrics import average_precision_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> precision, recall, threshold = precision_recall_curve(y_true, y_scores)
>>> precision
array([0.66..., 0.5 , 1. , 1. ])
>>> recall
array([1. , 0.5, 0.5, 0. ])
>>> threshold
array([0.35, 0.4 , 0.8 ])
>>> average_precision_score(y_true, y_scores)
0.83...
2.8.2 多分類和多標簽分類模型
在多分類和多標簽分類任務中,精確率,召回率,和F-measures的定義可以應用于每一個獨立的標簽。有很多方法可以將各標簽的結果進行組合,可用average參數分別在average_precision_score(僅用于多標簽),f1_score,fbeta_score,precision_recall_support,precision_score和recall_score函數中傳遞,已在以上描述(above)。需要注意的是:如果所有的標簽啊都包括在內,那么"micro"-averaging(“微”-平均)在多分類中的設置將產生精確率,召回率和F與準確率的結果相等。也要注意"權重"平均可能產生不介于精確率和召回率之間的F-score。
為了更清晰的了解,請考慮如下概念:
- yyy 是預測值(樣本, 標簽)組合的集合
- y^\hat{y}y^? 是真實值(樣本, 標簽)組合的集合
- LLL 是標簽的集合
- SSS 是樣本的集合
- ysysys 是 yyy 的樣本 sss 的子集,例如: ys:={(s′,l)∈y∣s′=s}ys := \{(s', l) \in y | s' = s\}ys:={(s′,l)∈y∣s′=s}
- ylylyl 是 yyy 的標簽 lll 的子集
- 同樣地,ys^\hat{ys}ys^? 和 yl^\hat{yl}yl^? 均是 y^\hat{y}y^? 的子集
- P(A,B):=∣A∩B∣∣A∣P(A, B) := \frac{|A \cap B|}{|A|}P(A,B):=∣A∣∣A∩B∣?
- R(A,B):=∣A∩B∣∣B∣R(A, B) := \frac{|A \cap B|}{|B|}R(A,B):=∣B∣∣A∩B∣? (在處理 B=?B=\emptysetB=? 時,公約有所不同;這個執行使用 R(A,B):=0R(A, B):=0R(A,B):=0,并且與 PPP 類似)
- Fβ(A,B):=(1+β2)P(A,B)×R(A,B)β2P(A,B)+R(A,B)F_\beta(A, B) := (1 + \beta^2) \frac{P(A, B) \times R(A, B)}{\beta^2 P(A, B) + R(A, B)}Fβ?(A,B):=(1+β2)β2P(A,B)+R(A,B)P(A,B)×R(A,B)?
各指標定義如下:
| average | Precision | Recall | F_beta |
|---|---|---|---|
| “micro” | P(y,y^)P(y, \hat{y})P(y,y^?) | R(y,y^)R(y, \hat{y})R(y,y^?) | Fβ(y,y^)F_\beta(y, \hat{y})Fβ?(y,y^?) |
| “samples” | 1∣S∣∑s∈SP(ys,ys^)\frac{1}{|S|} \sum_{s \in S} P(ys, \hat{ys})∣S∣1?∑s∈S?P(ys,ys^?) | 1∣S∣∑s∈SR(ys,ys^)\frac{1}{|S|} \sum_{s \in S} R(ys, \hat{ys})∣S∣1?∑s∈S?R(ys,ys^?) | 1∣S∣∑s∈SF(ys,ys^)\frac{1}{|S|} \sum_{s \in S} F(ys, \hat{ys})∣S∣1?∑s∈S?F(ys,ys^?) |
| “macro” | 1∣L∣∑l∈LP(yl,yl^)\frac{1}{|L|} \sum_{l \in L} P(yl, \hat{yl})∣L∣1?∑l∈L?P(yl,yl^?) | 1∣L∣∑l∈LR(yl,yl^)\frac{1}{|L|} \sum_{l \in L} R(yl, \hat{yl})∣L∣1?∑l∈L?R(yl,yl^?) | 1∣L∣∑l∈LF(yl,yl^)\frac{1}{|L|} \sum_{l \in L} F(yl, \hat{yl})∣L∣1?∑l∈L?F(yl,yl^?) |
| “weighted” | 1∑l∈L∣yl^∣∑l∈L∣yl^∣P(yl,yl^)\frac{1}{\sum_{l \in L} |\hat{yl}|} \sum_{l \in L} |\hat{yl}| P(yl, \hat{yl})∑l∈L?∣yl^?∣1?∑l∈L?∣yl^?∣P(yl,yl^?) | 1∑l∈L∣yl^∣∑l∈L∣yl^∣R(yl,yl^)\frac{1}{\sum_{l \in L} |\hat{yl}|} \sum_{l \in L} |\hat{yl}| R(yl, \hat{yl})∑l∈L?∣yl^?∣1?∑l∈L?∣yl^?∣R(yl,yl^?) | 1∑l∈L∣yl^∣∑l∈L∣yl^∣F(yl,yl^)\frac{1}{\sum_{l \in L} |\hat{yl}|} \sum_{l \in L} |\hat{yl}| F(yl, \hat{yl})∑l∈L?∣yl^?∣1?∑l∈L?∣yl^?∣F(yl,yl^?) |
| None | $\langle P(yl, \hat{yl}) | l \in L \rangle$ | $\langle R(yl, \hat{yl}) |
>>> from sklearn import metrics >>> y_true = [0, 1, 2, 0, 1, 2] >>> y_pred = [0, 2, 1, 0, 0, 1] >>> metrics.precision_score(y_true, y_pred, average='macro') 0.22... >>> metrics.recall_score(y_true, y_pred, average='micro') 0.33... >>> metrics.f1_score(y_true, y_pred, average='weighted') 0.26... >>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5) 0.23... >>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None) (array([0.66..., 0. , 0. ]), array([1., 0., 0.]), array([0.71..., 0. , 0. ]), array([2, 2, 2]...))對于帶有“負類”的多分類類別,可以除去一些標簽:
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro')
... # excluding 0, no labels were correctly recalled
0.0
同樣地,一些未在樣本中出現的標簽,可以考慮使用宏-平均(macro-averaging)。
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro')
0.166...
未完待續、、、、


Ubuntu環境配置)

:xml.dom.minidom模塊高階使用方法)


)
)


的核心板)






深度解析)
