知識點回顧
- 序列數據的處理:
- 處理非平穩性:n階差分
- 處理季節性:季節性差分
- 自回歸性無需處理
- 模型的選擇
- AR(p) 自回歸模型:當前值受到過去p個值的影響
- MA(q) 移動平均模型:當前值收到短期沖擊的影響,且沖擊影響隨時間衰減
- ARMA(p,q) 自回歸滑動平均模型:同時存在自回歸和沖擊影響
昨天說了數據的檢驗,需要做自相關性檢驗、平穩性檢驗、季節性檢驗。
我們用了三種核心的診斷工具:
- 自相關性檢驗 (ACF/PACF圖):檢查數據點之間是否存在內在的、延遲的關聯。
- 平穩性檢驗 (ADF檢驗):判斷數據的統計特性(如均值、方差)是否隨時間改變。
- 季節性檢驗 (肉眼觀察或季節性分解):識別數據中是否存在固定的周期性波動。
那么如果數據存在某些特性需要如何處理呢?
我們的核心目標是讓數據變得平穩。為什么平穩性如此重要?因為絕大多數經典的時間序列模型(比如ARIMA模型)都建立在一個基本假設之上:數據的統計特性是恒定的。如果數據不平穩,就像一個人的脾氣陰晴不定,模型就很難抓住其規律,預測自然也就不準了。
我們今天會針對兩大“病癥”進行處理:非平穩性和季節性。而自相關性,我們則需要換個思路,它不是一個要消除的“病癥”,反而是我們要利用的“特征”,我們最后會講到。
一、序列數據的處理
處理非平穩性
通過昨天的ADF檢驗,我們發現p值顯著大于0.05,這表明數據是非平穩的。通常,這意味著數據存在趨勢(Trend),比如股價長期來看在上漲,或者銷量逐年遞增。
核心療法:差分 (Differencing)
差分是解決趨勢性問題的最強有力的工具。它的思想非常簡單:用后一個時間點的值減去前一個時間點的值。這樣做的效果是,它消除了數據在“水平”上的變化,轉而關注數據“變化的速度”。
一階差分
diff1?=yt??yt?1?
這通常能有效地消除線性的趨勢。
如果一階差分后數據仍然不平穩怎么辦?那就再做一次!
二階差分
diff2?=diff1t???diff1t?1??=(yt??yt?1?)?(yt?1??yt?2?)
這可以處理更復雜的(例如,曲線形的)趨勢。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf# 設置中文字體,防止matplotlib顯示亂碼
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 1. 生成一段非平穩數據(隨機游走+趨勢)
np.random.seed(42)
# 隨機游走部分
random_walk = np.random.randn(500).cumsum() # 累積和生成隨機游走
# 添加一個線性趨勢
trend = np.linspace(0, 100, 500)
# 合成我們的時序數據
data = pd.Series(random_walk + trend)
data.index = pd.date_range(start='2022-01-01', periods=500)隨機游走(Random Walk)是一種數學模型,常用于描述隨機過程中的路徑變化。在隨機游走模型中,每一步的方向和大小都是隨機確定的,且與之前的步驟相互獨立。這種模型可以用來模擬股票價格、分子運動、賭博結果等具有不確定性的現象。
上述代碼為了合成一個具有趨勢性和隨機性的時間序列,它結合了隨機游走和線性趨勢的特征
# 2. 診斷原始數據
plt.figure(figsize=(12, 6))plt.plot(data)
plt.title('原始數據(有明顯趨勢)')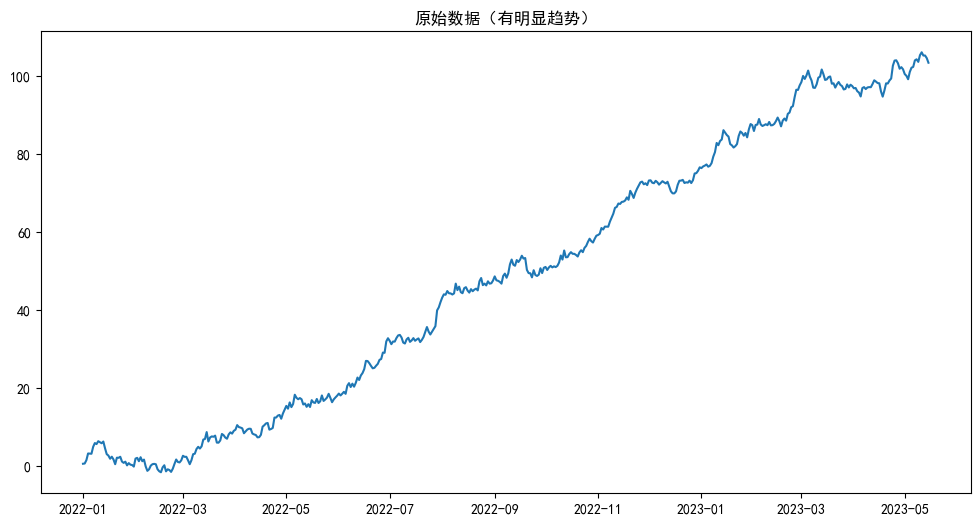
# ADF檢驗
adf_result_original = adfuller(data)
print(f'原始數據的ADF檢驗結果:')
print(f' ADF Statistic: {adf_result_original[0]}')
print(f' p-value: {adf_result_original[1]}') # p-value會非常大,說明是非平穩的#Text(0.5, 1.0, '原始數據(有明顯趨勢)')# 原始數據的ADF檢驗結果:
# ADF Statistic: 0.13578365336168233
# p-value: 0.9684209812957272# 3. 進行一階差分治療
data_diff = data.diff().dropna() # .diff()進行差分, .dropna()移除第一個NaN值plt.plot(data_diff)
plt.title('一階差分后的數據')
plt.tight_layout()
plt.show()# 4. 診斷“治療后”的數據
adf_result_diff = adfuller(data_diff)
print(f'一階差分后數據的ADF檢驗結果:')
print(f' ADF Statistic: {adf_result_diff[0]}')
print(f' p-value: {adf_result_diff[1]}') # p-value會變得非常小,說明數據變平穩了# 一階差分后數據的ADF檢驗結果:
# ADF Statistic: -22.313025583815016
# p-value: 0.0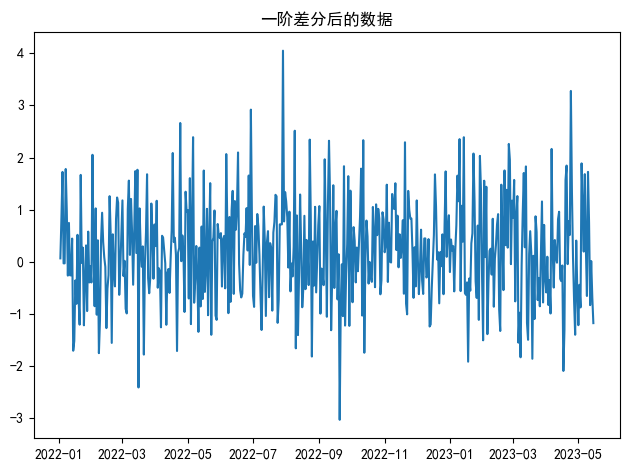
我們使用了data.diff()進行了一階差分。從圖中可以清晰地看到,原本一路向上的趨勢消失了,數據開始圍繞一個固定的均值(0附近)波動。
處理季節性
通過觀察圖像或季節性分解,我們發現數據存在以年、季度或月為單位的固定周期性波動。
核心療法:季節性差分 (Seasonal Differencing)
思想和普通差分非常類似,但不是減去上一個值,而是減去上一個周期的對應值。
seasonal_diff=yt??yt?s?
其中 ( s ) 是季節性周期。例如:
- 對于月度數據,年度季節性周期 ( s = 12 );
- 對于季度數據,年度季節性周期 ( s = 4 )。
下面生成一段帶有明顯季節性特征的數據。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller# 1. 生成一段有季節性的數據
# 假設是4年的月度數據,周期為12
time_index = pd.date_range(start='2020-01-01', periods=48, freq='M')
# 季節性成分(用sin函數模擬)
seasonal_component = np.sin(np.arange(48) * (2 * np.pi / 12)) * 10 # 振幅為10,周期為12個月,sin函數模擬季節性波動
# 趨勢成分
trend_component = np.linspace(0, 20, 48) # linspace函數為生成0到20的線性趨勢,包含48個點
# 隨機噪聲
noise = np.random.randn(48) * 2# 合成數據
seasonal_data = pd.Series(seasonal_component + trend_component + noise, index=time_index)# 2. 觀察原始數據
plt.figure(figsize=(12, 6))
plt.subplot(211)
plt.plot(seasonal_data)
plt.title('原始季節性數據')# 3. 進行季節性差分(周期s=12)
seasonal_data_diff = seasonal_data.diff(periods=12).dropna()plt.subplot(212)
plt.plot(seasonal_data_diff)
plt.title('季節性差分后 (s=12) 的數據')
plt.tight_layout()
plt.show()# 4. 檢查差分后的平穩性
# 注意:原始數據因為有趨勢,肯定不平穩。季節性差分通常也能消除一部分趨勢。
adf_result_original = adfuller(seasonal_data)
print(f'原始季節性數據的p-value: {adf_result_original[1]}')adf_result_seasonal_diff = adfuller(seasonal_data_diff)
print(f'季節性差分后數據的p-value: {adf_result_seasonal_diff[1]}')# 原始季節性數據的p-value: 0.9918566279818364
# 季節性差分后數據的p-value: 4.596236388830458e-12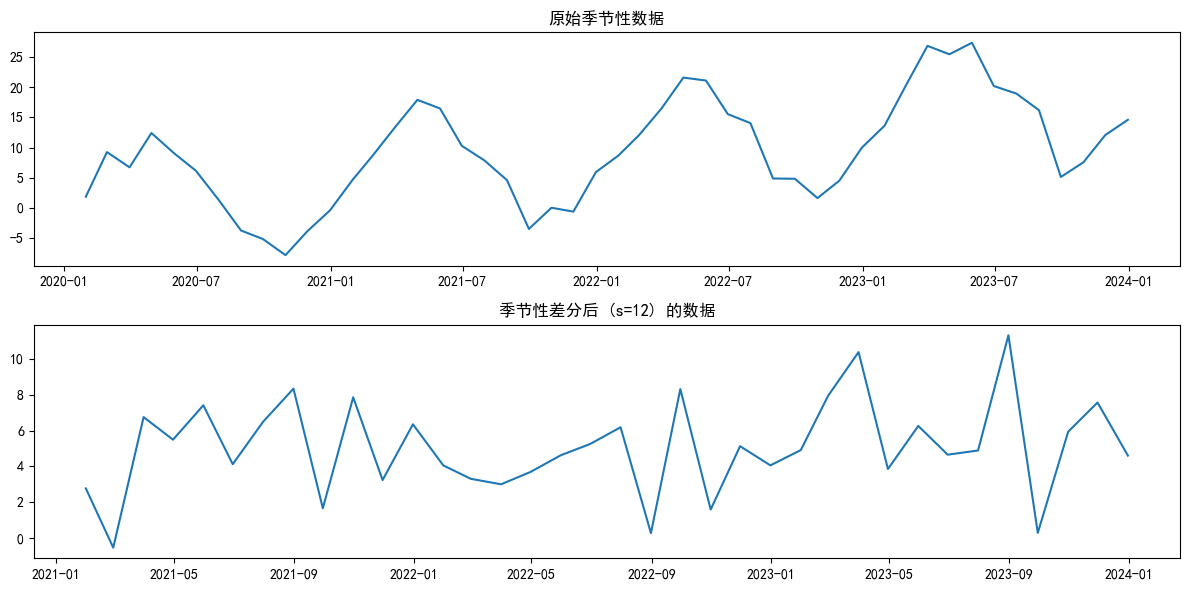
我們使用 seasonal_data.diff(periods=12),這表示每個數據點都減去它12個月前的值。從圖中可以看到,規律的波峰和波谷被“拉平”了,季節性特征被有效地移除了。
ADF檢驗的p值同樣會從一個較大的值(因為原始數據含趨勢)顯著降低,證明數據在季節性差分后變得更加平穩。
如果數據既有趨勢又有季節性,通常可以先做季節性差分,再對結果做一階差分。
目前已經學會了如何通過差分來“馴服”那些不平穩和有季節性的數據,讓它們變得溫順(平穩)。
現在,我們手上拿到了一份“健康”的平穩數據。接下來要做的,就是為它選擇一個合適的模型。我們來深入了解時間序列預測的三大基石模型:AR、MA 和 ARMA。
模型的選擇,依賴這些因素:
- ACF 圖 (自相關圖):衡量一個值和它所有過去值之間的關系,不管這些關系是直接的還是間接的。比如,Yt 和 Yt-2 的關系,也包含了 Yt-1 作為中間人的“傳話效應”。
- PACF 圖 (偏自相關圖):只衡量一個值和它某個過去值之間的直接、純粹的關系,排除了所有“中間人”的干擾。它回答的是:“在剔除了 Yt-1 的影響后, Yt-2 對 Yt 還有多少直接影響力?”
二、模型的選擇
2.1 AR模型
AR模型 (Autoregressive Model) - “慣性模型”,全稱自回歸模型,是這三個模型中最直觀的一個。
核心思想:未來是過去的延伸。一個時間點的值,很大程度上是由它緊鄰的前幾個時間點的值決定的。它認為時間序列數據具有一種“慣性”或“記憶性”。比如一只股票如果連續幾天上漲,形成上漲趨勢,那么它今天的價格也很有可能受到前幾天價格的積極影響。
AR§ 模型:表示當前值 Yt 只與它過去的 p 個值 (Yt-1, Yt-2, …, Yt-p) 有關。p 被稱為模型的“階數”
當一個序列的“慣性”是其主要特征時,AR模型是最佳選擇。我們用偵探工具來判斷:
技術指標:
- PACF 圖呈現“截尾” (Cuts off):偏自相關圖在延遲 p 階之后,突然斷崖式地落入置信區間。這說明,只有前 p 個時期的值對當前值有直接影響,更久遠的影響幾乎為零。
- ACF 圖呈現“拖尾” (Tails off):自相關圖的相關系數是緩慢、指數級下降的。這是因為 Yt-1 影響 Yt,Yt-2 影響 Yt-1,這種影響會像漣漪一樣傳遞下去,導致ACF圖緩慢衰減。
AR 模型更適合進行短期預測。因為隨著預測期的延長,模型對過去值的依賴會導致誤差不斷累積,預測的準確性會逐漸降低。比如預測未來幾天的氣溫,AR 模型可以利用過去幾天的氣溫數據進行相對準確的短期預測。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA# 設置中文字體,防止matplotlib顯示亂碼
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# --- AR(2) 案例:湖水溫度 ---
print("--- 案例一:AR(2)模型 - 湖水溫度 ---")# 1.1 生成AR(2)時間序列數據
# AR(2)模型結構:X_t = 0.7*X_{t-1} + 0.2*X_{t-2} + ε_t
# 其中ε_t是白噪聲,系數0.7和0.2控制了前兩期對當前值的影響程度
ar_params = np.array([0.7, 0.2]) # AR系數:φ?=0.7, φ?=0.2
ma_params = np.array([]) # MA部分為空(純AR模型)# 轉換為statsmodels要求的格式:
# AR系數需添加首項1并取負,即 [1, -φ?, -φ?]
ar_coeffs = np.r_[1, -ar_params] # 生成 [1, -0.7, -0.2]
# MA系數需添加首項1,即 [1, θ?, θ?, ...]
ma_coeffs = np.r_[1, ma_params] # 生成 [1.]# 創建AR(2)過程實例
ar_process = ArmaProcess(ar=ar_coeffs, ma=ma_coeffs)# 生成500個樣本點,模擬500天的湖水溫度數據
# 設置隨機種子確保結果可復現
np.random.seed(100)
ar_data = ar_process.generate_sample(nsample=500)# 1.2 時間序列分析的"偵探工作":通過可視化初步診斷模型階數
fig, axes = plt.subplots(3, 1, figsize=(10, 9))# 1.2.1 繪制原始時間序列圖
axes[0].plot(ar_data)
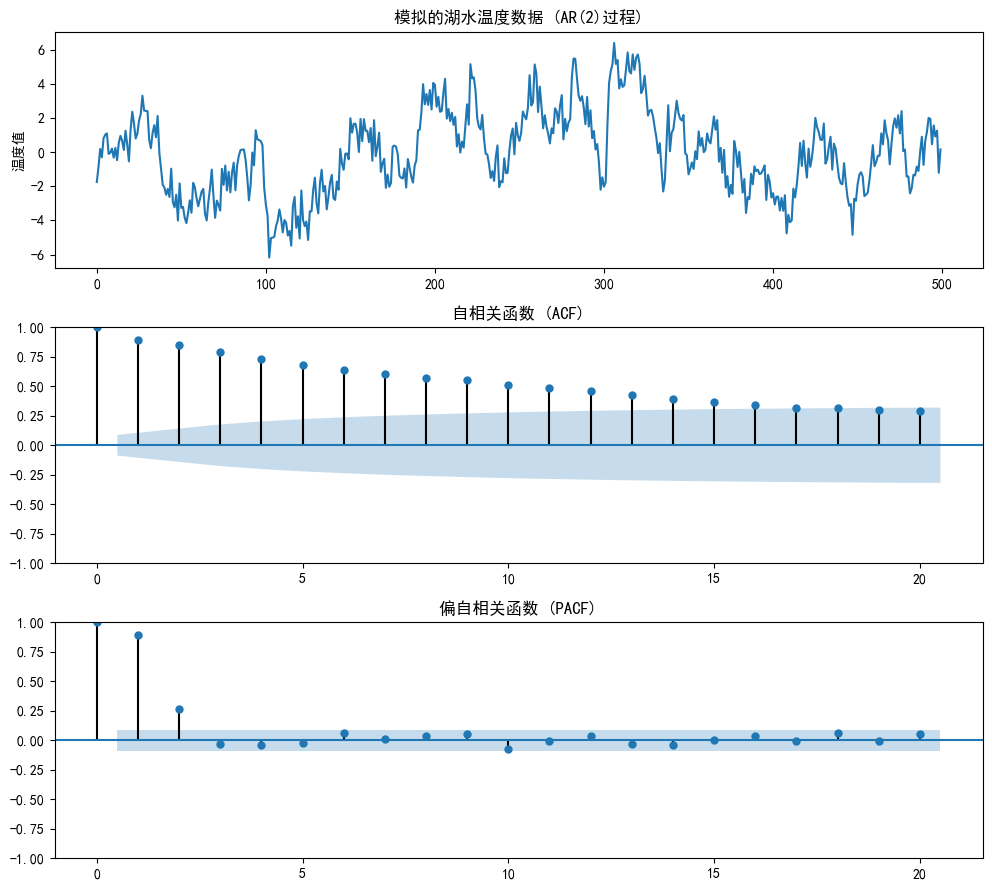
axes[0].set_title('模擬的湖水溫度數據 (AR(2)過程)')
axes[0].set_ylabel('溫度值')
# 關鍵點:觀察數據是否具有平穩性特征(均值和方差是否隨時間變化)# 1.2.2 繪制自相關函數(ACF)圖 - 衡量序列與其滯后值的相關性
plot_acf(ar_data, ax=axes[1], lags=20, title='自相關函數 (ACF)')
# 關鍵點:AR(p)模型的ACF會呈現指數衰減或周期性衰減
# 這里我們應該看到ACF在滯后2階后顯著下降# 1.2.3 繪制偏自相關函數(PACF)圖 - 控制了中間滯后項后的相關性
plot_pacf(ar_data, ax=axes[2], lags=20, title='偏自相關函數 (PACF)')
# 關鍵點:AR(p)模型的PACF會在p階后截斷(變為不顯著)
# 這里我們應該看到PACF在滯后2階后截斷,輔助確認p=2plt.tight_layout()
plt.show()--- 案例一:AR(2)模型 - 湖水溫度 ---
- 截尾(Cut-off)
定義:函數值在某一階數后突然變為 0(或在置信區間內),且之后幾乎不再顯著不為 0。
特點:存在一個明確的 “截斷點”,超過該點后相關性驟降為零。
示例:若 ACF 在 k=2 階后的值接近 0,則稱 ACF 在 2 階截尾。
- 拖尾(Tail-off)
定義:函數值隨階數增加逐漸衰減(如指數衰減、振蕩衰減),但始終不降至 0,呈現 “拖曳” 趨勢。
特點:無明確截斷點,相關性緩慢減弱,但長期保持非零。
示例:若 PACF 的值從 k=1 階開始逐漸趨近于 0,但始終大于 0,則稱 PACF 拖尾。
- PACF圖 (偏自相關圖):這是我們的關鍵證據!可以看到,在滯后1和2階,柱子非常顯著。但在2階之后,幾乎所有柱子都突然“截斷”,掉入了藍色置信區間。 這說明,只有前兩天的溫度對今天有直接影響。 PACF在2階截尾 -> 強烈暗示 p=2。
- ACF圖 (自相關圖):柱子是緩慢衰減的,呈現一種“拖尾”形態。這符合我們對“慣性”的理解,影響會層層傳遞下去。ACF拖尾,驗證了AR模型的猜想。
所以ar模型適合自回歸的場景
我們的診斷是AR(2),即 ARIMA(2,0,0)。我們來驗證一下。
ARIMA(p,d,q)其中包含3個參數,ARIMA(ar_data, order=(2, 0, 0))等價于AR(2)
# 1.3 根據ACF/PACF圖的診斷,建立ARIMA(2,0,0)模型
model_ar = ARIMA(ar_data, order=(2, 0, 0)).fit()
print("\nAR(2)模型診斷報告:")
print(model_ar.summary())
AR(2)模型診斷報告:SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 500
Model: ARIMA(2, 0, 0) Log Likelihood -724.007
Date: Thu, 26 Jun 2025 AIC 1456.014
Time: 23:22:20 BIC 1472.873
Sample: 0 HQIC 1462.629- 500
Covariance Type: opg
==============================================================================coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0971 0.578 -0.168 0.867 -1.231 1.036
ar.L1 0.6557 0.042 15.552 0.000 0.573 0.738
ar.L2 0.2646 0.043 6.096 0.000 0.180 0.350
sigma2 1.0562 0.066 16.075 0.000 0.927 1.185
===================================================================================
Ljung-Box (L1) (Q): 0.04 Jarque-Bera (JB): 3.45
Prob(Q): 0.84 Prob(JB): 0.18
Heteroskedasticity (H): 0.96 Skew: 0.19
Prob(H) (two-sided): 0.79 Kurtosis: 3.15
===================================================================================這個表的結果讓ai幫助你們解讀,信息比較多
系數顯著:模型準確地識別出前兩階的自回歸關系是統計上顯著的,并且學習到的系數值(0.66, 0.26)與真實值(0.7, 0.2)非常接近。
2.2 MA模型
數據的波動是由短期沖擊引起的(而非歷史觀測值),且沖擊影響會隨時間衰減。例如:突發事件(罷工、自然災害)對生產的影響、測量誤差。
假設一條生產線非常穩定,但偶爾會因為工人操作失誤或機器小故障(這些都是隨機沖擊/誤差)導致當天的產量出現波動。這個沖擊的影響可能只會持續一兩天。我們來創建一個MA(2)過程。
# --- MA(2) 案例:生產線意外 ---
print("\n" + "---"*15)
print("--- 案例二:MA(2)模型 - 生產線意外 ---")"""
=====================
2.1 生成MA(2)時間序列
=====================
MA(2)模型數學表達式:y_t = ε_t + θ?ε_{t-1} + θ?ε_{t-2}
- 當前值由當前及前兩期的隨機沖擊(ε)線性組合而成
- 適用于捕捉短期沖擊對序列的影響(如生產線故障、原料短缺)
"""
# AR部分參數:因無自回歸項
ar_params = np.array([])
# MA部分參數:0.8和0.4分別是前兩期沖擊的權重
ma_params = np.array([0.8, 0.4]) # 生成MA(2)過程:直接傳入AR和MA系數數組(注意無參數名)
ma_process = ArmaProcess.from_coeffs(ar_params, ma_params)# 設置隨機種子保證結果可復現,生成500個樣本點
np.random.seed(200)
ma_data = ma_process.generate_sample(nsample=500)"""
============================
2.2 可視化分析時間序列特征
============================
通過觀察ACF和PACF圖判斷模型階數:
- MA(q)模型的ACF應在q階后截尾(本例q=2)
- PACF應呈現拖尾特征(與AR模型區分)
"""
# 創建3個子圖:時間序列圖、ACF圖、PACF圖
fig, axes = plt.subplots(3, 1, figsize=(10, 9))# 繪制時間序列圖:展示生產線產量波動
axes[0].plot(ma_data)
axes[0].set_title('模擬的生產線產量波動 (MA(2)過程)')
axes[0].set_xlabel('時間點')
axes[0].set_ylabel('產量波動值')# 繪制自相關函數(ACF)圖:觀察序列相關性衰減模式
plot_acf(ma_data, ax=axes[1], lags=20, title='自相關函數 (ACF)')
# 理論預期:MA(2)的ACF應在2階后截尾(相關性驟降為0)# 繪制偏自相關函數(PACF)圖:剔除中間變量影響的直接相關性
plot_pacf(ma_data, ax=axes[2], lags=20, title='偏自相關函數 (PACF)')
# 理論預期:MA(2)的PACF應呈現拖尾(指數或振蕩衰減)# 優化子圖布局,避免重疊
plt.tight_layout()
plt.show()--------------------------------------------- --- 案例二:MA(2)模型 - 生產線意外 ---
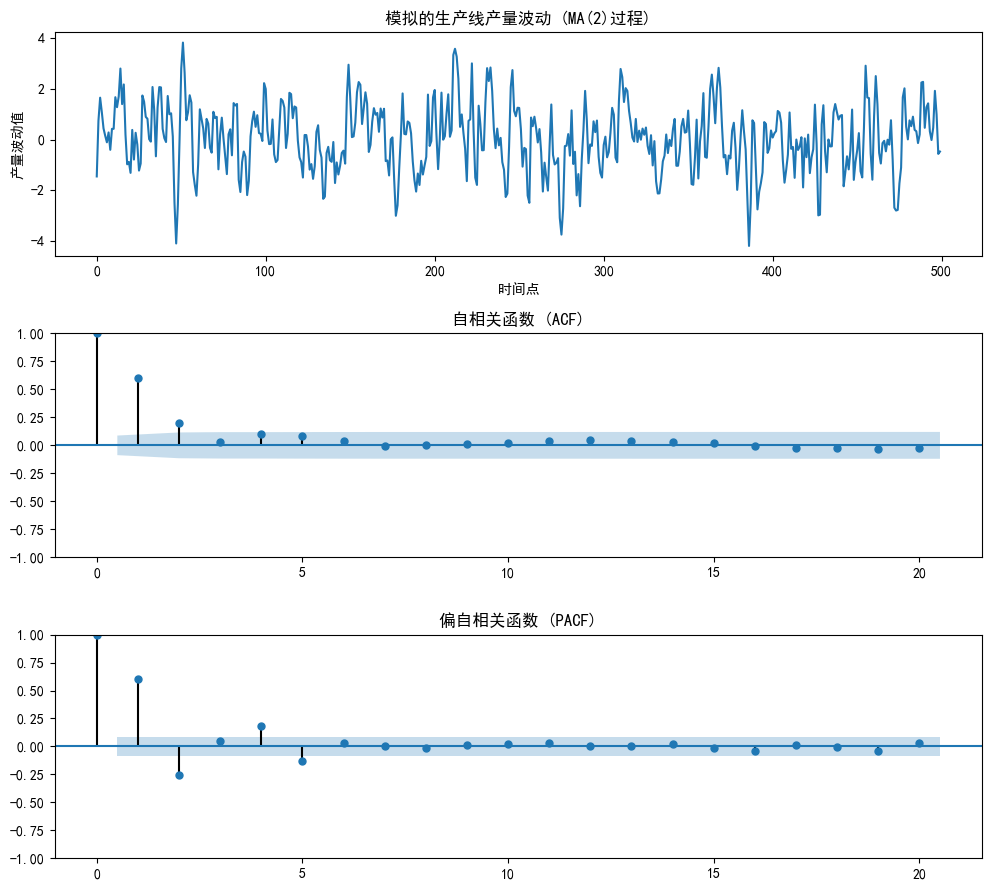
- ACF圖 (自相關圖):這次輪到ACF圖提供關鍵線索了!可以看到,在滯后1和2階,柱子非常顯著。但在2階之后,柱子突然“截斷”,掉入了置信區間。 這說明,一個隨機沖擊的影響最多只持續2天。ACF在2階截尾 -> 強烈暗示 q=2。
- PACF圖 (偏自相關圖):柱子呈現出緩慢衰減的“拖尾”形態。PACF拖尾,驗證了MA模型的猜想。
# 2.3 根據ACF/PACF圖的診斷,建立ARIMA(0,0,2)模型
model_ma = ARIMA(ma_data, order=(0, 0, 2)).fit()
print("\nMA(2)模型診斷報告:")
print(model_ma.summary())Text(0.5, 1.0, '原始數據(有明顯趨勢)')
原始數據的ADF檢驗結果:ADF Statistic: 0.13578365336168233p-value: 0.9684209812957272
一階差分后數據的ADF檢驗結果:ADF Statistic: -22.313025583815016p-value: 0.0
原始季節性數據的p-value: 0.9918566279818364
季節性差分后數據的p-value: 4.596236388830458e-12
--- 案例一:AR(2)模型 - 湖水溫度 ---AR(2)模型診斷報告:SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 500
Model: ARIMA(2, 0, 0) Log Likelihood -724.007
Date: Thu, 26 Jun 2025 AIC 1456.014
Time: 23:22:20 BIC 1472.873
Sample: 0 HQIC 1462.629- 500
Covariance Type: opg
==============================================================================coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0971 0.578 -0.168 0.867 -1.231 1.036
ar.L1 0.6557 0.042 15.552 0.000 0.573 0.738
ar.L2 0.2646 0.043 6.096 0.000 0.180 0.350
sigma2 1.0562 0.066 16.075 0.000 0.927 1.185
===================================================================================
Ljung-Box (L1) (Q): 0.04 Jarque-Bera (JB): 3.45
Prob(Q): 0.84 Prob(JB): 0.18
Heteroskedasticity (H): 0.96 Skew: 0.19
Prob(H) (two-sided): 0.79 Kurtosis: 3.15
===================================================================================Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).---------------------------------------------
--- 案例二:MA(2)模型 - 生產線意外 ---MA(2)模型診斷報告:SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 500
Model: ARIMA(0, 0, 2) Log Likelihood -704.426
Date: Thu, 26 Jun 2025 AIC 1416.852
Time: 23:26:03 BIC 1433.710
Sample: 0 HQIC 1423.467- 500
Covariance Type: opg
==============================================================================coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0582 0.100 0.584 0.559 -0.137 0.253
ma.L1 0.8252 0.041 19.978 0.000 0.744 0.906
ma.L2 0.4180 0.041 10.099 0.000 0.337 0.499
sigma2 0.9785 0.063 15.604 0.000 0.856 1.101
===================================================================================
Ljung-Box (L1) (Q): 0.42 Jarque-Bera (JB): 0.01
Prob(Q): 0.51 Prob(JB): 0.99
Heteroskedasticity (H): 1.08 Skew: -0.01
Prob(H) (two-sided): 0.62 Kurtosis: 2.99
===================================================================================模型報告中,ma.L1的系數約為0.8,ma.L2的系數約為0.4,和我們設定的參數高度吻合!p值也都極其顯著。再次成功破案!
2.3 ARMA模型
現實世界中,很多情況是混合的。比如公司月度銷售額,既有上個月業績帶來的慣性(AR成分),又會受到某次市場推廣活動或負面新聞的短期沖擊(MA成分)。我們來創建一個ARMA(1,1)過程。
# --- ARMA(1,1) 案例:公司月度銷售 ---
print("\n" + "---"*15)
print("--- 案例三:ARMA(1,1)模型 - 公司月度銷售 ---")# 3.1 我們來“創造”一個ARMA(1,1)過程
# 修復:直接傳入系數數組,并確保包含常數項
ar_params = np.array([1, -0.8]) # AR部分: [1, -φ1]
ma_params = np.array([1, 0.5]) # MA部分: [1, θ1]# 正確調用方式:直接傳入系數數組,不使用參數名
arma_process = ArmaProcess.from_coeffs(ar_params, ma_params)np.random.seed(300)
arma_data = arma_process.generate_sample(nsample=500)# 3.2 作為“偵探”,我們觀察數據和ACF/PACF圖
fig, axes = plt.subplots(3, 1, figsize=(10, 9))
axes[0].plot(arma_data)
axes[0].set_title('模擬的公司月度銷售 (ARMA(1,1)過程)')
plot_acf(arma_data, ax=axes[1], lags=20, title='自相關函數 (ACF)')
plot_pacf(arma_data, ax=axes[2], lags=20, title='偏自相關函數 (PACF)')
plt.tight_layout()
plt.show()--------------------------------------------- --- 案例三:ARMA(1,1)模型 - 公司月度銷售 ---
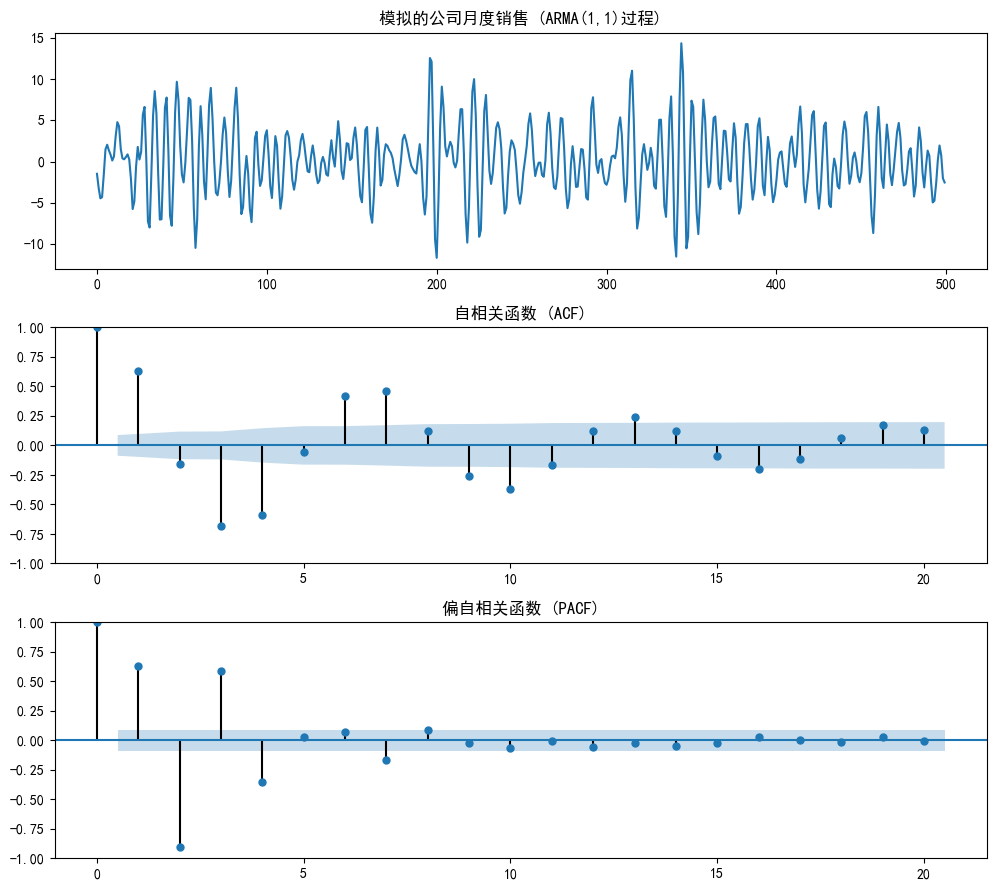
-
ACF圖 和 PACF圖:這次我們發現,情況變得復雜了。ACF圖和PACF圖都沒有出現明顯的“截尾”現象,兩者的柱子都是緩慢衰減,呈現“拖尾”形態。
解讀:當兩個圖都拖尾時,這就是一個強烈的信號,說明數據背后的驅動力是混合的,既有AR成分,也有MA成分。 -
定階:對于ARMA模型,從圖上直接確定p和q的精確值會比較困難。通常我們會從低階開始嘗試,比如(1,1), (2,1), (1,2),然后結合后續的模型評估指標(如AIC, BIC)來選擇最優的。但既然兩個圖都是拖尾,我們就先從最簡單的ARMA(1,1)開始猜起。
# 3.3 根據ACF/PACF圖的診斷,建立ARIMA(1,0,1)模型
model_arma = ARIMA(arma_data, order=(1, 0, 1)).fit()
print("\nARMA(1,1)模型診斷報告:")
print(model_arma.summary())
ARMA(1,1)模型診斷報告:SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 500
Model: ARIMA(1, 0, 1) Log Likelihood -1058.680
Date: Thu, 26 Jun 2025 AIC 2125.360
Time: 23:26:39 BIC 2142.218
Sample: 0 HQIC 2131.975- 500
Covariance Type: opg
==============================================================================coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.1610 0.393 0.410 0.682 -0.608 0.930
ar.L1 0.5656 0.035 16.047 0.000 0.496 0.635
ma.L1 0.8998 0.021 43.067 0.000 0.859 0.941
sigma2 4.0193 0.241 16.654 0.000 3.546 4.492
===================================================================================
Ljung-Box (L1) (Q): 84.33 Jarque-Bera (JB): 1.10
Prob(Q): 0.00 Prob(JB): 0.58
Heteroskedasticity (H): 1.15 Skew: -0.03
Prob(H) (two-sided): 0.36 Kurtosis: 3.22
===================================================================================模型報告中,ar.L1系數約為0.8,ma.L1系數約為0.5,都非常接近我們的設定值,且p值都為0.000。
前提:以上所有判斷都必須在數據平穩后進行!如果你的原始數據不平穩,請先做差分,然后對差分后的序列進行ACF/PACF分析。
這正是我們最終要學習的 ARIMA(p, d, q) 模型的由來,將在明天學習。
- AR§: 自回歸項,看PACF。
- I(d): 差分階數 (Integrated),看我們為了讓數據平穩做了幾次差分。
- MA(q): 移動平均項,看ACF。
總結
-
非平穩性(趨勢) -> 使用差分 (.diff())
-
季節性 -> 使用季節性差分 (.diff(periods=s))
-
自相關性 -> 不消除,而是利用 ACF/PACF圖 來為后續的模型選擇提供線索。
-
截尾 (Cut off):ACF或PACF圖在某個延遲之后,相關系數突然變得非常小,幾乎都在置信區間內。
-
拖尾 (Tail off):相關系數隨著延遲增加而緩慢、指數級地衰減,而不是突然截斷。
-
如果ACF截尾,PACF拖尾 -> 考慮 MA(q) 模型。
-
如果PACF截尾,ACF拖尾 -> 考慮 AR§ 模型。
-
如果ACF和PACF都拖尾,可能需要 ARMA(p, q) 模型。
@浙大疏錦行
)









)

到 mapMulti())


)


)
