從老Android Studio版本升級到新版Android Studio Meerkat | 2024.3.1

gradle版本從8.0升到8.9，complieSdk版本從33升到34

編譯報錯Unknown Kotlin JVM target: 21

原因：原版本中jvm版本是17

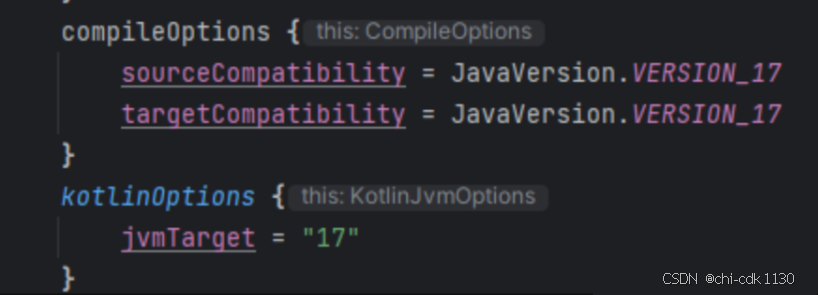
而新版studio自帶的版本就是21。

解決：

將jvm版本降回17。即按照上圖，在Gradle JDK的位置選擇[Download JDK]，選擇17版本

選擇好版本，點擊確定，再次sync，下載完成，異常修復。

ps：高版本下自定義view類中的onDraw方法可能會報錯，
將
override fun onDraw(canvas: Canvas?){}
改為
override fun onDraw(canvas: Canvas){}
即可。