-----------------------------------------------------------------------------------------------

這是我在我的網站中截取的文章，有更多的文章歡迎來訪問我自己的博客網站rn.berlinlian.cn，這里還有很多有關計算機的知識，歡迎進行留言或者來我的網站進行留言！！！

-----------------------------------------------------------------------------------------------

一、邏輯回歸代價函數的定義

邏輯回歸的代價函數（又稱交叉熵損失）用于評估模型預測結果與真實標簽之間的差異。不同于線性回歸的均方誤差，它專門針對分類問題設計，能夠有效懲罰“高置信度的錯誤預測”，同時鼓勵模型輸出更接近真實標簽的概率值。

通俗理解

想象老師在批改判斷題：

• 如果學生非常自信地答錯（比如寫“絕對選A”，但正確答案是B），老師會狠狠扣分。

• 如果學生答對但不太確定（比如寫“可能是A”），老師會適當給分。

• 如果學生答對且很確定（比如寫“肯定選A”），老師會給滿分。
  代價函數的作用類似——讓模型為自己的“盲目自信”付出代價，同時獎勵正確且確定的預測。

---

二、平方誤差 vs 邏輯回歸：代價函數的設計差異與凸性對比

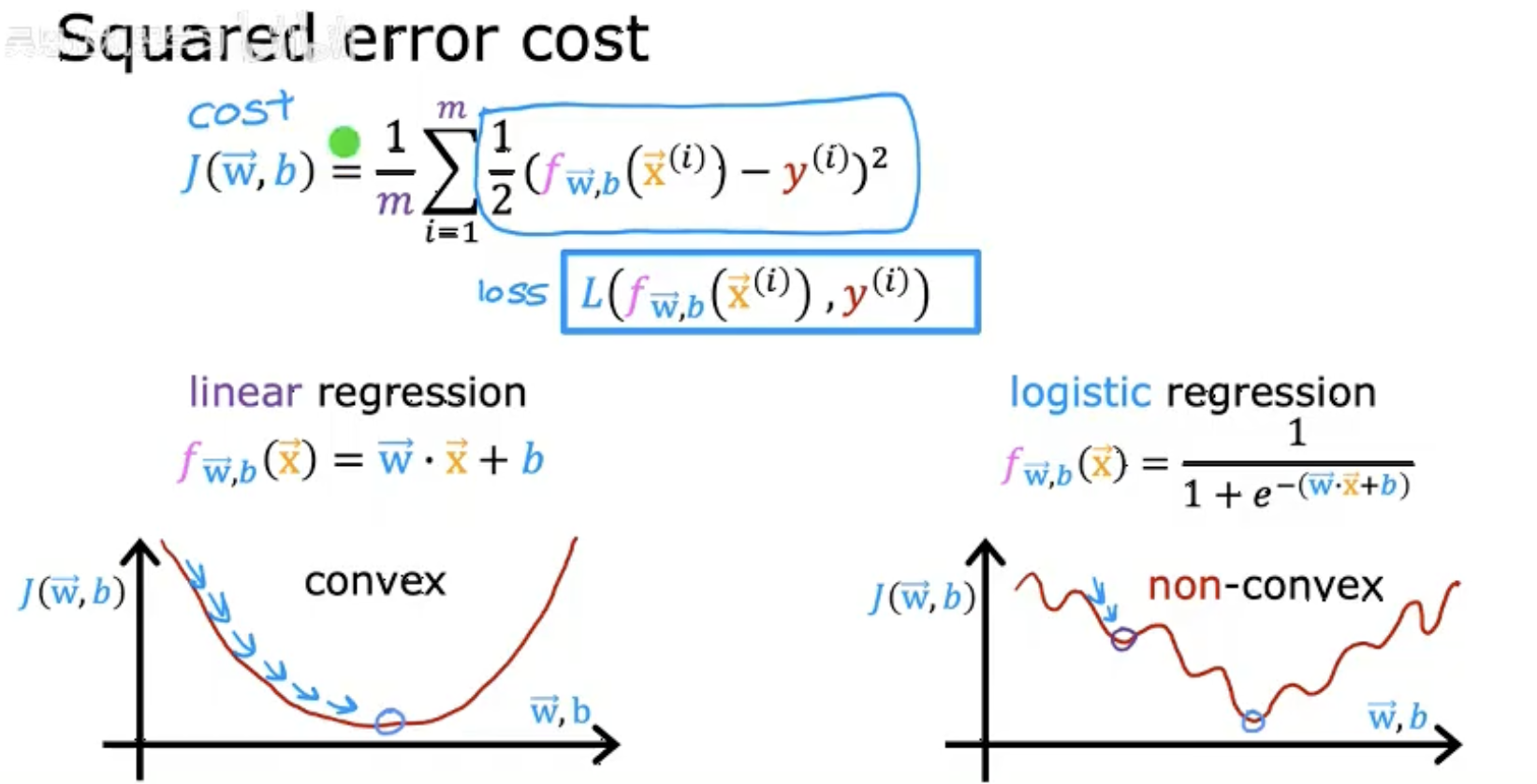
這張圖片展示了平方誤差代價函數（Squared error cost）及其相關概念，主要分為以下幾個部分：

1. 平方誤差代價函數公式：

   

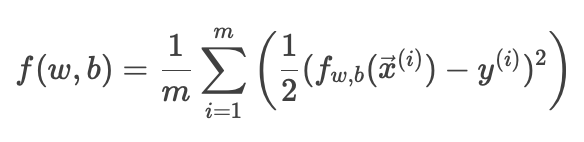
   用于衡量線性回歸模型的預測值與真實值之間的誤差。

2. 損失函數（loss）：

   

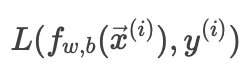
   表示單個樣本的誤差。

3. 線性回歸模型：

   

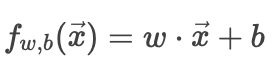
   這是一個線性預測函數。

4. 凸性與非凸性：

   • 線性回歸的代價函數?f(w,b)?是凸函數（convex），保證梯度下降能找到全局最優解。

   • 如果直接對邏輯回歸使用平方誤差，代價函數可能非凸（non-convex），導致優化困難。

5. 邏輯回歸的預測函數：

   

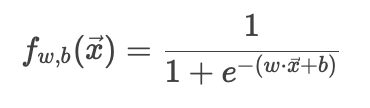
   這是一個Sigmoid函數，將線性輸出映射到概率（0, 1）。

圖片的核心對比了線性回歸（平方誤差）和邏輯回歸（需用交叉熵損失）在代價函數設計上的差異。

---

三、邏輯回歸代價函數公式

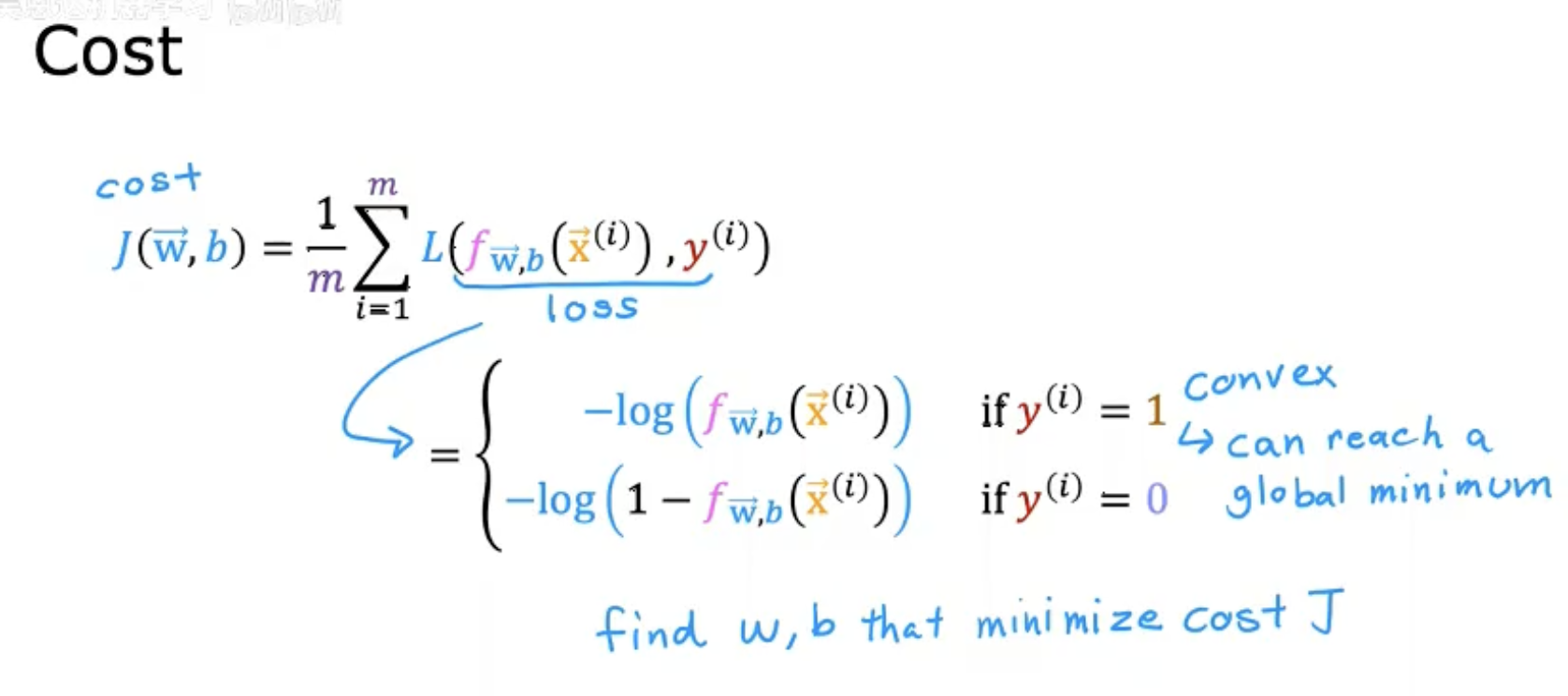
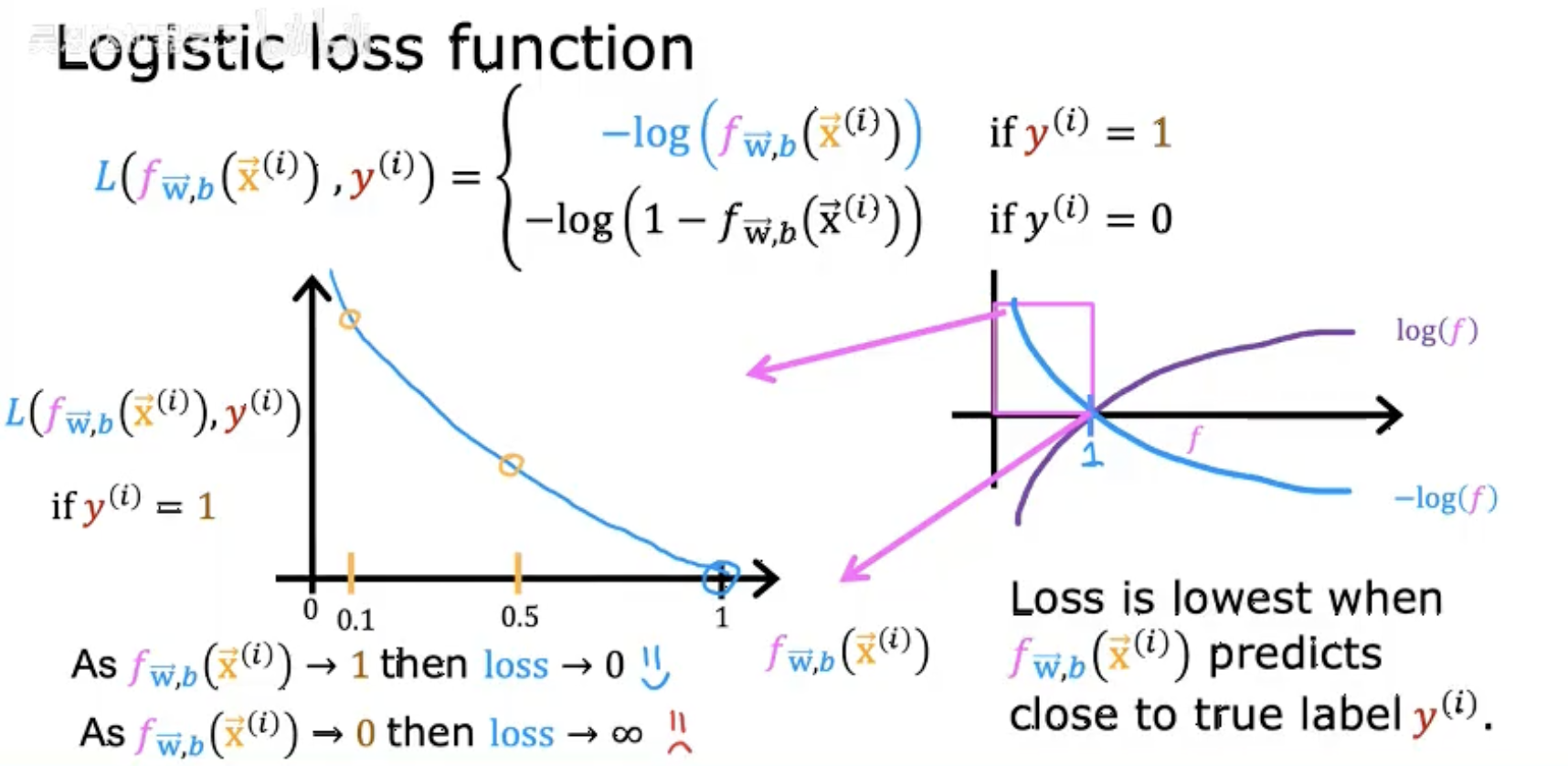
1. 分段定義：
   損失函數?L?根據真實標簽?y(i)?的取值（0 或 1）分段計算：

   • 若?y(i)=1，損失為??log?(fW,b(x?(i)))。

   • 若?y(i)=0，損失為??log?(1?fW,b(x?(i)))。

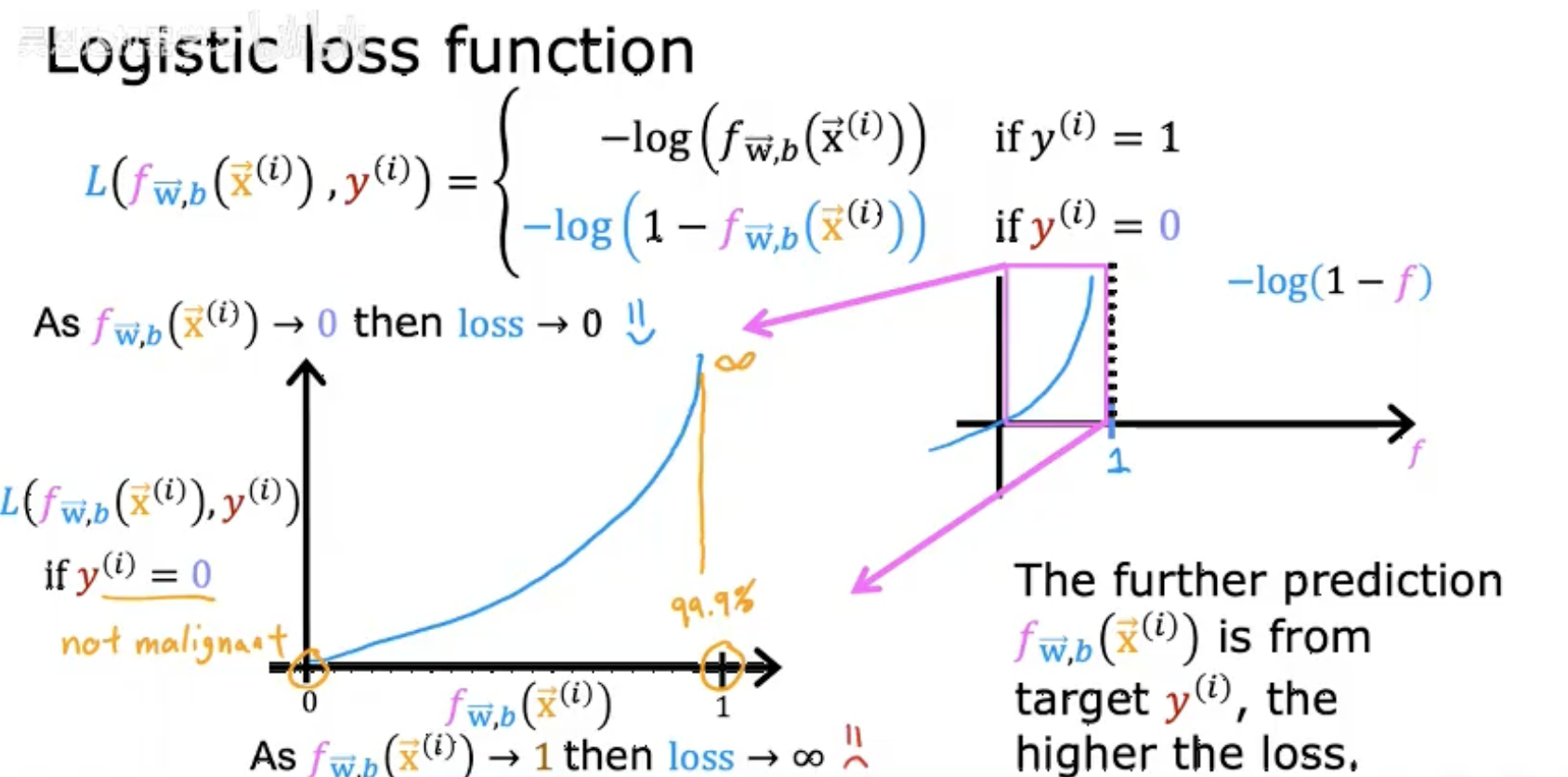
2. 損失變化趨勢：

   • 當預測值?fW,b(x?(i))?接近真實標簽時（如?y(i)=1?且?f→1），損失趨近于 0。

   • 當預測值與真實標簽相反時（如?y(i)=1?但?f→0），損失趨近于無窮大。

3. 核心作用：
   損失函數通過對數懲罰機制，迫使模型對錯誤預測（尤其是高置信度錯誤）付出更高代價，從而推動參數優化。

4. 優化目標
   通過調整參數?w?,b?最小化代價函數?J，使模型預測?fw?,b(x?)?盡可能接近真實標簽?y。

---

四、邏輯回歸損失函數的兩種表達形式及其統一化

1. 第一幅圖

   • 展示了邏輯回歸損失函數從分段形式到統一形式的簡化過程。

   • 分段形式（直觀但冗長）：

     • 當?y=1，損失為??log?(f(x))

     • 當?y=0，損失為??log?(1?f(x))

   • 統一形式（緊湊且通用）：

     

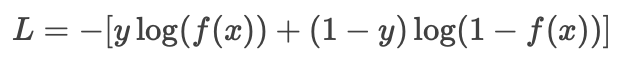
   • 通過數學技巧將兩種情況合并為一個公式，便于計算和優化。

2. 第二幅圖

   • 將單樣本的損失函數推廣到整體代價函數（所有樣本的平均損失）。

   • 公式：

     

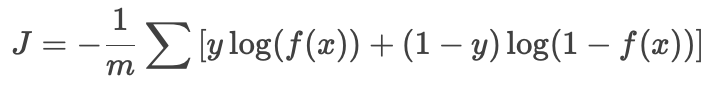
   • 強調該函數是凸函數（convex），保證梯度下降能找到全局最優解。

-----------------------------------------------------------------------------------------------

這是我在我的網站中截取的文章，有更多的文章歡迎來訪問我自己的博客網站rn.berlinlian.cn，這里還有很多有關計算機的知識，歡迎進行留言或者來我的網站進行留言！！！

-----------------------------------------------------------------------------------------------