決策樹構建：

決策樹的結構與python中的二叉樹結構(PY數據結構-樹)相似，不過決策樹中除了葉節點之外的其他節點，都被稱之為“決策節點”，構建決策樹的過程，也就是選取每一個節點采用哪一個特征作為劃分依據的過程。

以解決二元分類問題為例，最終的葉節點輸出只有兩種情況：0或1，那么在前面的每一個決策節點時我們自然希望每一個節點分支得到的樣本盡可能屬于同一個類別，也就是說得到的示例樣本純度最高。因此，我們引入“熵”的概念，熵用于衡量樣本的不純度，其表達式如下：

其中：?——所有樣本中正例的占比；

? ? ? ? ? ? ——所有樣本中負例的占比。

其圖像如上圖所示，可以看出，當一個樣本中正例和負例各占一半時，對于分類而言此時樣本是最不純的，相應的熵值取最大值1；而當一個樣本中全部為正例或負例時，對于分類而言此時樣本最純，相應的熵值取最小值0。

因此，決策節點的特征選取問題就轉變為哪一個特征作為劃分依據時可以最大程度的降低熵值的問題。并且，需要注意的一點是，當某一個分支的樣本的數量較大時，保證該分支的純度是更為重要的。這是因為樣本數量多的分支在訓練數據中占比更高，其分類結果對模型的整體準確率、召回率等指標影響更大。因此我們進一步的將特征分裂后的左右子分支得到的熵值進行加權平均計算：

熵值的減少量也被稱之為信息增益，而在實際運用中，我們一般會采取最大信息增益（也就是最大熵值降低）作為劃分依據，這與樹的停止劃分有關。信息增益計算如下：

劃分停止依據：

決策樹的停止劃分依據有如下四種：

• 該節點已經100%是某一個類別；
• 已經達到的樹的最大深度；
• 信息增益已經低于閾值；
• 節點的示例樣本已經低于閾值。

即使最終樹的葉節點沒有達到100%的純度，我們也需要通過其他依據來停止繼續劃分，因為當樹的規模過大時難以管理，并且很有可能會出現過擬合（決策樹會為了純度不斷地生成過于復雜的劃分規則）。同時，當繼續劃分得到的信息增益過小時，也沒有必要再繼續進行下去，理由同前者。

特征取值非二元：

前面提到過決策樹的結構與二叉樹相似，而如果某一個特征的取值是>2個的離散值/連續任意值時，我們需要采用一些轉換的方法來保證二叉的結構。

獨熱編碼：

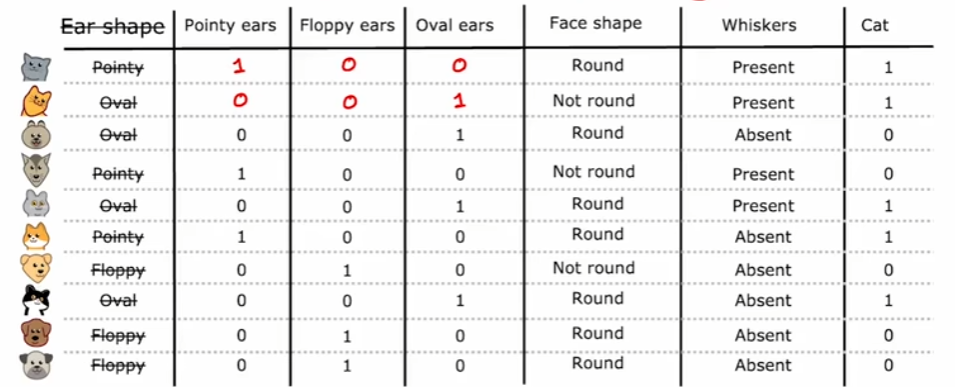
對于取值為非任意離散值時，比如在下圖的耳朵形狀特征的取值中，可取值有三類：尖耳、垂耳以及橢圓形，我們將耳朵形狀的分類變量轉換成二進制向量，如下圖所示。此時我們不再將耳朵形狀作為分類特征，而是直接將它的三個取值類別作為分類特征，相應的每個樣本在這三個分類特征中只會有一個值取1，因此稱為獨熱。

閾值分割：

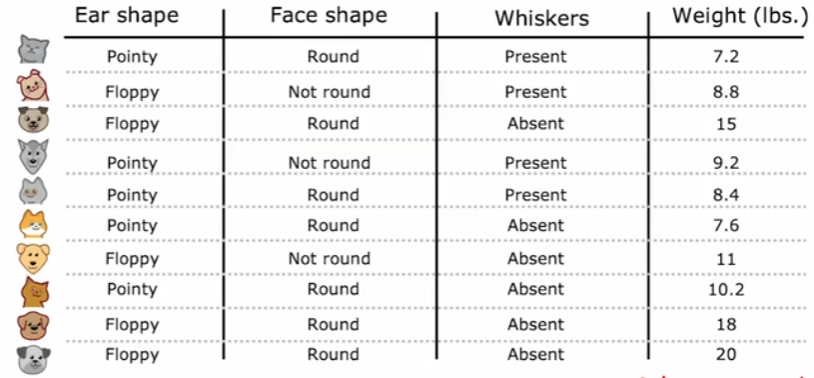
對于取值為連續任意值時，比如下圖中的體重，此時無法同上采用獨熱編碼來處理，因此一般是通過閾值分割將此特征的取值劃分為兩類作為分裂。而對于閾值的選擇，通常是將訓練樣本中所有該特征取值進行排序，再取相鄰值的中點作為候選閾值，然后計算每個候選閾值分裂后的信息增益，選擇使增益最大的閾值。這可以保證在所有訓練數據中確保找到當前特征下的全局最優分裂點，不過相應的計算成本較高。

回歸樹：

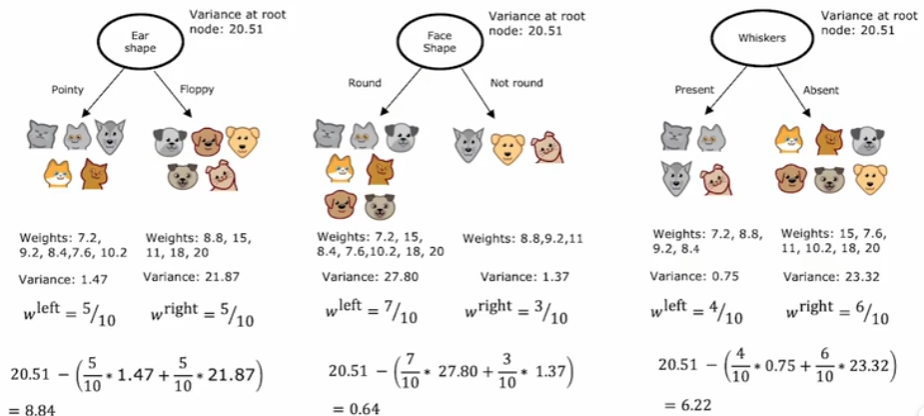
前面提到的決策樹都是解決分類問題，不過決策樹也可以推廣到解決回歸問題，也就是創建回歸樹。同樣還是上圖，此時我們不再把最右側的體重作為輸入特征，而是直接作為輸出，問題就轉變為了對于體重的預測。同樣是選取不同的輸入特征作為決策節點，現在我們要計算的不再是信息增益，之前目標是保證葉節點中的樣本更多的為一個類別，此時目標則是保證葉結點中的樣本體重盡可能接近，因為最終葉結點中所有樣本的體重均值將作為此葉結點的預測結果。所以，每一次選擇節點時，需要計算的是劃分后的方差減少量，能夠最大化降低方差的就作為當前決策節點。