目錄

一、哈希表

1.哈希算法

2.哈希碰撞

3.哈希表

4.哈希表相關操作

哈希表插入

哈希表遍歷

元素查找

哈希表銷毀

二、排序算法

1. 排序算法對比

2. 排序算法實現

冒泡排序

選擇排序

插入排序

希爾排序

快速排序

三、查找算法

1. 查找算法對比

2. 查找算法實現

順序查找

折半查找（二分查找）

一、哈希表

1.哈希算法

1. 將數據通過哈希算法映射成一個鍵值，存取都在同一個位置實現數據的高效存儲和查找，將時間復雜度盡可能降低至O(1)
2. 哈希算法是不固定的，需要選擇一個合適的哈希算法，才能映射成一個鍵值

2.哈希碰撞

多個數據通過哈希算法得到的鍵值相同，稱為產生哈希碰撞

3.哈希表

• 構建一個哈希表，存放0~100之間的數據
• 哈希算法的選擇：

將0~100之間的數據的個位作為鍵值?

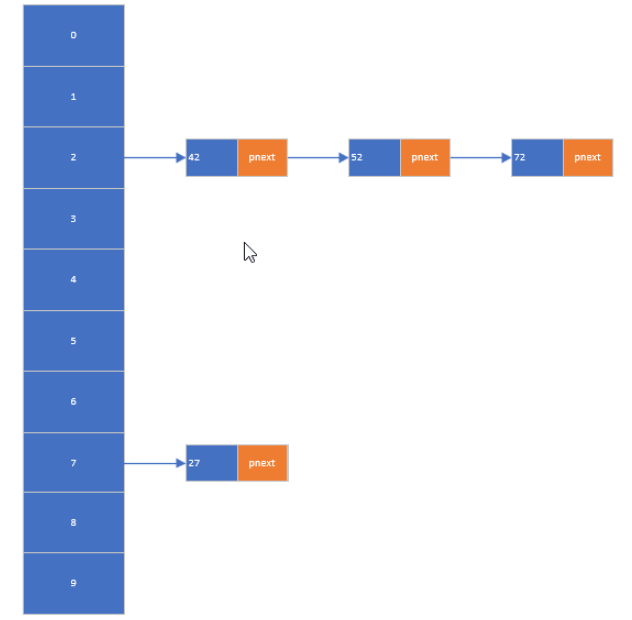
哈希表通過哈希函數實現高效存取，需解決哈希碰撞

4.哈希表相關操作

哈希表插入

#define INDEX 10  // 假設哈希表大小為10（0-9）
linknode *phashtable[INDEX] = {NULL};  // 哈希表數組/* 哈希表插入函數 */
int insert_hashtable(int tmpdata) {int key = 0;linknode **pptmpnode = NULL;  // 二級指針用于修改鏈表節點linknode *pnewnode = NULL;// 計算哈希鍵值（取數據的個位）key = tmpdata % INDEX;// 找到插入位置（保持鏈表有序）for (pptmpnode = &phashtable[key]; *pptmpnode != NULL && (*pptmpnode)->data < tmpdata; pptmpnode = &(*pptmpnode)->pnext) {// 循環移動指針至合適位置}// 申請新節點pnewnode = malloc(sizeof(linknode));if (NULL == pnewnode) {perror("fail to malloc");return -1;}// 插入新節點pnewnode->data = tmpdata;pnewnode->pnext = *pptmpnode;*pptmpnode = pnewnode;return 0;
}

哈希表遍歷

/* 遍歷哈希表所有元素 */
int show_hashtable(void) {int i = 0;linknode *ptmpnode = NULL;for (i = 0; i < INDEX; i++) {printf("%d:", i);  // 打印鍵值ptmpnode = phashtable[i];while (ptmpnode != NULL) {printf("%2d ", ptmpnode->data);  // 打印鏈表元素ptmpnode = ptmpnode->pnext;}printf("\n");}return 0;
}

元素查找

/* 查找哈希表中的元素 */
linknode *find_hashtable(int tmpdata) {int key = 0;linknode *ptmpnode = NULL;key = tmpdata % INDEX;  // 計算鍵值ptmpnode = phashtable[key];// 遍歷對應鏈表查找元素while (ptmpnode != NULL && ptmpnode->data <= tmpdata) {if (ptmpnode->data == tmpdata) {return ptmpnode;  // 找到返回節點地址}ptmpnode = ptmpnode->pnext;}return NULL;  // 未找到返回NULL
}

哈希表銷毀

/* 銷毀哈希表，釋放所有節點 */
int destroy_hashtable(void) {int i = 0;linknode *ptmpnode = NULL;linknode *pfreenode = NULL;for (i = 0; i < INDEX; i++) {ptmpnode = phashtable[i];pfreenode = phashtable[i];while (ptmpnode != NULL) {ptmpnode = ptmpnode->pnext;free(pfreenode);  // 釋放當前節點pfreenode = ptmpnode;}phashtable[i] = NULL;  // 置空數組元素}return 0;
}

二、排序算法

排序算法中，冒泡、選擇、插入排序適用于小規模數據；希爾、快速排序適用于大規模數據，其中快速排序性能最優（平均 O (nlogn)）

1. 排序算法對比

算法	時間復雜度	穩定性	核心思想
冒泡排序	O(n2)	穩定	相鄰元素比較，大元素后移，重復 n-1 次
選擇排序	O(n2)	不穩定	每次從剩余元素中找最小值，與當前位置交換
插入排序	O(n2)	穩定	將元素插入到已排序序列的合適位置，類似整理撲克牌
希爾排序	O(n^1.3)	不穩定	按步長分割數組為子序列，分別插入排序，逐步減小步長至 1
快速排序	O(nlogn)	不穩定	選基準值，將數組分為小于和大于基準的兩部分，遞歸排序兩部分

2. 排序算法實現

冒泡排序

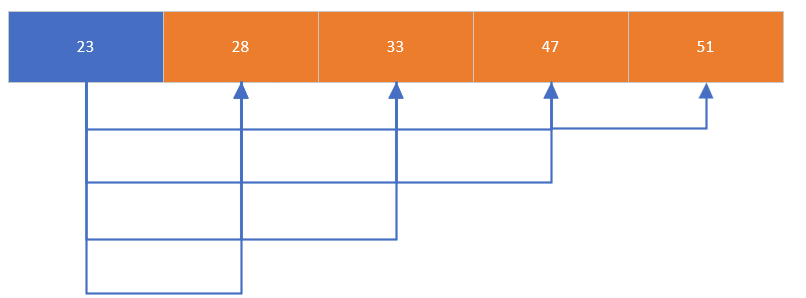
核心思想是通過相鄰元素的比較和交換，使較大的元素逐步 “浮” 到數組的末尾。具體來說，相鄰的兩個元素比較，大的向后走，小的向前走，循環找出數組中 len-1 個較大的值，最終實現整個數組的有序排列

/* 冒泡排序：相鄰元素比較交換，大元素后移 */
int bubble_sort(int *parray, int len) {int i = 0;int j = 0;int tmp = 0;for (j = 0; j < len - 1; j++) {  // 控制輪次for (i = 0; i < len - 1 - j; i++) {  // 每輪比較次數遞減if (parray[i] > parray[i + 1]) {// 交換元素tmp = parray[i];parray[i] = parray[i + 1];parray[i + 1] = tmp;}}}return 0;
}

選擇排序

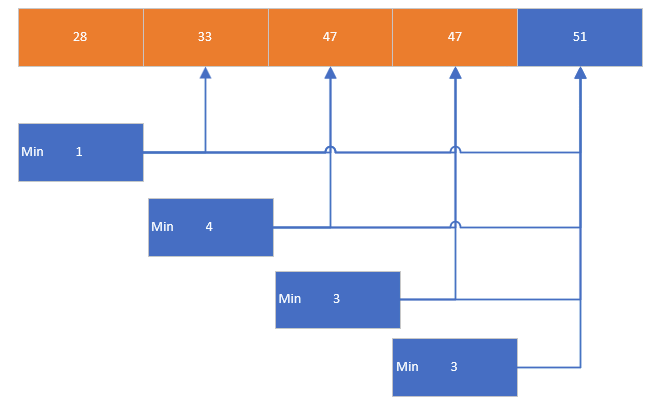
核心思想是從前到后在未排序元素中尋找最小值，然后將找到的最小值與未排序部分的前面元素進行交換。通過找到 len-1 個最小值，最后剩下的一個元素自然就是最大值，從而完成排序

/* 選擇排序：找最小值并交換到當前位置 */
int select_sort(int *parray, int len) {int i = 0;int j = 0;int tmp = 0;int min = 0;  // 最小值索引for (j = 0; j < len - 1; j++) {min = j;  // 假設當前位置為最小值for (i = j + 1; i < len; i++) {if (parray[i] < parray[min]) {min = i;  // 更新最小值索引}}// 交換最小值到當前位置if (min != j) {tmp = parray[min];parray[min] = parray[j];parray[j] = tmp;}}return 0;
}

插入排序

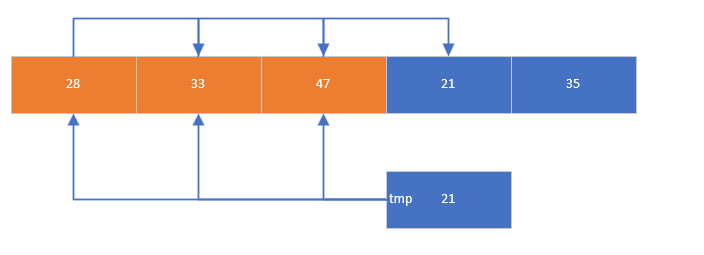
核心思想是將數組中的每個元素逐個插入到已排序的數列中。首先取出要插入的元素，然后依次和前面的元素比較，比該元素大的元素向后移動，直到遇到前一個元素比要插入的元素小，或者到達有序數列的開頭時停止，最后將該元素插入到合適位置

/* 插入排序：將元素插入已排序序列的合適位置 */
int insert_sort(int *parray, int len) {int tmp = 0;  // 待插入元素int i = 0;int j = 0;for (j = 1; j < len; j++) {tmp = parray[j];  // 取出待插入元素// 找到插入位置for (i = j; i > 0 && tmp < parray[i - 1]; i--) {parray[i] = parray[i - 1];  // 元素后移}parray[i] = tmp;  // 插入元素}return 0;
}

希爾排序

核心思想是通過選擇不同的步長，將數組拆分成若干個小的子數組，對每個子數組進行插入排序。當若干個子數組成為有序數列后，數組中的數據會大致有序，最后再對整體進行一次插入排序，以完成整個數組的排序

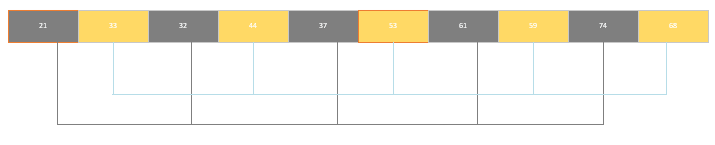
/* 希爾排序：按步長分割子序列，逐步縮小步長 */
int shell_sort(int *parray, int len) {int step = 0;  // 步長int j = 0;int i = 0;int tmp = 0;// 步長初始為len/2，每次減半至0for (step = len / 2; step > 0; step /= 2) {// 對每個子序列進行插入排序for (j = step; j < len; j++) {tmp = parray[j];for (i = j; i >= step && tmp < parray[i - step]; i -= step) {parray[i] = parray[i - step];  // 元素后移}parray[i] = tmp;  // 插入元素}}return 0;
}

快速排序

核心思想是選擇數組左邊的元素作為鍵值，從數組后面找一個比鍵值小的元素放到前面，再從前面找一個比鍵值大的元素放到后面，最后將鍵值放到中間位置。如果左右兩邊還有元素，則遞歸調用快速排序對兩邊元素進行排序

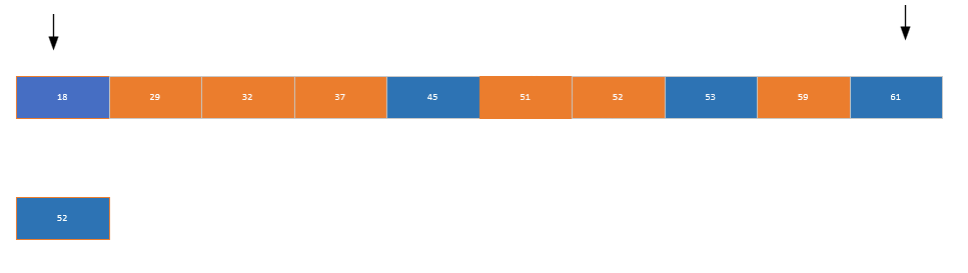
/* 快速排序：分治思想，以基準值分割數組 */
int quick_sort(int *parray, int low, int high) {int key = 0;  // 基準值int i = low;  // 左指針int j = high; // 右指針if (low >= high) {return 0;  // 遞歸終止條件}key = parray[low];  // 選最左元素為基準值while (i < j) {// 從右向左找小于基準值的元素while (i < j && parray[j] >= key) {j--;}if (i < j) {parray[i] = parray[j];  // 移至左指針位置}// 從左向右找大于基準值的元素while (i < j && parray[i] <= key) {i++;}if (i < j) {parray[j] = parray[i];  // 移至右指針位置}}parray[i] = key;  // 基準值歸位// 遞歸排序左半部分if (i - 1 > low) {quick_sort(parray, low, i - 1);}// 遞歸排序右半部分if (i + 1 < high) {quick_sort(parray, i + 1, high);}return 0;
}

三、查找算法

查找算法中，折半查找效率遠高于順序查找，但依賴有序數據

1. 查找算法對比

算法	時間復雜度	適用場景	核心思想
順序查找	O(n)	無序或小規模數據	從前往后依次遍歷，逐個比較
折半查找 （二分查找）	O(logn)	有序數組	每次取中間元素比較，縮小查找范圍至左半或右半部分

2. 查找算法實現

順序查找

從數組的起始位置開始，逐個將元素與要查找的目標值進行比較，若找到與目標值相等的元素，則查找成功；若遍歷完整個數組都沒有找到，則查找失敗

/* 順序查找：遍歷數組逐個比較 */
int seq_search(int *parray, int len, int target) {int i = 0;for (i = 0; i < len; i++) {if (parray[i] == target) {return i;  // 找到返回索引}}return -1;  // 未找到返回-1
}

折半查找（二分查找）

針對有序數組，先計算中間位置，將中間位置的元素與目標值比較。如果目標值等于中間元素，則查找成功；如果目標值大于中間元素，則在數組的右半部分繼續查找；如果目標值小于中間元素，則在數組的左半部分繼續查找，重復此過程直至找到目標值或確定查找范圍為空

/* 折半查找：僅適用于有序數組 */
int binary_search(int *parray, int low, int high, int target) {int mid = 0;if (low > high) {return -1;  // 查找失敗}mid = (low + high) / 2;  // 計算中間索引if (parray[mid] == target) {return mid;  // 找到返回索引} else if (target > parray[mid]) {// 目標在右半部分，遞歸查找return binary_search(parray, mid + 1, high, target);} else {// 目標在左半部分，遞歸查找return binary_search(parray, low, mid - 1, target);}
}