目錄
1.直接插入排序
1.1直接插入排序的思想
1.2直接插入排序的代碼邏輯:?
1.3 直接插入排序圖解?
1.4單趟排序代碼(單個元素的排序邏輯)
1.5完整排序代碼
1.6直接插入排序的時間復雜度與空間復雜度
1.7直接插入排序的優勢?
2.希爾排序(縮小增量排序)
2.1希爾排序的思想
2.2希爾排序的代碼邏輯
2.3希爾排序圖解
2.4單單趟排序代碼(對于特定的gap的一組元素的排序)
2.5單趟排序代碼(對于特定的gap的分組排序)
2.5.1一組排好序再排另一組
2.5.2 根據元素的所在組進行直接插入排序
?2.6完整排序代碼
2.6.1一組排好序再排另一組
?2.6.2 根據元素的所在組進行直接插入排序
2.7希爾排序的時間復雜度與空間復雜度
所有排序的實現皆以升序為例
1.直接插入排序
1.1直接插入排序的思想
直接插入排序的思想就是將待排序的數插入到一組有序的數中
就像打撲克牌摸牌階段,我們一張一張摸牌并整理有序的過程就是直接插入排序的過程?
1.2直接插入排序的代碼邏輯:?
創建 end 變量,初始化為有序數組中最后一個數的下標
創建 tmp變量,初始化為待排序的數值
然后將 tmp變量 與 end位置的數 從后向前 依次比較,按需要(升降序)挪動與存放數據
1.3 直接插入排序圖解?
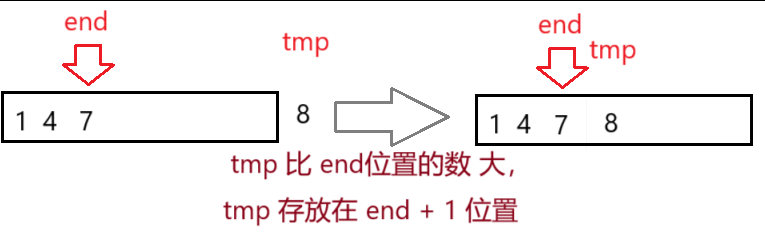
如果?tmp 比 end位置的數?大,tmp 存放在 end + 1 位置?
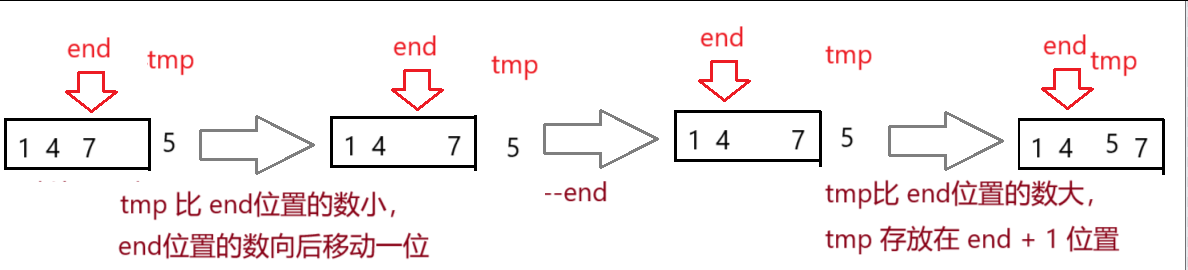
如果?tmp 比 end位置的數 小,先將end位置的數向后移動一位,再 --end
然后繼續將 tmp?與 end位置的數 從后向前 依次比較
如果?tmp 比 end位置的數?大,tmp 存放在 end + 1 位置?
(1) 依次比較,這顯然是一個循環
(2) tmp可能比所有值都小,即 end 可能 小于0 (數組下標的角度),這可以作為循環結束條件
(3) 實現正確的情況下, tmp 永遠存放在 end + 1 位置
1.4單趟排序代碼(單個元素的排序邏輯)
int end;
int tmp;
while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else break;
}
a[end + 1] = tmp;tmp 比 end位置的數 小 就一直挪動數據并--end
tmp 比 end位置的數 大 就跳出循環
因為我們知道 (實現正確下) tmp 永遠放在 end + 1 位置
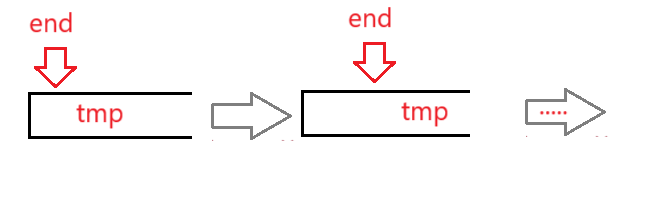
選擇在循環外面控制 tmp 存放的位置可以解決?end<0 與 end >= 0兩種情況
end >= 0,即 tmp 不存放在數組中首元素的位置

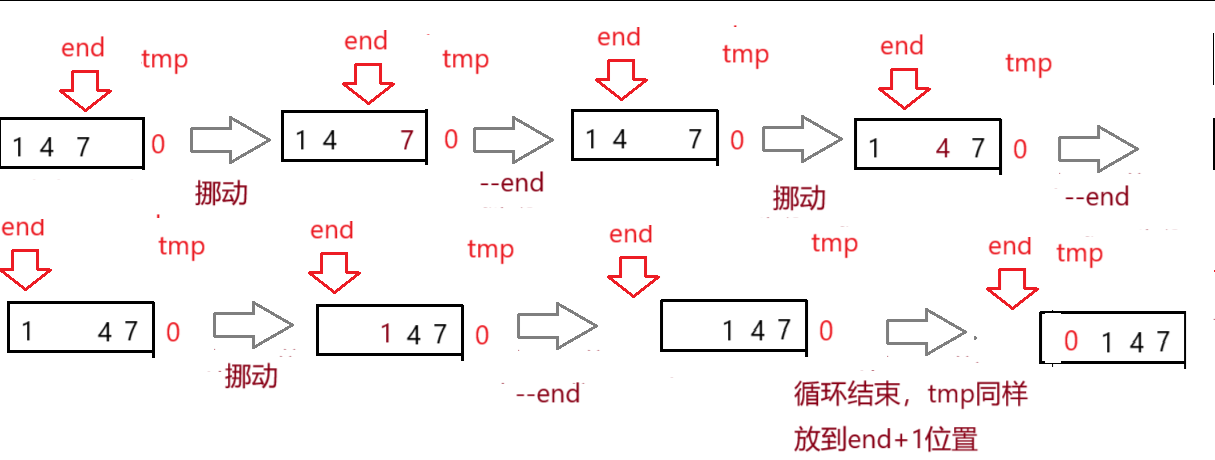
end < 0,即 tmp 比 所有數組元素都要小,不斷--end,直到循環結束,最終放在第一個位置
1.5完整排序代碼
void InsertSort(int* a, int n){ for(int i = 0; i < n - 1; ++i){int end = i;int tmp = a[i + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else break;}a[end + 1] = tmp;}
}在單趟排序的基礎上控制end與tmp即可完整代碼
一個數我們可以看作是有序的,所以 end初始值應為0,tmp初始值為數組中的第二個數
一趟比較完畢,前兩個數有序了,end位置往后挪,tmp被賦值為下一個數
這顯然也是一個循環........
1.6直接插入排序的時間復雜度與空間復雜度
直接插入排序的最壞情況就是輸入數組完全逆序,
假設數組有N個元素,即
第1次插入操作(從第2個元素(索引1)開始插入):前1個已排序元素一共后移1次
第2次插入操作:前2個已排序元素一共后移2次
第3次插入操作:前3個已排序元素一共后移3次
.........
第 N - 1 次插入操作:前N - 1 個已排序元素一共后移N - 1 次
那么移動總次數就是 ((N - 1)* N)/ 2?
所以時間復雜度就是 O(N^2)
?直接插入排序創建的變量只有i、end、tmp,變量的數量固定,所有操作均在原數組上完成
所以空間復雜度為O(1)
1.7直接插入排序的優勢?
元素集合越接近有序,直接插入排序算法的時間效率越高
2.希爾排序(縮小增量排序)
2.1希爾排序的思想
希爾排序的思想就是通過分組直接插入排序和縮小增量(gap)的操作改進普通的直接插入排序
2.2希爾排序的代碼邏輯
將間隔大小為gap(初始值一般為n/2、n/3+1)的數組元素看作一組,每組進行直接插入排序,然后縮小gap(n/2/2、(n/3+1)/3+1),再進行直接插入排序,縮小gap再排序.....
一直到gap為1的直接插入排序完成截止
顯然這是循環套循環,因為gap不斷縮小而對于每個具體的gap來說又需要進行直接插入排序
2.3希爾排序圖解
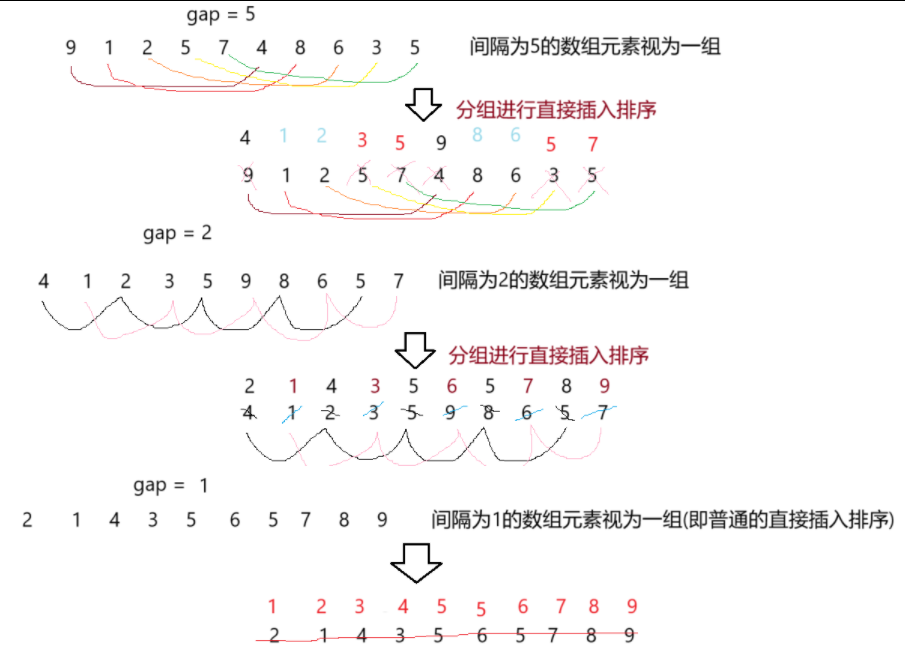
循環開始,gap初始值為n/2,直接插入排序完成后,gap /= 2,再一次直接插入排序完成后,gap/=2,此時gap縮小至1,此次直接插入排序完成后,數組有序
gap必須縮小至1,才能保證數組有序
gap也可以是 gap = gap / 3 + 1,+1是為了gap最終可縮小至1
gap /= 2不用+1 因為式子本身可以確保gap縮小至1
2.4單單趟排序代碼(對于特定的gap的一組元素的排序)
int gap;int end;int tmp;while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;}
}相對于直接插入排序,單單趟的變化簡單來說就是移動間隔從1變為了gap
2.5單趟排序代碼(對于特定的gap的分組排序)
2.5.1一組排好序再排另一組
int gap;
gap /= 2;
for(int j = 0; j < gap; ++j){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;}
}內層for循環控制的是特定的某一組數組元素的end與tmp的變化值
兩者間隔為gap,end初始值為i,tmp為其后gap個位置的值,所以i+gap<n,即i < n - gap
因為是先排好一組再排另外一組,所以需要 i+=gap
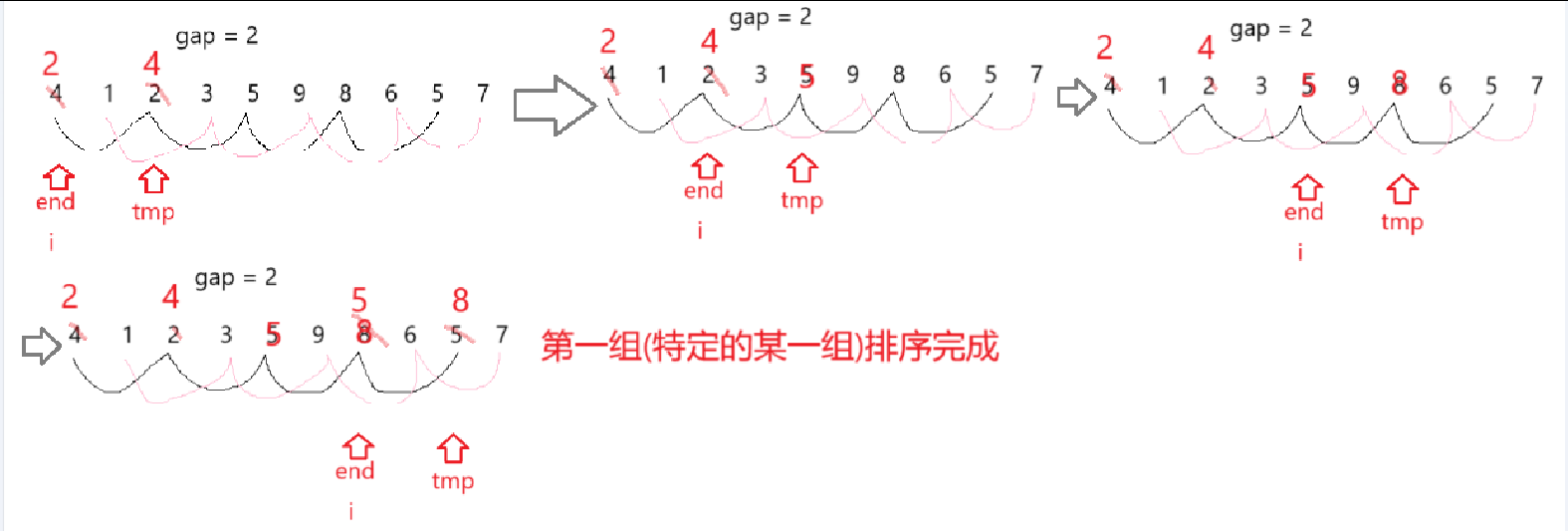
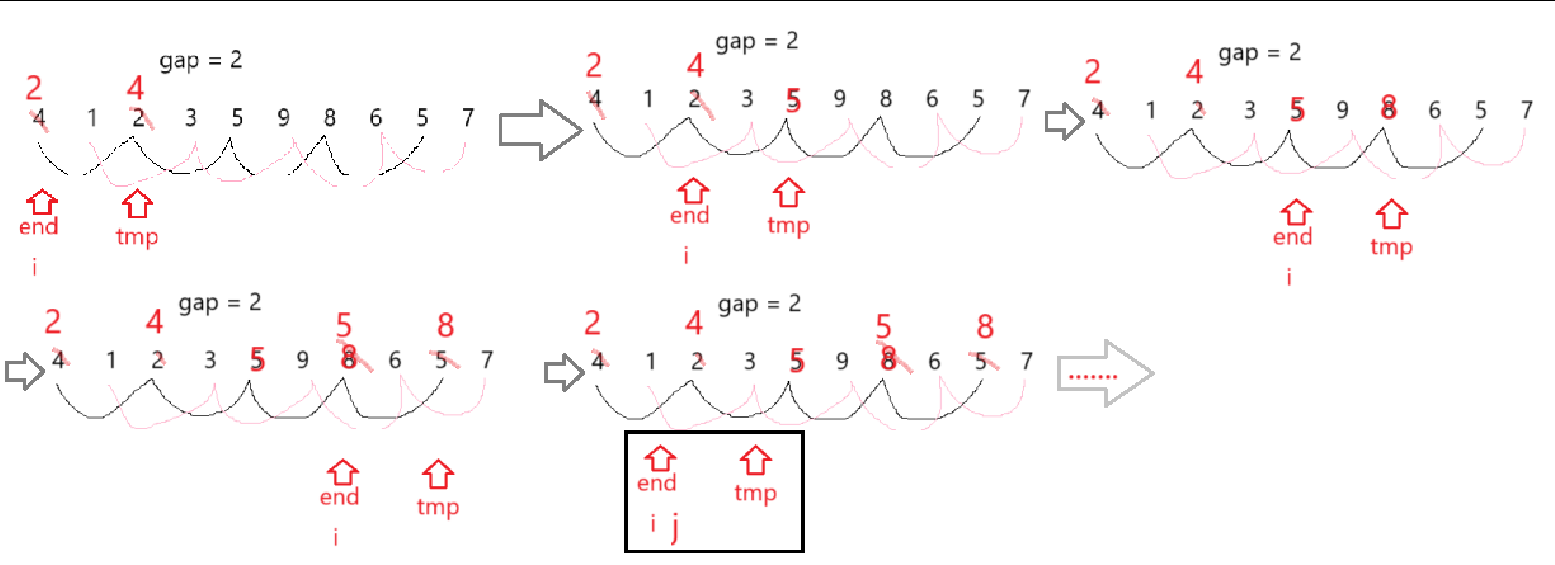
外層for循環控制的是每一組數組元素的end的初始值?
假設數組一共有n個元素,將間隔大小為gap的數組元素視為一組,那么每一組數組元素的end的初始值 一定 大于等于零小于gap(下標從零開始)
2.5.2 根據元素的所在組進行直接插入排序
int gap;
gap /= 2;
for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;
}遍歷數組元素,根據元素的所在組進行直接插入排序
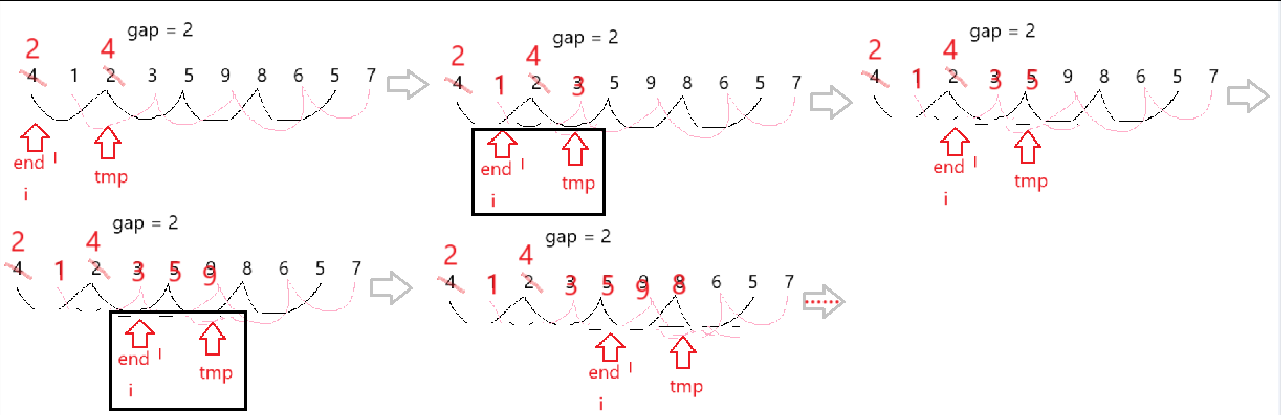
?for循環控制的是數組元素的end與tmp的變化值
兩者間隔為gap,end初始值為i,tmp為其后gap個位置的值,所以i+gap<n,即i < n - gap
通過 ++i 就可實現遍歷數組并根據元素的所在組進行直接插入排序的操作
?2.6完整排序代碼
2.6.1一組排好序再排另一組
void ShellSortUp2(int* a, int n)
{int gap = n;while (gap > 1){gap /= 2;for(int j = 0; j < gap; ++j){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}}a[end + gap] = tmp;}}}
}
通過將gap初始化為n,并將gap大于1作為循環結束條件,可以避免單個數的排序現象
再在循環內部將gap/2,也不遲
?2.6.2 根據元素的所在組進行直接插入排序
void ShellSortUp1(int* a, int n)
{int gap = n;while(gap > 1){gap /= 2;for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else break;}a[end + gap] = tmp;}}
}通過將gap初始化為n,并將gap大于1作為循環結束條件,可以避免單個數的排序現象
再在循環內部將gap/2,也不遲
2.7希爾排序的時間復雜度與空間復雜度
希爾排序的兩種實現方式本質上都是分組排序和縮小增量操作,時間復雜度沒差別
但時間復雜度完整的推導方式小編也無能為力,
只記得結論為時間復雜度為O(N*logN) ,大約是n^1.3

希爾排序的變量個數固定,所進行的操作在原數組上,所以空間復雜度為O(1)















)

)

