LeetCode 322. 零錢兌換 LeetCode 279.完全平方數 LeetCode 139.單詞拆分多重背包基礎 56. 攜帶礦石資源

LeetCode 322. 零錢兌換 ?

思路1：回溯算法可以做，只要存儲數組的最小長度即可，但可能會超時。

思路2: ? 相當于是求最大價值的相反面，另外一個物品可以使用多次，因此是個完全背包。因此這是個完全背包的求最小價值類型題目。

注意：

區分達到背包容量的方式和區分背包容量下的最大/最小價值，前者(方式)是通過累加遞推，后者(價值)是通過max和min函數來遞推。
在求最大價值時候，由于每個元素是正數，因此dp數組是初始化為0。max()函數可以有效進行覆蓋。但本題是求最小價值，因此dp數組需要初始化為float('inf')即正無窮，這樣的話min()函數可以有效進行覆蓋。另外，dp[0]是特殊情況，需要根據情況進行手動修改。

class Solution(object):def coinChange(self, coins, amount):""":type coins: List[int]:type amount: int:rtype: int"""## 每種硬幣的數量是無限的, 因此是個完全背包。## 可以湊成總金額所需的 最少的硬幣個數。關鍵在于最少的遞推公式是什么. 最少的硬幣個數不就是求最大價值的相反面嗎## 求元素的數目，與價值有關，因此背包和物品的排列順序可以任意。## 1. dp數組定義。dp[j]表示總金額（背包容量）為j下的最少硬幣個數（最少物品數量）dp = [float('inf')] * (amount + 1)      ## 求最大價值的時候，這里是初始化為0## 現在是求最小價值，這里要初始化為最大值## 2. dp初始化# dp[0] = 1       ### 不取也是一種方式。但這里不是求方式，而是求個數dp[0] = 0         ### 因此amount = 0 的時候dp[0]是0個硬幣## 3. 遞推公式# dp[j] = min(dp[j], (dp[j-coins[i]] + 1)]  ## 每進行一次加法，就證明多了一個硬幣## 4. 遍歷順序。 跟組合和排列無關，因此背包和物品的排列順序可以任意。for i in range(len(coins)):for j in range(coins[i], len(dp)):dp[j] = min(dp[j], (dp[j-coins[i]] + 1) )## 5. 打印 dpif dp[amount] == float('inf'):      ## 硬幣的種類湊不到總金額return -1return dp[amount]

LeetCode 279.完全平方數?

思路：

1. 先根據輸入的數獲取一個物品數組，這個物品長度最短為 math.sqrt(target) 。當math.sqrt(target)平方根為整數時，此時表示target可以基于math.sqrt(target)的完全平方數一次得到。若不是，則需要列出小于math.sqrt(target)的所有可能整數的完全平方數，這個數組就是物品。

2. 搞定物品后其實這道題有差不多有思路了，另外的，遞推公式記得+1，因為是要求數量，沒加1的話就變成了求構成的完全平方數中的最小元素。

Code:

import math
class Solution(object):def numSquares(self, n):""":type n: int:rtype: int"""### 最少數量即最小價值，物品背包遍歷先后順序不影響### 由于第一個物品可以被用多次，因此是完全背包類型### 物品是一個正整數組 [1,2,3,...,n]### 將上述正整數組平方得到一個正整數組的平方數組[2,4,9,...,n^2]### 最大背包容量為nnums = [0]* (int(math.sqrt(n)))for i in range(len(nums)):nums[i] = (i+1)*(i+1)       ### 起始坐標是從0開始，要右移一位# 1. dp 定義，dp[j]，整數為j下，和為j的完全平方數的最少數量dp = [float('inf')] * (n+1)# 2. dp 初始化    dp[0] = 0   ## 0 本身可以不通過別人平方相加得到# 3. 遞推公式# dp[j] = min(dp[j], dp[j-nums[i]])# dp[j] = min(dp[j], dp[j-nums[i]]+1)   ## 衡量的是數量因此要加1，而不是上述這個，這個是求其中的一個最小元素。# 4. 遍歷順序for i in range(len(nums)):              # 先遍歷物品for j in range(nums[i], len(dp)):   # 再遍歷背包dp[j] = min(dp[j], dp[j-nums[i]]+1)# 5. 打印dp# print(dp)return dp[n]

LeetCode?139.單詞拆分

類似題目：

LeetCode 131: 分割回文串。這道題是字符串拆分成回文串，而本題是判斷字典中的單詞能否組成字符串。

思路：

這道題偏難，即考究字符串的操作，又考究了雙指針，結合雙指針來設計dp數組。通過一個雙指針來遍歷指針之間的子字符串是否存在于字典中來進行判斷，并將判斷結果更新到dp數組中。如下所示：

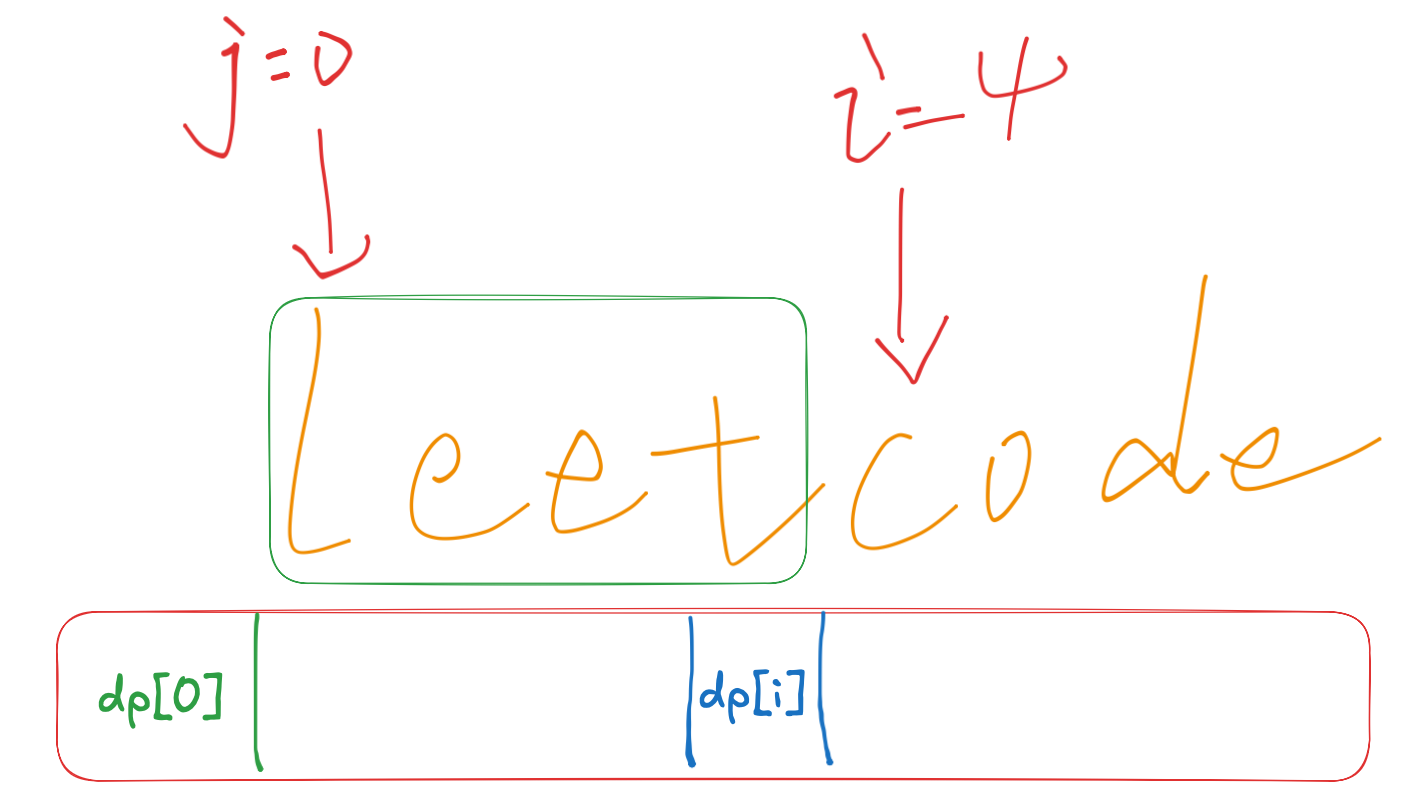
根據字符串的關系去更新dp數組是關鍵，下標多會有點亂，要理清dp的下標含義和i,j指向字符串時又表達什么意思。遞推公式那里要搞懂。

確定遞推公式

如果確定dp[j] 是true，且 [j, i] 這個區間的子串出現在字典里，那么dp[i]一定是true。（j < i ）。

所以遞推公式是 if([j, i] 這個區間的子串出現在字典里 && dp[j]是true) 那么 dp[i] = true。

Code

class Solution(object):def wordBreak(self, s, wordDict):""":type s: str:type wordDict: List[str]:rtype: bool"""### 物品可以被多次使用，因此是完全背包。### 在數字數組中，求和問題可以通過相加來判斷。關鍵：但在字符串中，如何判斷字典中的單詞拼接起來能否構成該target字符串# 1. dp數組定義。dp[j]表示長度為j的字符串能否由單詞表中的單詞構成。dp = [False] * (len(s) + 1)     # 2. dp數組初始化。先默認不能由單詞表中的單詞構成。dp[0] = True            ## 第一個表示空字符串## 雖題目默認了不會有空字符串，但dp[0]需要初始化為True，如果初始化為False, 則后面無法進行遞推，所得到的都會是False# 3. 遞推公式。關鍵：遞推公式是什么？# if dp[j] == True and [j,i] in word_dict:     ## 如果字符串中的前i個已匹配，且[i，j]這個位置存在子字符串。#       dp[i] = True# 4. 遍歷順序。單詞的構成涉及到排列，因此是先遍歷背包再遍歷物品。for i in range(1, len(dp)):    ## 先遍歷背包for j in range(i):         ## 再遍歷物品, j始終都是在i的左邊，j去追趕i, j和i的這段距離內的子字符串sub_string = s[j:i]    ## j位置開始(包括j)到i(不包括i)的這段子字符串。 i-j這段區間有i-j個字符if dp[j] == True and sub_string in wordDict:dp[i] = True       ## j + i - j = i，前j個字符可行，現在從第j開始的i-j個字符可行，因此前i個字符可行# break             ## 不break也可以，break是對一些多余的循環進行剪枝# 5. 打印dp數組return dp[len(s)]

多重背包基礎

01背包是一個物品只能用一次
完全背包是一個物品能用無數次
多重背包是一個物品能用x次

涉及多重背包的題目較少，如遇到的話，將其轉化為01背包就行。如下所示：

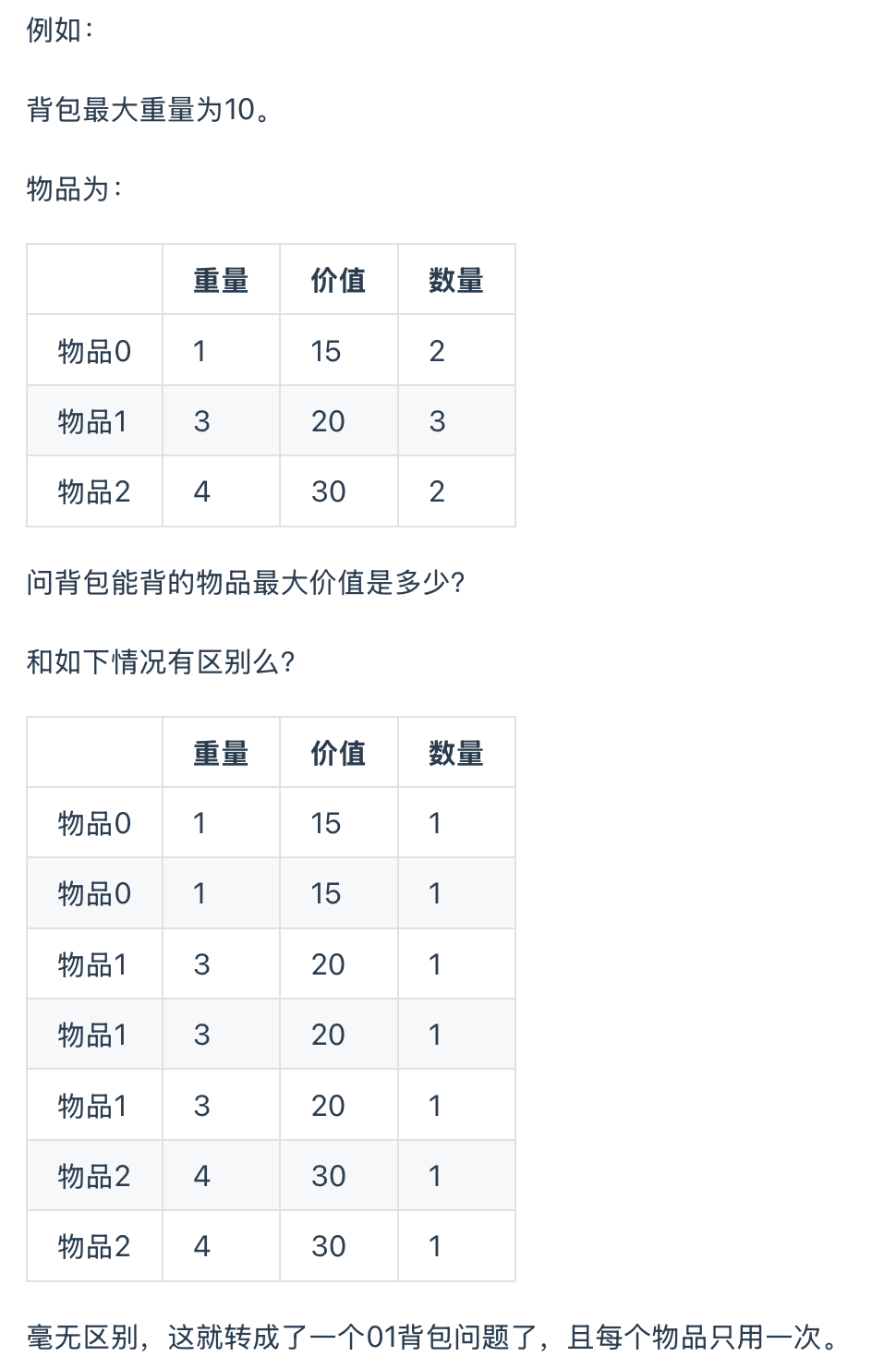
56. 攜帶礦石資源

思路1：

將多重背包轉換為01背包進行解決。

需要注意如何將多重轉換為01問題，另外01問題在遍歷背包時需要注意順序。

Code

bagroom, category = input().split()
bagroom, category = int(bagroom), int(category)weight = []
for x in input().split():weight.append(int(x))price = []
for x in input().split():price.append(int(x))nums = []
for x in input().split():nums.append(int(x))for i in range(len(nums)):      ### 將多重背包轉換為01背包處理, 但如果nums數目過大的話，會導致01背包中物品數組的長度很大，進而導致超時。count = nums[i]while count != 1:weight.append(weight[i])price.append(price[i])count -= 1# 1. dp定義，dp[j]表示背包容量為j下背包的最大價值
dp = [0] * (bagroom + 1)# 2. dp初始化，初始化為0
# 3. 遞推公式。dp[j] = max(dp[j], dp[j-weight[i]+price[i]])
# 4. 遍歷順序
for i in range(len(weight)):                ## 先物品再背包容量for j in range(len(dp)-1, weight[i]-1, -1): ## 01背包這里要逆序遍歷，確保每個物品只用一次dp[j] = max(dp[j], dp[j-weight[i]]+price[i])
# 5. 打印dp數組
# print(dp)
print(dp[bagroom])

思路2：

對物品的數目也進行一個循環操作，來判斷物品的數目添加多少時可以達到最大價值。其實就是多加了個循環來判斷當前物品要裝多少個，來得到最大價值。

Code:

bagroom, category = input().split()
bagroom, category = int(bagroom), int(category)weight = []
for x in input().split():weight.append(int(x))price = []
for x in input().split():price.append(int(x))nums = []
for x in input().split():nums.append(int(x))# 1. dp定義，dp[j]表示背包容量為j下背包的最大價值
dp = [0] * (bagroom + 1)# 2. dp初始化，初始化為0
# 3. 遞推公式。dp[j] = max(dp[j], dp[j-k*weight[i]+k*price[i]])
# 4. 遍歷順序
for i in range(len(weight)):                ## 先物品再背包容量for j in range(len(dp)-1, weight[i]-1, -1): ## 這里要逆序遍歷，確保每個物品只用一次for k in range(1, nums[i]+1):   ## nums[i]+1 確保最后一個數可以被遍歷到。range是左閉右開。if j < k*weight[i]:     ## 背包容量不夠，那再大的k可以不用遍歷了breakdp[j] = max(dp[j], dp[j-k*weight[i]]+ k*price[i])# 5. 打印dp數組
# print(dp)
print(dp[bagroom])