1. 線性回歸模型

1.1 線性回歸模型

線性回歸模型：將數據擬合成一條直線。

作用：預測數字作為輸出。

例子：

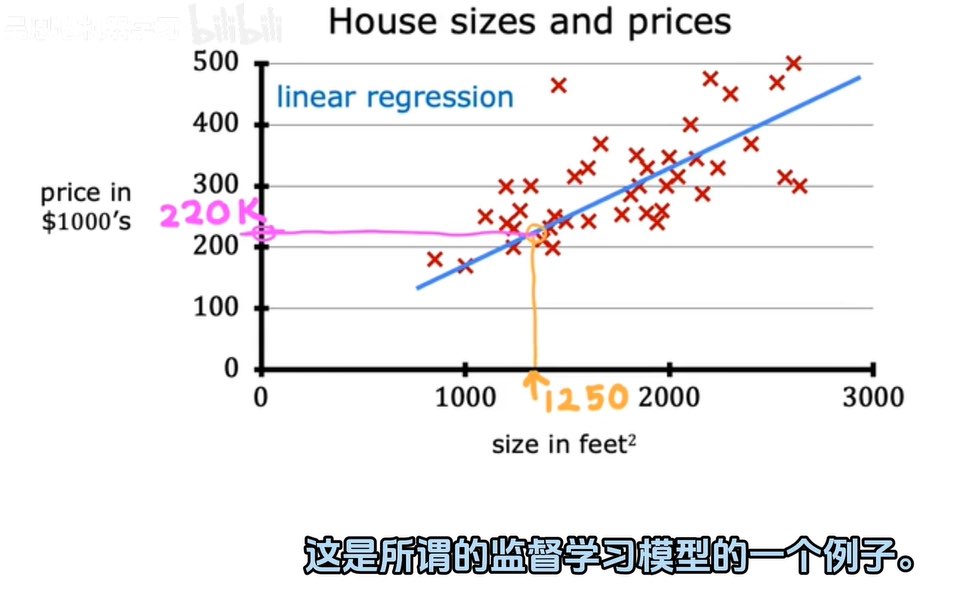
房子的大小與房價的估計

（圖表）

（數據表）

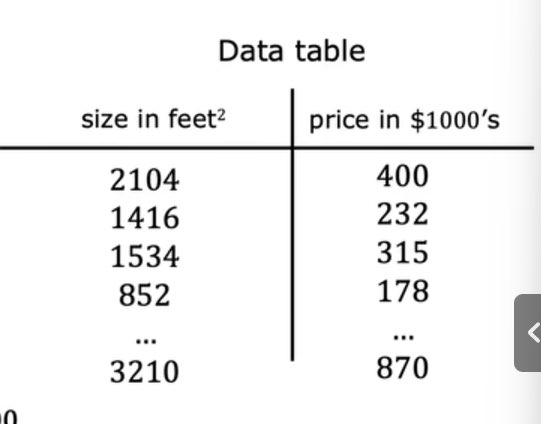
1.2 訓練集

訓練集：用于訓練模型的數據集

訓練集作業例子：要預測客戶的房價，首先要訓練模型以從訓練集中學習，然后該模型可以預測客戶的房價。

輸入的標準符號：x（輸入變量/特征/輸入特征）

預測的輸出變量的標準符號：y（目標變量）

單個訓練示例：（x，y）

引用一個具體的訓練例子：

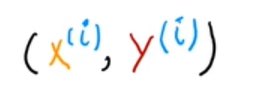
i表示第幾個訓練示例。

1.3?監督學習的工作工作過程

要訓練模型，需要將訓練集（包括輸入特征和輸出目標）提供給學習算法。然后監督學習算法會產生一些功能（函數f）。

函數f：輸入x，輸出預測y值。

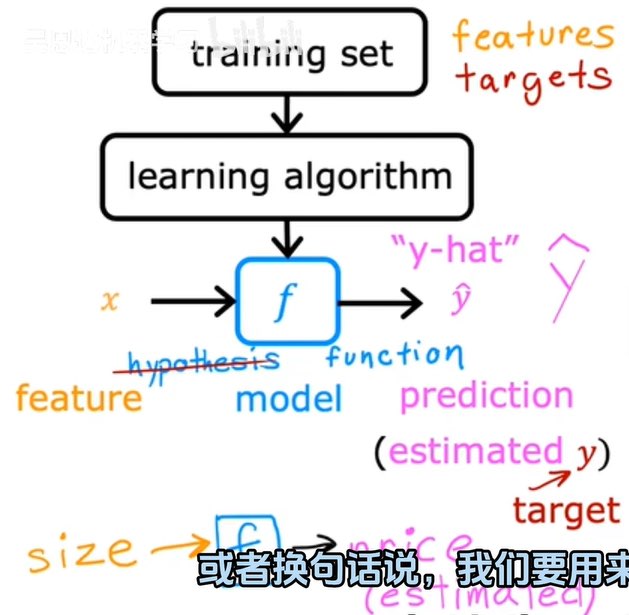
如何表示函數f：

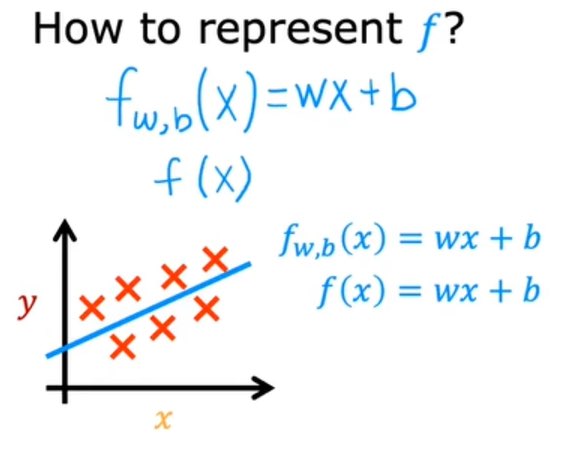
上面的直線即單線性回歸模型。

1.4 代價函數/成本函數

代價函數：表示一個用于衡量模型預測值與真實值之間差異的函數，目標是通過最小化這個函數來優化模型參數。

成本函數（平方誤差成本函數）：

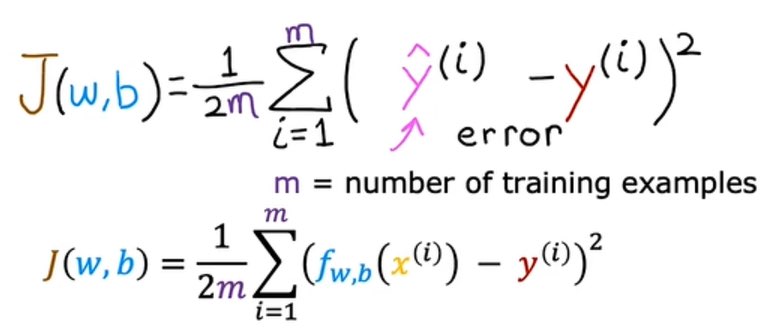
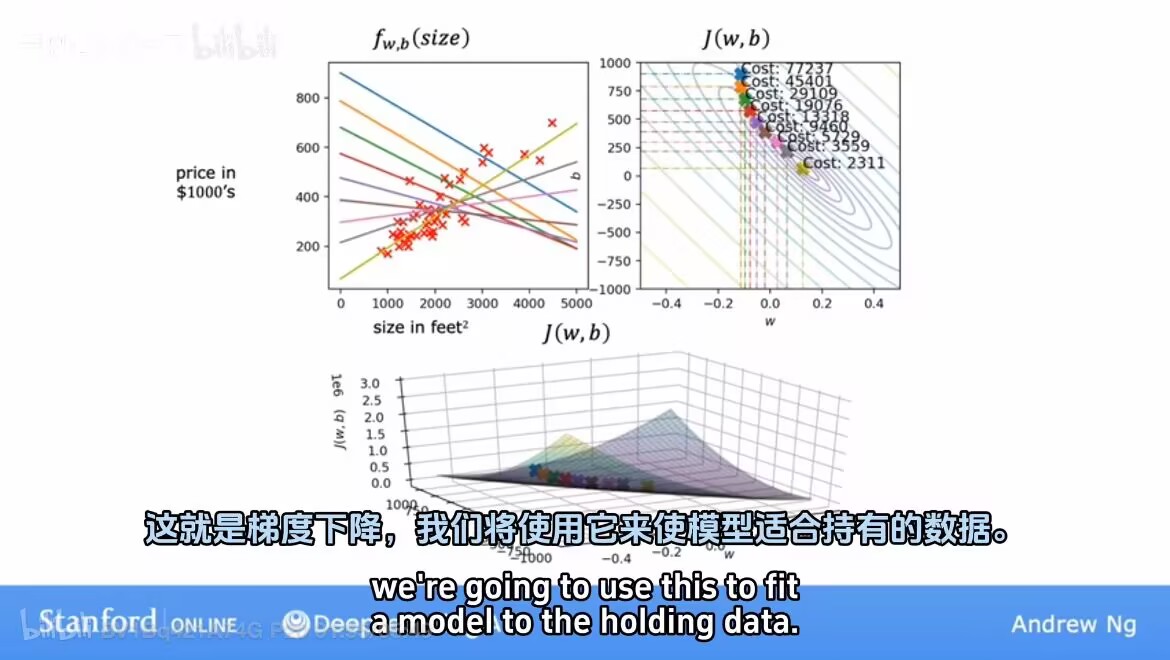
成本函數在三個維度：

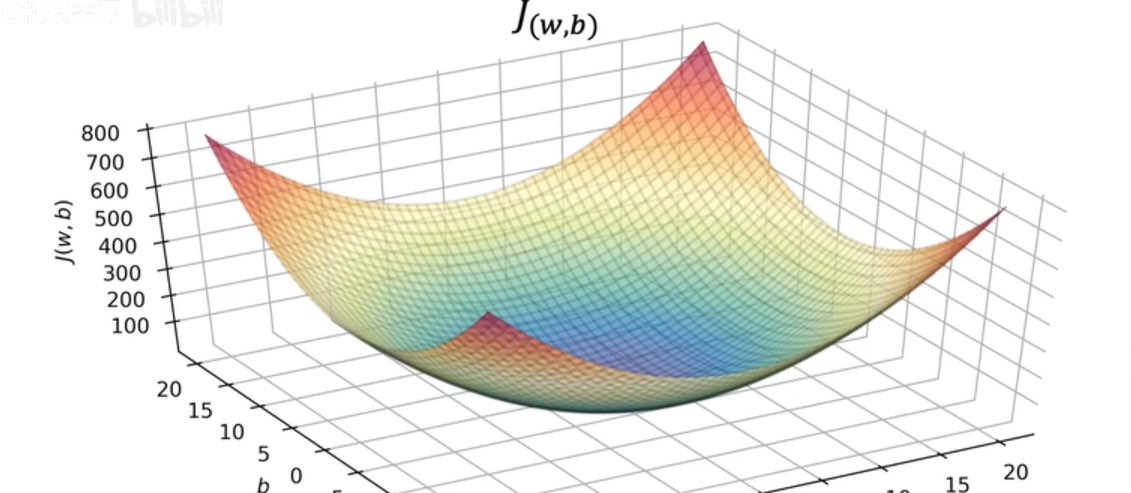
如何實現最小化成本函數---梯度算法。

2. 梯度算法

2.1?梯度算法

梯度算法：每次稍微改變參數w和b以嘗試降低w和b的成本j，知道希望j穩定最小值或者接近最小值。對于某些可能不是弓形或者吊床形的函數j，可能存在不止一個最小值。

2.2 實現梯度下降

梯度下降算法：

a：學習率，取值0~1，控制下坡步幅。

導數：成本函數j的導數項，控制往哪個方向邁步。

2.3 梯度下降的直觀理解

上面解釋了w會正確移向最低點。

2.4 學習率

a太小時：梯度下降會起作用，但是下降的速度太慢。

a太大時：梯度下降可能會超過，并且可能永遠不會達到。（梯度下降可能無法達到收斂，甚至可能發散）

當更新時候w不變，表示參數已經使得j達到局部最小值。

當接近局部最小梯度下降時，會自動采取更小的步長。（因為斜率在變小）

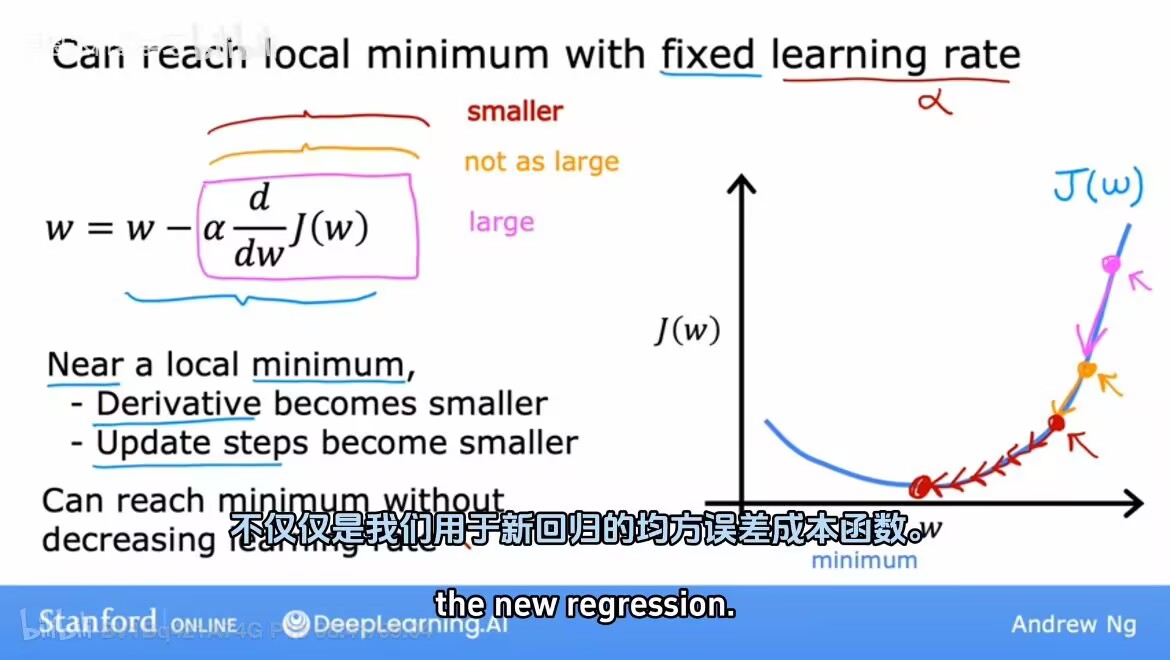
2.5 線性回歸中的梯度下降

重復執行上面式子知道收斂為止。

運行梯度下降：