引言

前序學習進程中，已經學習了超平面的基礎知識，學習鏈接為：超平面
在此基礎上，要想正確繪制超平面，還需要了解感知機的相關概念。

感知機

感知機是對生物神經網絡的模擬，當輸入信號達到感知機的閾值時，會輸出感應信號，否則不會有任何反應。
這里先對感知機建立數學模型。
對于向量F和向量G，有：
$$\bar{F}=(f0,f1,f2,...,fn),\bar{G}=(g0,g1,g2,...,gn)$$定義向量點積：$$H=\bar{F}?\bar{G}$$

如果滿足：
$$H=\{\begin{array}{c}1\text{if?}H\ge 0\\ ?1\text{if?}H<0\end{array}$$
相應的，在numpy模塊中，也有一個sign()函數可以對感知機的數學模型進行精煉表達，這有一個代碼實例：

# 引入numpy模塊
import numpy as np
# 引入數據
x=[1,2,3,-6,-8,-10]
# np.sign()函數測試
z=np.sign(x)
print('z=',z)

代碼運行后的輸出效果為：

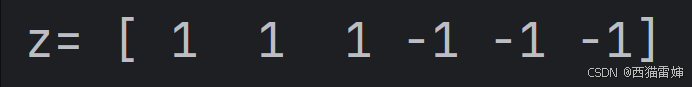
非常明顯，對于非負數，np.sign()函數輸出1，對于負數則直接輸出0。

一個關于感知機的項目

這里有一個感知機算法的簡單項目：

# 引入模塊
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from matplotlib.colors import ListedColormap# 定義隨機數種子
# 定義了隨機數種子后，每次產生的隨機數是一樣的
# 使用不同的隨機數種子，會得到不同的初始隨機數
np.random.seed(88)def perceptron_learning_algorithm(x, y):# W是3個在[0,1)區間上均勻分布的隨機數w = np.random.rand(3)# misclassified_examples是由predict()函數計算獲得misclassified_examples = predict(hypothesis, x, y, w)while misclassified_examples.any():x_example, expect_y = pick_one_from(misclassified_examples, x, y)# 更新權重w = w + x_example * expect_y# 重新代入predict()函數進行評估misclassified_examples = predict(hypothesis, x, y, w)return w# hypothesis函數對w和x兩個向量的點積進行感知機運算
# hypothesis函數返回值是1或者-1
def hypothesis(x, w):return np.sign(np.dot(w, x))# predict函數包括4個變量
def predict(hypothesis_function, x, y, w):# np.apply_along_axis函數先將x按照行取出，這是由axis=1決定的取值方式# hypothesis_function每次接收x的一行和wpredictions = np.apply_along_axis(hypothesis_function, 1, x, w)# y != predictions表示分類錯誤，這個！代表的不等于判斷會輸出布爾結果False和True# x[y != predictions]直接輸出x[y != predictions]取值為True時對應x行的數據misclassified = x[y != predictions]return misclassified# pick_one_from函數
def pick_one_from(misclassified_examples, x, y):# 隨機打亂分類樣本的順序np.random.shuffle(misclassified_examples)t = misclassified_examples[0]index = np.where(np.all(x == t, axis=1))[0][0]return x[index], y[index]# 使用sklearn生成線性可分的數據集
x, y = make_classification(n_samples=100,n_features=2,n_redundant=0,n_informative=2,n_clusters_per_class=1,random_state=42,class_sep=2.0
)# 將標簽從0/1轉換為-1/1
y = np.where(y == 0, -1, 1)# 添加偏置項
x_augmented = np.c_[np.ones(x.shape[0]), x]# 訓練感知機模型
w = perceptron_learning_algorithm(x_augmented, y)
print("感知機權重:", w)# 繪制分類效果圖
plt.figure(figsize=(10, 8))# 繪制數據點
plt.scatter(x[y==1][:, 0], x[y==1][:, 1], c='blue', marker='o', label='Class +1', edgecolor='k', s=70)
plt.scatter(x[y==-1][:, 0], x[y==-1][:, 1], c='red', marker='o', label='Class -1', s=70)# 繪制決策邊界
x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),np.arange(y_min, y_max, 0.02))# 預測網格點的分類
Z = np.array([hypothesis(np.array([1, a, b]), w) for a, b in zip(xx.ravel(), yy.ravel())])
Z = Z.reshape(xx.shape)# 繪制分類區域
cmap_light = ListedColormap(['#FFAAAA', '#AAAAFF'])
plt.contourf(xx, yy, Z, cmap=cmap_light, alpha=0.3)# 繪制決策邊界
plt.contour(xx, yy, Z, levels=[0], linewidths=2, colors='black')# 添加圖例和標題
plt.title('Perceptron Classification Results', fontsize=16)
plt.xlabel('Feature 1', fontsize=14)
plt.ylabel('Feature 2', fontsize=14)
plt.legend(loc='upper right', fontsize=12)
plt.grid(True, linestyle='--', alpha=0.7)
plt.tight_layout()plt.show()

代碼運行后，會獲得直接的分類效果：

下一件文章將詳細解讀代碼。

總結

學習了感知機的基本概念。