有效的數據準備對于構建強大的機器學習模型至關重要。本文檔總結并闡述了為監督和非監督學習任務準備數據的關鍵技術。
1. 理解數據類型
有兩種數據類型。定性數據描述對象的特征,而定量數據描述對象的數量。
定性(分類)數據
- 名義:無序的命名類別(例如,性別,國家)。
- 無法執行算術運算。
- 使用獨熱編碼或標簽編碼。
- 有序:具有自然順序的類別(例如,滿意度:低,中,高)。
- 通常用整數映射編碼,保留順序。
定量(數值)數據
- 區間:具有有意義差異的數值數據,但無真實零點(例如,攝氏溫度)。
- 可以計算均值、中位數、標準差。
- 比率:具有真實零點的數值數據(例如,收入,年齡)。
- 所有算術運算有效。
離散與連續屬性
- 離散:可計數的值(例如,子女數量)。
- 連續:范圍內無限值(例如,身高,體重)。
2. 探索與總結數據
一旦從現實世界獲取數據(數據收集),我們需要探索和總結數據(數據分析)。在這個階段通常使用可視化來理解數據分布(數據分散度量)。
中心趨勢度量
- 均值:對異常值敏感。
- 中位數:對異常值魯棒,適用于偏態數據。
- 眾數:出現頻率最高的值。
分布度量
- 方差與標準差:顯示數據如何圍繞均值分布。
- 范圍、四分位數、四分位距:幫助檢測異常值和數據偏態。
3. 數據可視化
可視化數據有很多方法。以下是一些常見的方法。
在示例中,我們將使用 matplotlib 庫來繪制它們。
箱線圖
- 可視化五數概括:最小值,Q1,中位數,Q3,最大值。
- 突出顯示超出 1.5 × 四分位距的異常值。
直方圖
- 顯示頻率分布。
- 幫助識別偏態、模態和分布范圍。
散點圖
- 用于雙變量關系。
- 揭示兩個變量之間的相關性和模式。
交叉表
- 用于探索分類變量之間的關系。
- 在矩陣中顯示頻率分布。
4. 數據質量問題與修復
處理缺失值和異常值是數據準備的重要步驟。現實世界的數據往往不完美。缺失數據、異常值和其他問題需要在此步驟中解決,以實現有效的機器學習。
缺失值
- 原因:調查未響應、手動輸入錯誤、數據損壞。
- 修復方法:
- 刪除:移除缺失數據的行/列(僅在安全的情況下)。
- 插補:
- 均值/中位數(數值)
- 眾數(分類)
- 基于組的插補(例如,按相似行)
- 基于模型的估計:使用預測建模或相似性函數。
刪除通常在刪除一些數據行不會損失太多信息時應用。這通常與 dropna() 方法相關。另一方面,插補可能是一種更實際的方法,通過為缺失數據提供人工值來保留重要數據屬性,同時不影響數據分布。
什么是插補?
插補是用替代值替換缺失數據的過程。這很關鍵,因為大多數機器學習算法無法直接處理缺失值。
常見的插補方法:
- 均值/中位數插補:用列的均值或中位數替換缺失值。
- 適用于:無異常值的正態分布數據
- 使用場景:數據完全隨機缺失時
- 基于組的插補:用組的均值/中位數替換缺失值
- 適用于:數據有意義的組
- 示例:根據汽車氣缸數填充缺失的馬力
- KNN插補:使用k近鄰插補缺失值
- 適用于:數據存在模式
- 最準確但計算成本高
- 任意值插補:用-999等值替換
- 適用于:基于樹的模型
- 使用場景:希望缺失值突出時
異常值
異常值是與其他觀測值顯著不同的數據點。可能由測量錯誤、數據輸入錯誤或自然變異引起。
異常值的影響:
- 可能使統計度量偏斜
- 可能影響模型性能
- 可能導致模型受極端值影響過大
檢測方法:
- 四分位距方法:
- 計算Q1(25th百分位)和Q3(75th百分位)
- 四分位距 = Q3 - Q1
- 下限 = Q1 - 1.5*四分位距
- 上限 = Q3 + 1.5*四分位距
- 超出這些界限的點被視為異常值
- Z分數方法:
- 計算Z分數:z = (x - 均值) / 標準差
- |z| > 3 的點通常被視為異常值
處理技術:
- 封頂(Winsorization):將異常值替換為最近的非異常值
- 轉換:應用對數、平方根或其他轉換
- 移除:如果異常值是錯誤或不具代表性
- 單獨建模:為異常值創建單獨的模型
5. 特征縮放
許多機器學習算法在特征具有相似尺度時表現更好或收斂更快。縮放還確保不同量級的特征不會主導模型學習。
標準化(Z分數)
x ′ = x ? μ σ x' = \frac{x - \mu}{\sigma} x′=σx?μ?
- 將數據中心化到均值為0,單位方差。
- 用于數據有異常值或正態分布時。
歸一化(最小-最大縮放)
x ′ = x ? x min x max ? x min x' = \frac{x - x_{\text{min}}}{x_{\text{max}} - x_{\text{min}}} x′=xmax??xmin?x?xmin??
- 將特征縮放到[0, 1]范圍。
- 對異常值敏感。
魯棒縮放
- 使用中位數和四分位距
- 公式:(x - 中位數) / 四分位距
- 適用于:有異常值的數據
何時縮放?
- 需要縮放的場景:
- 基于距離的算法(KNN、K均值、帶RBF核的SVM)
- 神經網絡
- 正則化模型(Ridge、Lasso)
- 主成分分析(PCA)
- 無需縮放的場景:
- 基于樹的模型(決策樹、隨機森林、XGBoost)
- 樸素貝葉斯
6. 降維
減少特征數量,同時保留重要信息。
為什么降維?
- 維度災難:隨著維度增加,數據變得稀疏
- 減少過擬合:更少的特征意味著更少的參數需要學習
- 加速訓練:減少計算需求
- 改進可視化:更容易可視化2D或3D數據
主成分分析(PCA)
- 將數據投影到最大化方差的主成分上
- 步驟:
- 標準化數據
- 計算協方差矩陣
- 計算特征向量和特征值
- 選擇前k個特征向量
- 將數據轉換到新空間
何時使用:
- 當特征相關時
- 用于可視化
- 在訓練具有許多特征的模型之前
- 用于噪聲減少
奇異值分解(SVD)
- 矩陣分解方法,用于識別潛在特征。
7. 特征選擇
選擇最相關的特征子集以:
- 減少過擬合
- 提高模型可解釋性
- 降低計算成本
特征類型:
- 無關:無預測能力。
- 冗余:與其他特征重復信息。
方法:
- 過濾方法:
- 根據統計測試選擇特征
- 示例:相關系數、卡方檢驗
- 快速但不考慮特征交互
- 包裝方法:
- 使用特征子集訓練模型
- 示例:遞歸特征消除(RFE)
- 計算成本高但更準確
- 嵌入方法:
- 特征選擇作為模型訓練的一部分
- 示例:Lasso回歸、決策樹
- 高效且準確,但特定于模型
總結表
| 任務 | 技術 |
|---|---|
| 識別變量類型 | 名義、有序、區間、比率 |
| 總結數值數據 | 均值、中位數、標準差、四分位距 |
| 可視化數據 | 直方圖、箱線圖、散點圖 |
| 處理缺失值 | 刪除、插補、預測 |
| 處理異常值 | 移除、封頂、調查 |
| 縮放特征 | 標準化、歸一化 |
| 降維 | 主成分分析、奇異值分解 |
| 選擇特征 | 過濾、包裝、嵌入方法 |
此筆記本使用關于汽車屬性和燃油效率的假數據集說明數據準備的關鍵技術點。
示例數據集
# 導入所需庫
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler
from sklearn.impute import SimpleImputer, KNNImputer
from sklearn.decomposition import PCA
from sklearn.feature_selection import SelectKBest, f_regression, RFE
from sklearn.linear_model import LinearRegression# 假數據集
data = {"car_name": ["car_a", "car_b", "car_c", "car_d", "car_e", "car_f"],"cylinders": [4, 6, 8, 4, 4, 8],"displacement": [140, 200, 360, 150, 130, 3700],"horsepower": [90, 105, 215, 92, np.nan, 220], # np (numpy - 數字Python - 用于科學計算的庫。nan: 非數字/空值)"weight": [2400, 3000, 4300, 2500, 2200, 4400],"acceleration": [15.5, 14.0, 12.5, 16.0, 15.0, 11.0],"model_year": [80, 78, 76, 82, 81, 77],"origin": [1, 1, 1, 2, 3, 1],"mpg": [30.5, 24.0, 13.0, 29.5, 32.0, 10.0]
}
df = pd.DataFrame(data)
df
| car_name | cylinders | displacement | horsepower | weight | acceleration | model_year | origin | mpg | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | car_a | 4 | 140 | 90.0 | 2400 | 15.5 | 80 | 1 | 30.5 |
| 1 | car_b | 6 | 200 | 105.0 | 3000 | 14.0 | 78 | 1 | 24.0 |
| 2 | car_c | 8 | 360 | 215.0 | 4300 | 12.5 | 76 | 1 | 13.0 |
| 3 | car_d | 4 | 150 | 92.0 | 2500 | 16.0 | 82 | 2 | 29.5 |
| 4 | car_e | 4 | 130 | NaN | 2200 | 15.0 | 81 | 3 | 32.0 |
| 5 | car_f | 8 | 3700 | 220.0 | 4400 | 11.0 | 77 | 1 | 10.0 |
數據類型
car_name:名義(分類)cylinders,origin:有序/分類displacement,horsepower,weight,acceleration,mpg:比率(數值)model_year:區間
處理缺失值
# 1. 處理缺失值示例
print("=== 插補前的缺失值 ===")
print(df.isna().sum())# 均值插補
mean_imputer = SimpleImputer(strategy='mean')
df['horsepower_mean'] = mean_imputer.fit_transform(df[['horsepower']])# 基于組的插補
group_means = df.groupby('cylinders')['horsepower'].transform('mean')
df['horsepower_group'] = df['horsepower'].fillna(group_means)# KNN插補
knn_imputer = KNNImputer(n_neighbors=2)
df['horsepower_knn'] = knn_imputer.fit_transform(df[['horsepower']])print("\n=== 插補后 ===")
df[['horsepower', 'horsepower_mean', 'horsepower_group', 'horsepower_knn']]
=== 插補前的缺失值 ===
car_name 0
cylinders 0
displacement 0
horsepower 1
weight 0
acceleration 0
model_year 0
origin 0
mpg 0
dtype: int64=== 插補后 ===
| horsepower | horsepower_mean | horsepower_group | horsepower_knn | |
|---|---|---|---|---|
| 0 | 90.0 | 90.0 | 90.0 | 90.0 |
| 1 | 105.0 | 105.0 | 105.0 | 105.0 |
| 2 | 215.0 | 215.0 | 215.0 | 215.0 |
| 3 | 92.0 | 92.0 | 92.0 | 92.0 |
| 4 | NaN | 144.4 | 91.0 | 144.4 |
| 5 | 220.0 | 220.0 | 220.0 | 220.0 |
處理異常值
# 2. 處理異常值示例
def detect_and_handle_outliers(df, column):# 計算四分位距Q1 = df[column].quantile(0.25)Q3 = df[column].quantile(0.75)IQR = Q3 - Q1lower_bound = Q1 - 1.5 * IQRupper_bound = Q3 + 1.5 * IQR# 檢測異常值outliers = df[(df[column] < lower_bound) | (df[column] > upper_bound)]print(f'在 {column} 中檢測到 {len(outliers)} 個異常值')# 可視化前后對比plt.figure(figsize=(12, 4))plt.subplot(1, 2, 1)sns.boxplot(y=df[column])plt.title(f'原始 {column}')# 封頂異常值df[f'{column}_capped'] = np.where(df[column] > upper_bound, upper_bound,np.where(df[column] < lower_bound, lower_bound, df[column]))plt.subplot(1, 2, 2)sns.boxplot(y=df[f'{column}_capped'])plt.title(f'封頂后的 {column}')plt.tight_layout()plt.show()return dfdf = detect_and_handle_outliers(df, 'displacement')
在 displacement 中檢測到 1 個異常值

特征縮放(標準化)
# 3. 特征縮放示例
# 原始數據
numeric_cols = ['weight', 'acceleration', 'displacement']
print('原始數據:')
print(df[numeric_cols].head())# 標準化
scaler = StandardScaler()
df_std = df.copy()
df_std[numeric_cols] = scaler.fit_transform(df[numeric_cols])# 最小-最大縮放
minmax = MinMaxScaler()
df_minmax = df.copy()
df_minmax[numeric_cols] = minmax.fit_transform(df[numeric_cols])print('\n標準化數據 (均值=0, 標準差=1):')
print(df_std[numeric_cols].head())print('最小-最大縮放數據 (范圍 [0,1]):')
print(df_minmax[numeric_cols].head())
原始數據:weight acceleration displacement
0 2400 15.5 140
1 3000 14.0 200
2 4300 12.5 360
3 2500 16.0 150
4 2200 15.0 130標準化數據 (均值=0, 標準差=1):weight acceleration displacement
0 -0.820462 0.854242 -0.489225
1 -0.149175 0.000000 -0.443360
2 1.305280 -0.854242 -0.321054
3 -0.708580 1.138990 -0.481581
4 -1.044224 0.569495 -0.496869
最小-最大縮放數據 (范圍 [0,1]):weight acceleration displacement
0 0.090909 0.9 0.002801
1 0.363636 0.6 0.019608
2 0.954545 0.3 0.064426
3 0.136364 1.0 0.005602
4 0.000000 0.8 0.000000
箱線圖可視化
import matplotlib.pyplot as plt
import seaborn as snsplt.figure(figsize=(8, 5))
sns.boxplot(data=df[['mpg', 'weight', 'acceleration']])
plt.title("數值特征的箱線圖")
plt.show()

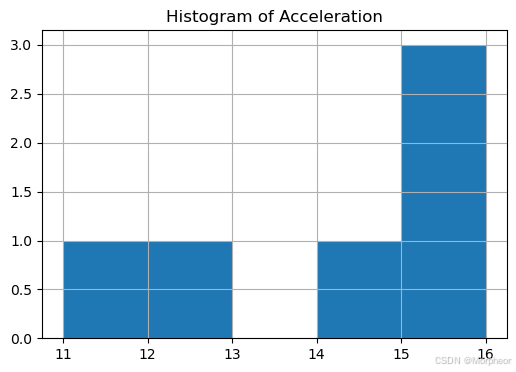
直方圖
df[['acceleration']].hist(bins=5, figsize=(6, 4))
plt.title("加速直方圖")
plt.show()
散點圖
sns.scatterplot(x='weight', y='mpg', data=df)
plt.title("散點圖:重量 vs 每加侖英里數")
plt.show()

交叉表
pd.crosstab(df['origin'], df['cylinders'])
| cylinders | 4 | 6 | 8 |
|---|---|---|---|
| origin | |||
| 1 | 1 | 1 | 2 |
| 2 | 1 | 0 | 0 |
| 3 | 1 | 0 | 0 |
降維(主成分分析)
# 4. 降維示例
# 準備PCA數據
X = df[['weight', 'acceleration', 'displacement_capped']]
y = df['mpg']# 首先標準化數據
X_scaled = StandardScaler().fit_transform(X)# 應用PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)# 創建主成分的新數據框
df_pca = pd.DataFrame(data=X_pca, columns=['PC1', 'PC2'])
df_pca['mpg'] = y.values# 繪制結果
plt.figure(figsize=(8, 6))
scatter = plt.scatter(df_pca['PC1'], df_pca['PC2'], c=df_pca['mpg'], cmap='viridis')
plt.xlabel('第一主成分')
plt.ylabel('第二主成分')
plt.colorbar(scatter, label='每加侖英里數')
plt.title('汽車特征的PCA')
plt.show()print(f'解釋方差比例: {pca.explained_variance_ratio_}')
print(f'總解釋方差: {sum(pca.explained_variance_ratio_):.2f}%')

解釋方差比例: [0.95929265 0.02632386]
總解釋方差: 0.99%
特征選擇
如果通過特征重要性技術發現 car_name 或 model_year 無關,我們可能會刪除它們。
)











)


)

)
)
