光譜數據分析是通過特征光譜識別物質結構與成分的核心技術，其標準化流程如下：

?一、數據預處理?（消除干擾噪聲）

?去噪平滑?

Savitzky-Golay濾波：保留光譜特征峰形，消除高頻噪聲。

移動平均法：適用于基線平穩場景。

?基線校正?

多項式擬合：消除儀器漂移（如紅外光譜基線偏移）。

自適應迭代加權：動態修正復雜背景。

?散射校正?

MSC（多元散射校正）：消除顆粒物散射效應（如粉末樣品）。

?歸一化處理?

SNV（標準正態變量變換）：解決光程差異問題。

矢量歸一化：提升光譜可比性。

?關鍵指標?：信噪比（SNR）提升≥20dB視為有效預處理。

?二、特征提取與篩選?（聚焦關鍵信息）

?三、建模與分析方法?

(1) ?定量分析模型?

?偏最小二乘回歸（PLSR）?：解決多重共線性問題（如潤滑油金屬含量檢測）。

?最小二乘支持向量回歸（LSSVR）?：處理非線性關系（精度提升8-12%）。

?校驗要求?：R2>0.9，RMSECV（交叉驗證均方根誤差）<5%。

(2)?分類識別模型

四、關鍵注意事項?

?基體效應規避?

檢測航空潤滑油需專用標樣，礦物油標樣會導致誤差>30%。

?動態范圍控制?

高濃度樣品需稀釋（如COD>200mg/L水體）防止信號飽和。

?模型泛化驗證?

每新增100樣本需更新校正集，采用10折交叉驗證。

?技術適配原則?

原子光譜：關注?線狀光譜?（如元素吸收峰）。

分子光譜：解析?帶狀光譜?（如官能團振動峰）。

光譜數據分析需根據?樣品屬性?（固態/液態/氣態）、?目標組分?（元素/分子）及?精度需求?動態選擇方法鏈，預處理與特征工程環節對結果可靠性影響超60%。

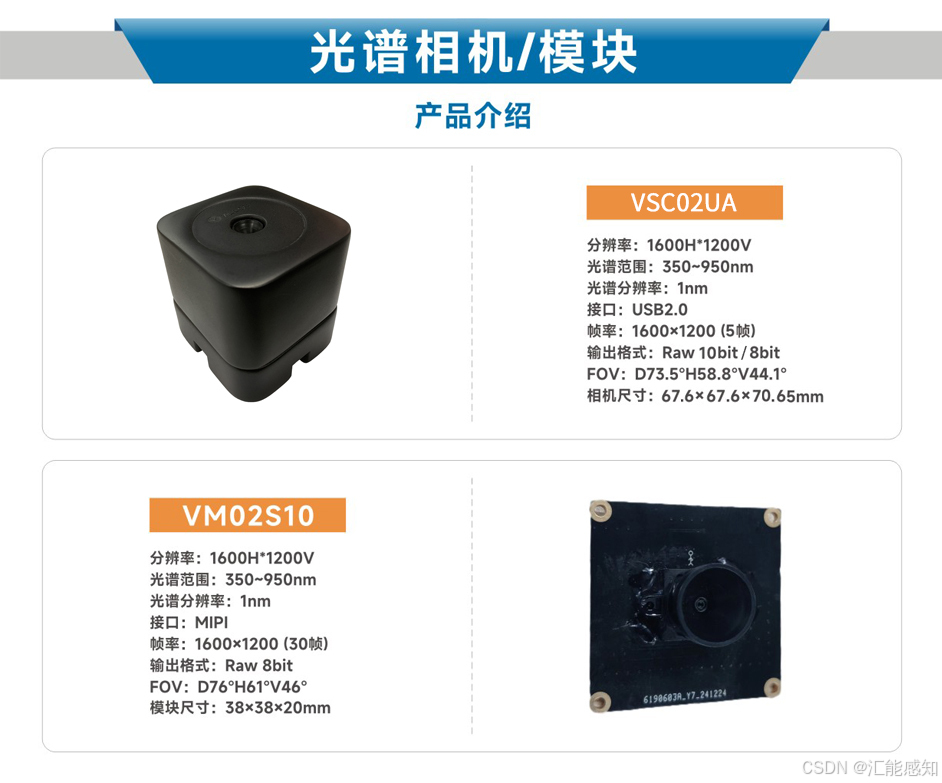
匯能感知光譜相機/模塊

👇點擊以下名片，獲取更多產品資料👇

歡迎咨詢，歡迎交流