MySQL 索引：為使用 B+樹作為索引數據結構，而非 B樹、哈希表或二叉樹？

在數據庫的世界里，性能是永恒的追求。而索引，作為提升查詢速度的利器，其底層數據結構的選擇至關重要。如果你深入了解過 MySQL（尤其是其主流存儲引擎 InnoDB），你會發現它不約而同地選擇了 B+樹 作為索引的主要實現方式。

這背后有什么深思熟慮的考量？為什么不是我們同樣熟悉的 B樹、查找效率驚人的哈希表，或者經典的二叉搜索樹呢？本文將帶你層層剖析，從磁盤I/O到查詢特性，徹底搞懂 MySQL 這項關鍵技術選型背后的智慧，并直觀對比它們之間的優劣。

核心問題：數據庫索引面臨的挑戰

在討論具體數據結構之前，我們首先要明白數據庫索引，特別是關系型數據庫中的索引，通常需要應對哪些挑戰：

數據量大，存儲在磁盤：數據庫中的數據通常遠超內存容量，大部分數據和索引都存儲在磁盤上。磁盤I/O操作相比內存操作要慢幾個數量級，因此，減少磁盤I/O是索引設計的首要目標。
查詢類型多樣：不僅有精確的等值查詢（如 WHERE id = 100），還有大量的范圍查詢（如 WHERE age BETWEEN 18 AND 30）、排序（ORDER BY）和模糊匹配（如 WHERE name LIKE '張%'）。
高并發與動態更新：數據庫需要支持高并發的讀寫操作，索引結構必須能夠高效地進行插入、刪除和更新，并在此過程中保持良好的性能。

帶著這些挑戰，我們來看看 B+樹為何能脫穎而出。

1. B+樹：為數據庫索引而生的王者

B+樹的結構特性一覽

B+樹是一種多路平衡搜索樹，它在B樹的基礎上進行了優化，特別適合磁盤等外部存儲設備：

多路分支 (高扇出性)：每個非葉子節點可以擁有大量子節點（通常成百上千），這使得樹的高度極低。
非葉子節點僅存儲鍵(Key)：非葉子節點（內部節點）只存儲索引鍵和指向下一層節點的指針，不存儲實際數據。這使得每個節點能容納更多鍵，進一步降低樹高。
所有數據存儲在葉子節點：所有數據記錄（對于聚簇索引是整行數據，對于二級索引是主鍵值）都存儲在葉子節點。
葉子節點形成有序鏈表：所有葉子節點通過指針串聯起來，形成一個有序的雙向鏈表，便于范圍查詢和順序掃描。
高度平衡：所有葉子節點都處于同一層級，確保了任何查詢的路徑長度基本一致，查詢性能穩定。

B+樹結構圖：

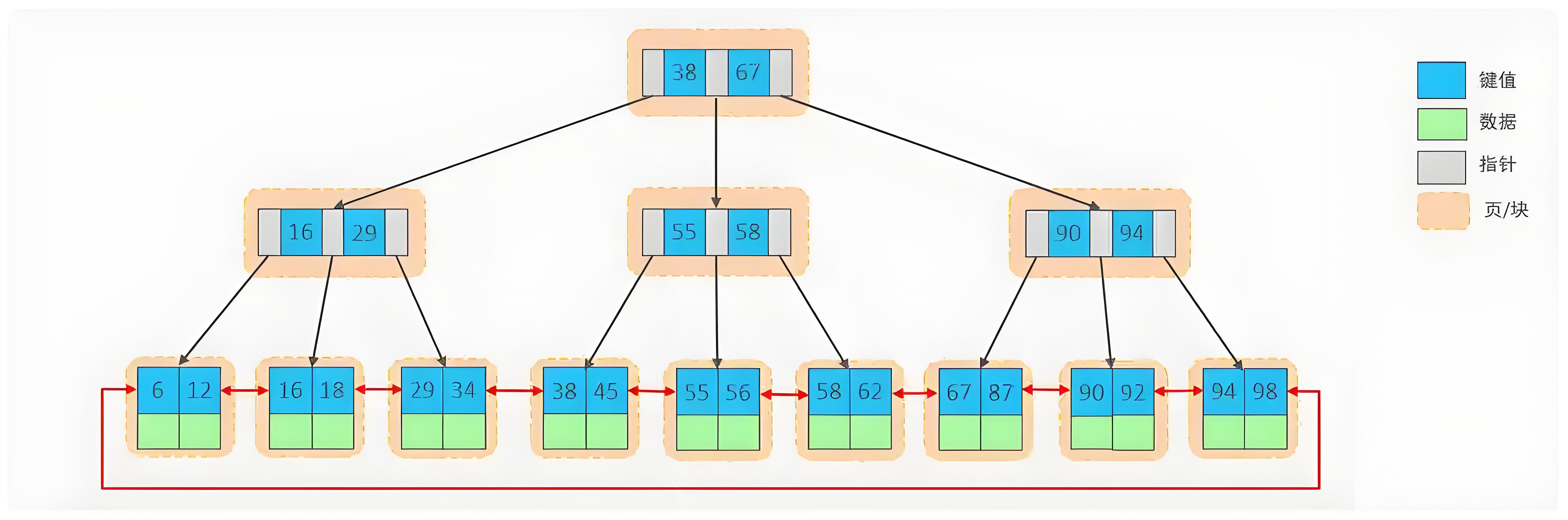B+樹在數據庫索引中的核心優勢

極低的樹高，顯著減少磁盤I/O：

這是B+樹最核心的優勢。由于非葉子節點不存數據，只存鍵和指針，單個節點（通常對應一個磁盤頁，如 InnoDB 默認16KB）可以容納非常多的鍵。例如，假設一個節點能存1000個鍵，那么一個存儲千萬級數據的B+樹索引，其高度可能只有 log????(10?) ≈ 2.33，也就是3到4層。這意味著一次查詢最多只需要3-4次磁盤I/O操作，性能極高。
高效的范圍查詢和順序掃描：

數據庫中范圍查詢（BETWEEN...AND..., >, <）非常普遍。B+樹的葉子節點通過雙向鏈表有序連接，當定位到范圍查詢的起點后，只需沿著鏈表順序（或逆序）遍歷即可獲取所有符合條件的數據，無需頻繁回溯樹結構，效率遠超其他結構。
充分利用磁盤預讀特性：

B+樹的葉子節點存儲數據的順序性，使得數據庫的預讀機制（如 InnoDB 的線性預讀）能發揮更大作用。當訪問一個葉子節點時，系統可以預先加載后續幾個葉子節點到內存，從而減少后續訪問的磁盤I/O。
高效的動態更新與平衡維護：

B+樹通過節點的分裂和合并機制，在插入和刪除數據時依然能保持樹的平衡，且這些操作的局部性較好，開銷相對可控，適合頻繁更新的數據庫環境。
聚簇索引與二級索引的良好支持：

在 InnoDB 中：
- 主鍵索引（聚簇索引）：葉子節點直接存儲完整的行數據。
- 二級索引（輔助索引）：葉子節點存儲索引列的值和對應行數據的主鍵值。查詢時先通過二級索引找到主鍵，再通過主鍵索引（回表）找到完整數據。這種設計使得非葉子節點更小，樹高更低。

2. 為什么不用 B樹 (B-Tree)？

B樹的結構特性

B樹也是一種多路平衡搜索樹，與B+樹的主要區別在于：

節點同時存儲鍵和數據：B樹的每個節點（無論是葉子節點還是非葉子節點）都存儲索引鍵以及對應的數據（或指向數據的指針）。
葉子節點間無鏈表：B樹的葉子節點之間通常沒有指針相連。

B樹的不足之處

范圍查詢效率較低：

由于數據分散在所有節點中（包括非葉子節點和葉子節點），進行范圍查詢時，B樹需要通過類似中序遍歷的方式來訪問所有符合條件的記錄。這個過程涉及到在樹的不同層級節點間的跳轉和回溯，無法像B+樹那樣僅通過遍歷葉子節點層的有序鏈表來高效完成。這往往意味著更多的隨機磁盤I/O。

舉例來說：B樹的范圍查詢本質上是對樹進行遞歸的中序遍歷（訪問左子樹 -> 處理當前節點的數據 -> 訪問右子樹），以確保按鍵的順序訪問所有符合范圍的記錄。
- 假設一個B樹的某個非葉子節點存儲了鍵 [50]（以及對應的數據），其左子節點指向的子樹包含鍵范圍如 [30-49]，右子節點指向的子樹包含鍵范圍如 [51-70]。
- 當我們要查詢鍵在 35 到 65 之間的所有記錄時：
  1. 首先，算法會深入左子樹，找到并處理 35 到 49 之間的記錄。
  2. 當左子樹中所有符合條件的記錄處理完畢后，需要回溯到包含鍵 50 的這個父節點，處理鍵 50 對應的數據（因為它在 35-65 范圍內）。
  3. 接著，算法再進入右子樹，繼續查找并處理 51 到 65 之間的記錄。
- 這里的“回溯”指的是在遍歷完一個分支（如左子樹）后，需要返回到其父節點，處理父節點自身的數據（如果符合條件），然后再去探索其他分支（如右子樹）。這種跨層級、非連續的訪問模式，在數據量大且存儲在磁盤上時，會顯著增加尋道時間和I/O次數，尤其與B+樹葉子節點純粹的順序掃描相比，效率差距明顯。
磁盤I/O次數可能更多 (樹高可能更高)：

因為非葉子節點也存儲數據（或數據指針），這占用了節點內寶貴的空間。在相同的節點大小下，B樹的非葉子節點能容納的鍵數量會少于B+樹。這意味著B樹的“扇出”（一個節點能擁有的子節點數）可能更小，從而導致樹的高度相對B+樹更高，查詢時需要的磁盤I/O次數隨之增加。
順序訪問性能差：

缺乏葉子節點鏈表，使得B樹在進行全表掃描或大范圍的順序數據訪問時，效率不如B+樹。

小結：B樹在單點查詢上性能可能與B+樹接近，但數據庫中大量的范圍查詢和對磁盤I/O的極致追求，使得B+樹的特定優化（非葉子節點不存數據、葉子節點鏈表）更具優勢。

3. 為什么不用哈希表 (Hash Table)？

哈希表的結構特性

哈希表通過哈希函數將鍵（Key）映射到一個桶（Bucket）中，理想情況下，查找、插入、刪除的時間復雜度可以達到 O(1)。

哈希表的致命缺陷

不支持范圍查詢：

這是哈希表作為數據庫主索引的最大硬傷。哈希函數會將相鄰的鍵值映射到不相鄰的存儲位置，數據是無序存儲的。因此，對于 WHERE id > 100 這樣的范圍查詢，哈希表無能為力，只能進行全表掃描。
不支持前綴查詢和排序：

類似于范圍查詢，對于 WHERE name LIKE 'abc%' 這樣的前綴匹配，或者 ORDER BY column 這樣的排序需求，無序的哈希表也無法高效支持。
哈希沖突問題：

當不同的鍵通過哈希函數計算出相同的哈希值時，就會發生哈希沖突。解決沖突（如鏈地址法、開放地址法）會帶來額外的開銷。在數據量大或哈希函數設計不佳時，沖突可能變得嚴重，使性能從 O(1) 退化到 O(n)。
動態擴展成本高：

當數據量增加，哈希表需要擴容（增加桶的數量）以維持性能時，通常需要對所有數據進行 Rehash 操作，這個過程非常耗時。

MySQL 中的哈希索引：

值得注意的是，MySQL 的某些存儲引擎（如 Memory 引擎）確實支持顯式的哈希索引。此外，InnoDB 引擎有一個“自適應哈希索引（Adaptive Hash Index, AHI）”特性，它會監控B+樹索引的查找模式，如果發現某些索引值被頻繁等值訪問，InnoDB 會在內存中為這些熱點頁建立哈希索引，以加速等值查詢。但這是一種輔助手段，底層的永久索引仍然是B+樹。

小結：哈希表在等值查詢場景下速度極快，但無法滿足數據庫多樣化的查詢需求，尤其是范圍查詢和排序。

4. 為什么不用二叉樹 (及其變種，如AVL樹、紅黑樹)？

二叉樹的結構特性

二叉搜索樹（BST）及其平衡變種（如AVL樹、紅黑樹）每個節點最多有兩個子節點。它們在內存中的查找效率很高，時間復雜度為 O(log?n)。

二叉樹的磁盤瓶頸

樹高過高，導致大量磁盤I/O：

這是二叉樹不適用于磁盤存儲作為主索引的根本原因。由于每個節點分支有限（最多兩個），對于海量數據，樹的高度會非常大。例如，存儲1000萬條記錄，二叉樹的高度約為 log?(10?) ≈ 23.25，即大約24層。這意味著一次查詢可能需要多達24次磁盤I/O，這在數據庫應用中是無法接受的，而B+樹通常只需3-4次。
磁盤頁利用率低下：

數據庫從磁盤讀取數據是按“頁”（Page，如 InnoDB 默認16KB）為單位的。二叉樹的一個節點只存儲一個鍵、數據（或指針）和兩個子節點指針，遠未填滿一個磁盤頁，造成了大量的空間浪費和I/O浪費。而B+樹的一個節點可以存儲成百上千個鍵，充分利用了磁盤頁的存儲能力。
范圍查詢不友好：

雖然平衡二叉樹可以通過中序遍歷實現范圍查詢，但其過程涉及大量非順序的節點訪問，無法像B+樹葉子節點鏈表那樣高效。
平衡維護的復雜性（針對磁盤）：

像AVL樹這樣的強平衡二叉樹，在插入刪除時可能需要頻繁的旋轉操作來維持平衡。這些旋轉在內存中尚可，但在磁盤上可能引發多次、分散的I/O操作。

小結：二叉樹（包括其平衡變種）是優秀的內存數據結構，但其結構特性導致在面對磁盤存儲和海量數據時，I/O瓶頸過于突出，不適合作為數據庫的主流索引結構。

直觀對比總結：群雄逐鹿，B+樹勝出

為了更清晰地展示這幾種數據結構的特點及其在數據庫索引場景下的適用性，我們總結如下表：

特性/數據結構	B+樹 (MySQL InnoDB)	B樹	哈希表	二叉樹 (平衡)
基本結構	多路平衡搜索樹	多路平衡搜索樹	哈希函數+數組/鏈表	最多兩路平衡搜索樹
存儲方式	非葉存鍵，葉存數據/主鍵	所有節點存鍵+數據	鍵值對，無序	節點存鍵+數據
磁盤I/O	極低 (樹高矮)	低 (樹高可能略高)	通常低 (沖突時增加)	極高 (樹高)
單點查詢	O(log<sub>m</sub>N)	O(log<sub>m</sub>N)	O(1) (理想情況)	O(log?N)
范圍查詢	高效 (葉子鏈表)	中等 (需遍歷樹)	極差 (不支持)	中等 (中序遍歷)
順序訪問	高效	一般	極差	一般
前綴查詢	支持	支持	不支持	支持
排序支持	高效	一般	不支持	一般
空間利用率	高 (節點復用好)	中等 (數據分散)	取決于沖突和填充因子	低 (針對磁盤頁)
動態更新	高效 (分裂/合并)	高效 (分裂/合并)	復雜 (沖突/擴容成本高)	復雜 (旋轉，對磁盤不友好)
適用場景	數據庫通用索引	文件系統、部分數據庫	緩存、特定內存數據庫索引	內存查找