NLP學習路線圖（十六）：N-gram模型

一、為何需要語言模型？概率視角下的語言本質

自然語言處理的核心挑戰在于讓機器“理解”人類語言。這種理解的一個關鍵方面是處理語言的歧義性、創造性和結構性。語言模型（Language Model, LM）為此提供了一種強大的數學框架：它賦予任何詞序列一個概率，用以衡量該序列在真實語言中出現的可能性。

1.1 語言模型的核心任務

評估序列合理性：判斷一個句子“The cat sat on the mat”是否比“Mat the on sat cat the”更像人話。
預測下一個詞：給定上文“I have a dream...”，預測下一個最可能出現的詞（如“that”）。
生成連貫文本：基于概率采樣，逐步生成新的、語法語義合理的句子。

1.2 統計語言模型的興起

在早期NLP中，基于規則的方法試圖用語法書般的精確規則描述語言，但很快遇到瓶頸：人類語言充滿例外、方言和動態變化，規則難以窮盡。統計語言模型應運而生，其核心理念是：

“一個詞出現的可能性，可以由它在大量文本數據中出現的頻率來估計。”

N-gram模型正是這一理念最直接、最成功的實現之一。

二、N-gram模型：概念與數學基礎

2.1 核心定義

N-gram：指文本中連續出現的N個詞（或符號）單元。例如：
- Unigram (1-gram):?["the"], ["cat"], ["sat"]
- Bigram (2-gram):?["the", "cat"], ["cat", "sat"]
- Trigram (3-gram):?["the", "cat", "sat"]
N-gram語言模型：一個基于馬爾可夫假設的統計模型，它假設一個詞出現的概率僅依賴于它前面的有限個詞（通常是N-1個）。這是對現實語言復雜依賴關系的一種簡化，但實踐證明非常有效。

2.2 數學建模：鏈式法則與馬爾可夫假設

語言模型的目標是為整個詞序列W = (w1, w2, ..., wm)?賦予概率P(W)。根據概率的鏈式法則：
P(W) = P(w1) * P(w2|w1) * P(w3|w1, w2) * ... * P(wm|w1, w2, ..., wm-1)

精確計算P(wm|w1, w2, ..., wm-1)需要知道所有可能的歷史組合的概率，這在數據有限時幾乎不可能。馬爾可夫假設提供了簡化方案：假設一個詞的概率只依賴于前面有限的k個詞。當k = N-1時，我們得到N-gram模型：

P(wm|w1, w2, ..., wm-1) ≈ P(wm|wm-N+1, wm-N+2, ..., wm-1)

因此，序列概率近似為：
P(W) ≈ Π P(wi|wi-N+1, ..., wi-1)

2.3 概率估計：最大似然估計（MLE）

模型參數P(wi|wi-N+1, ..., wi-1)如何獲得？最直觀的方法是在大型訓練語料庫中計數：

P(wi | wi-N+1, ..., wi-1) = Count(wi-N+1, ..., wi-1, wi) / Count(wi-N+1, ..., wi-1)

Count(wi-N+1, ..., wi-1, wi)：特定N-gram序列在語料中出現的次數。
Count(wi-N+1, ..., wi-1)：該序列的歷史上下文（前N-1個詞）出現的次數。

示例：?在語料“the cat sat on the mat”中：

P(sat | the cat) = Count(the cat sat) / Count(the cat) = 1 / 1 = 1.0
P(mat | on the) = Count(on the mat) / Count(on the) = 1 / 1 = 1.0

三、構建N-gram模型：從數據到應用

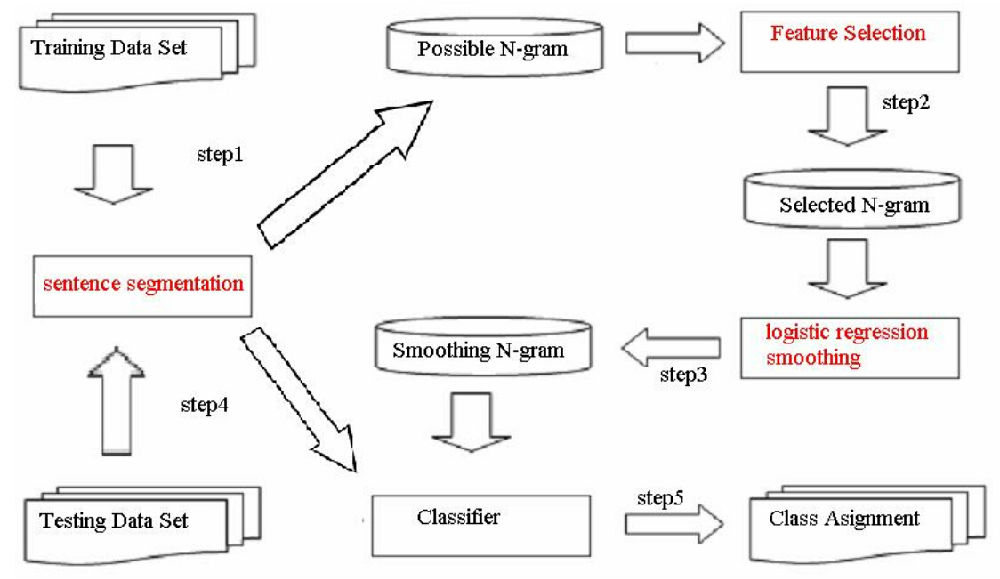
3.1 訓練流程

數據收集與預處理：收集大規模、領域相關的文本數據。進行分詞、去除標點/數字（可選）、統一大小寫、處理OOV詞（如替換為<UNK>）。
計數統計：掃描語料，統計所有1-gram, 2-gram, ..., N-gram的出現頻次。通常使用高效的數據結構（如哈希表、前綴樹）。
概率計算：應用MLE公式計算所有條件概率P(wi | context)。
平滑處理（關鍵！）：處理零概率問題（見下一節）。
模型存儲：存儲計算好的概率表（通常很大，需優化）。

3.2 解碼與應用：預測與生成

下一個詞預測：給定上下文(wi-N+1, ..., wi-1)，查找概率P(w | wi-N+1, ..., wi-1)最大的詞w。
序列概率評估：利用鏈式法則計算整個序列的概率（通常取對數避免下溢）。
文本生成：
1. 給定起始詞（或<S>標記）。
2. 基于當前上下文（最后N-1個詞），根據概率分布P(w | context)采樣下一個詞。
3. 將采樣詞加入序列，更新上下文。
4. 重復步驟2-3，直到生成結束標記</S>或達到長度限制。

四、挑戰與對策：平滑技術詳解

MLE估計的最大問題是數據稀疏性：語料庫再大，也無法覆蓋所有可能的N-gram組合。未在訓練集中出現的N-gram（零頻問題）會直接導致概率為零，進而使整個序列的概率為零，這顯然不合理。平滑（Smoothing）?技術通過“劫富濟貧”來解決此問題。

4.1 核心思想

為所有可能的N-gram（即使未出現）分配非零概率。
從高頻N-gram的概率中“借”一小部分，分配給低頻或零頻N-gram。
確保所有概率之和為1。

4.2 常用平滑方法

加一平滑（拉普拉斯平滑）：
- 最簡單直觀。
- 公式：P(wi | wi-N+1, ..., wi-1) = (Count(wi-N+1, ..., wi-1, wi) + 1) / (Count(wi-N+1, ..., wi-1) + V)
- V：詞匯表大小。
- 優點：實現簡單。
- 缺點：對高頻N-gram概率削減過多；對于大N或大V，分配的概率太小，效果常不理想。
加K平滑（Lidstone平滑）：
- 加一平滑的推廣，加一個小的常數k(0 < k < 1)。
- 公式：P = (Count + k) / (Count_Context + k * V)
- 通過調整k可以在偏差和方差間取得平衡。
古德-圖靈估計（Good-Turing）：
- 更智能的平滑。核心思想：用觀察到的出現r次的N-gram數量，來估計出現r次的事物的總概率質量，并將其分配給未出現（r=0）的事物。
- 計算調整頻次：r* = (r+1) * N(r+1) / N(r)，其中N(r)是出現r次的N-gram類型數。
- 將頻次為0的N-gram概率估計為：P = N(1) / N（N是總token數）。
- 優點：理論基礎堅實，效果較好。
- 缺點：計算復雜，需統計所有頻次N(r)；對于高頻r，N(r)可能為0或不穩定。
回退（Backoff）：
- 核心思想：如果一個高階N-gram（如trigram）沒有數據，就“回退”到低階N-gram（如bigram或unigram）的估計。
- 條件：通常僅在Count(HighOrderNgram) = 0時觸發回退。
- 概率分配：高階概率為0時，使用低階概率乘以一個回退權重α（α < 1），以確保總概率質量守恒。
- 公式（以trigram回退到bigram為例）：
```
P(wi | wi-2, wi-1) = {Count(wi-2, wi-1, wi) / Count(wi-2, wi-1)   if Count(wi-2, wi-1, wi) > 0α(wi-2, wi-1) * P(wi | wi-1)               otherwise
}
```
- 權重計算：α需要精心設計，保證在wi-2, wi-1條件下，所有詞的概率和為1。
插值（Interpolation）：
- 核心思想：無論高階N-gram是否存在數據，總是將不同階（unigram, bigram, trigram, ...）的估計混合起來。
- 公式（以trigram插值為例）：
  P(wi | wi-2, wi-1) = λ1 * P(wi) + λ2 * P(wi | wi-1) + λ3 * P(wi | wi-2, wi-1)
- 約束：λ1 + λ2 + λ3 = 1，λi >= 0。
- 優點：更魯棒，即使高階gram有數據，低階gram也能提供有價值信息，防止過擬合。
- 權重學習：λ參數通常通過在留存數據集（held-out data）上優化模型困惑度（Perplexity）來學習。
Kneser-Ney平滑：
- 被廣泛認為是效果最佳的N-gram平滑方法之一，結合了回退和絕對折扣的思想。
- 核心創新（主要在unigram概率上）：
  - 延續概率（Continuation Probability）：低階模型（如unigram）不再僅基于詞頻，而是考慮一個詞出現在不同上下文類型中的多樣性。
  - 公式（以bigram Kneser-Ney為例）：
```
P_KN(wi | wi-1) = max(Count(wi-1, wi) - D, 0) / Count(wi-1)  + λ(wi-1) * P_Continuation(wi)
P_Continuation(wi) = |{v: Count(v, wi) > 0}| / |{(u, v): Count(u, v) > 0}|
```
  - D：折扣常數（通常0.75左右）。
  - λ(wi-1)：歸一化因子，保證概率和為1。
  - P_Continuation(wi)：衡量wi作為新上下文“接續詞”的能力。想象“Francisco”在“San Francisco”中頻率高，但單獨作為接續詞能力弱（主要接在“San”后）；而“cup”則可能出現在“coffee cup”, “world cup”等多種上下文中，其P_Continuation較高。
- 優點：顯著提高了對低頻詞和未知上下文的建模能力。
- 變種：Modified Kneser-Ney (MKN) 使用多個折扣值（對不同頻次）。

下表總結了主要平滑方法的比較：

平滑方法	核心思想	優點	缺點	適用場景
加一(拉普拉斯)	所有計數+1	實現極其簡單	高頻項概率削減過多，效果常不佳	教學示例，快速原型
加K平滑	所有計數 + k (0<k<1)	比加一靈活，可調參數	k值選擇需經驗或優化，高頻項仍被削	對簡單加一的改進
古德-圖靈	用出現r次類型數估計r*概率	理論基礎好，對零頻項估計合理	計算復雜，高頻估計不穩定	需要較好理論基礎的中小模型
回退	高階無數據時回退到低階	直覺清晰，實現相對直接	權重設計復雜，僅高階缺失時才用低階	資源受限，需顯式回退邏輯
插值	混合不同階模型，加權平均	更魯棒，充分利用各級信息	需學習權重參數，計算開銷稍大	追求最佳效果的通用場景
Kneser-Ney	折扣+回退+獨特接續概率	公認效果最好	實現最復雜，計算開銷最大	對性能要求高的生產系統

五、N-gram模型的應用場景

盡管相對“傳統”，N-gram模型憑借其高效、簡單和可解釋性，在眾多場景中仍有一席之地，或作為更復雜系統的組件：

文本輸入法：
- 核心應用！基于用戶輸入的前幾個詞（或拼音音節），預測下一個最可能的候選詞。
- Bigram/Trigram模型在此任務上非常高效且有效。
- 例如：輸入“wo xiang”，模型基于“我想”的歷史，高概率預測“吃”、“要”、“買”等詞。
拼寫檢查與語法糾錯：
- 檢測低概率詞序列。句子“I are a student”中“I are”的bigram概率會極低，觸發錯誤警報。
- 結合詞典和混淆集，用于建議糾正（如“are”-> “am”）。
語音識別：
- 聲學模型識別出多個可能的詞序列候選。
- 語言模型（通常是trigram或更高階）用于評估哪個詞序列在語言上更“合理”，對識別結果進行重排序。如“recognize speech” vs. “wreck a nice beach”。
機器翻譯（早期統計機器翻譯SMT）：
- SMT的核心組件之一（與翻譯模型配合）。用于評估翻譯輸出的目標語言流暢度。
- 生成的目標語言句子概率越高，通常意味著越流暢自然。
信息檢索：
- 查詢擴展：利用同文檔/相關文檔中的高頻共現詞（N-gram）擴展用戶原始查詢。
- 文檔排序：部分早期模型（如查詢似然模型）將文檔視為語言模型生成查詢的概率源，N-gram是其基礎。
- 相關性反饋：根據相關文檔中的顯著N-gram調整查詢。
文本分類與情感分析：
- 將N-gram（特別是unigram和bigram）作為強大的文本特征。
- 分類器（如Naive Bayes, SVM）學習不同類別（如體育/財經/娛樂；正面/負面）下N-gram特征的分布差異。
- 例如：“暴跌”、“漲停”、“市盈率”等bigram在財經類中概率高；“進球”、“射門”、“點球”在體育類中概率高。
生物信息學（DNA/蛋白質序列分析）：
- 將生物序列（A/T/C/G 或氨基酸）視為“文本”。
- N-gram模型用于識別保守序列模式、基因預測、序列比對等。

六、N-gram的局限性與現代NLP中的演變

6.1 固有局限性

數據稀疏性：核心挑戰，催生了平滑技術，但問題無法根除。長尾N-gram難以準確建模。
上下文窗口有限（馬爾可夫假設）：只能捕捉局部依賴（N-1詞），無法建模長距離依賴（如主謂一致跨越從句）。例如：“The?keys?to the cabinet?are?on the table” vs. “The?key?to the cabinets?is...”。
缺乏語義理解：基于共現統計，無法真正理解詞義、語義角色、邏輯關系。無法處理同義（“buy/purchase”）、反義（“hot/cold”）或隱喻。
維度災難：N增大時，可能的N-gram組合數量呈指數級增長（O(V^N)），導致存儲和統計需求爆炸。實踐中N很少超過5。
領域依賴性：在特定領域語料上訓練的N-gram模型，移植到其他領域效果會顯著下降（詞匯、表達方式不同）。

6.2 現代NLP中的傳承與演變

盡管有局限，N-gram的思想并未消亡，而是以不同形式融入現代NLP：

神經語言模型的基礎：
- Bengio在2003年提出的前饋神經網絡語言模型是神經語言模型的先驅。它使用詞嵌入表示詞，并通過神經網絡學習P(wi | wi-1, ..., wi-n+1)。它突破了離散表示和手工特征的局限，但仍基于固定窗口（N-gram）上下文。這直接啟發了后來的RNN/LSTM/Transformer。
子詞單元（Subword Units）：
- 現代模型（如BERT, GPT）普遍采用Byte Pair Encoding (BPE), WordPiece, Unigram LM等算法將詞分割為更小的子詞單元（如"un", "##able", "ization"）。
- 這些子詞單元本身可以看作是一種動態的、數據驅動的“N-gram”或字符組合，有效緩解了OOV問題和數據稀疏性，同時允許模型學習詞素級別的規律。
Transformer中的局部注意力（有時）：
- 雖然Transformer的自注意力機制原則上可以捕獲任意長距離依賴，但為了提高效率或引入歸納偏置，有時會使用受限（窗口）注意力。例如：
  - 局部窗口注意力：只關注當前位置前后固定窗口內的詞（如鄰居100個詞），這本質上是在學習一種軟化的、基于上下文的N-gram模型。
  - 稀疏注意力模式（如Longformer, BigBird）：包含局部窗口注意力作為其模式的一部分。
- 這些設計表明，局部依賴關系（N-gram的核心）在語言中仍然至關重要，并且高效捕獲它們仍然有價值。
特征工程的基石：
- 在深度學習模型中，N-gram特征（尤其是unigram, bigram）仍然常被作為輸入特征或與神經網絡的輸出拼接，為模型提供顯式的、強局部信號。例如，在文本分類或簡單序列標注任務中，N-gram特征結合神經網絡能取得很好效果。
輕量級解決方案與基線：
- 在資源受限（如嵌入式設備、低延遲場景）或數據量不大的任務中，平滑良好的N-gram模型因其極高的效率、低計算開銷和易于部署的特點，仍然是可行的選擇。
- 它也是評估更復雜模型進步的重要基線。如果一個強大的神經模型在某個任務上無法顯著超越精心調優的N-gram模型，可能意味著任務本身特性或模型設計存在問題。