數學分析——一致性(均勻性)和收斂

1. 連續函數

1.1?? 連續函數的定義

1.2?? 連續函數的性質

1.2.1? 性質一

1.2.2? 性質二

1.2.3? 性質三

1.2.4? 性質四

2. 一致連續函數

2.1?? 一致連續函數的定義

2.2?? 一致連續性定理(小間距定理)(一致連續函數的另一種定義)

2.3?? 一致連續性判定法

2.4?? 連續函數與一致連續函數的區別

3. 函數的序列和級數(無窮和)的一致收斂性

3.1?? 逐點收斂的定義

3.2?? 一致收斂的定義

3.3?? 一致收斂的Cauchy充要條件

3.4?? 一致收斂函數序列的性質

3.4.1? 有界性

3.4.2? 連續性

3.4.3? 可微性

4. 級數(無限項之和)

1. 連續函數

1.1?? 連續函數的定義

???????? 通俗地講，連續函數就是在附近點取得附近值的函數。

定義 1.1? 令 f ：A ? ?? ?為一個映射，其中 A ? ?? ，并假設? c∈A? 。若對于每一個 ε > 0 ，都存在一個 δ > 0 ，使得只要?

?????????? | x - c | < δ?? ?，就有 ??| f (x) - ?f (c) | < ε? ,

則稱函數 f 在? c 處是連續的。若 f 此函數在 A 的每一點都連續，則稱此函數在 f 上是連續的。若函數在 B 的每一個點處連續，則函數在? B ? A? 上連續。

??? 某一點的連續性定義可以用鄰域來表述如下。

定義 1.2? 令 f ：A ? ?? ?為一個映射，其中 A ? ?? ，并假設? c∈A? 。若對于 f (c) 的每一個鄰域 V ，都存 c 的一個領域 U ，使得只要?

?????????? x∈ A∩U? ?，就有 ??f (x)∈ V? ,

則稱函數 f 在? c 處是連續的。

??? 兩種定義是等價的。ε-δ ?定義法對應V 是 f (c) 的一個 ε 領域而? U 是 c 的一個? δ 領域的情況。

???????? 注意，為了定義 f? 在? c 點處的連續性，點 c 必須屬于 f? 的定義域 A ?。若點 c 是 A? 的一個孤點(注：在定義域中只有一個點)，則連續的條件自動成立，因為對于足夠小的 δ? > 0 ，滿足 | x - c | < δ?? 的唯一點就是 x =? c? ??，則? 0 = | f (x) - f (c)| < ε? 。因此函數在其定義域的每一個孤點都連續，因此孤點不太有趣。

??? 若? c∈A ?是 A? 的一個聚點(accumulation point)，則? f? 在? c 點處的連續性等價于條件

$\displaystyle \lim_{x \rightarrow c}{f(x)}=f(c)$ ?

其指的是，f? 隨著 x ? c?? 的極限存在，并且恰好等于f? 在? c 點處的函數值。

1.2?? 連續函數的性質

1.2.1? 性質一

???????? 若 ?f ,g ：A ? ?? ?在 c∈A ?處是連續的且? k∈?? ，則? kf ，f + g? 和 ?fg ?在 c? 處是連續。此外，若 g(c) ≠ 0 ，則 f /g 在 c? 處是連續的。

1.2.2? 性質二

???????? 每一個多項式函數在 ? 上都是連續的， 每一個比率函數在其定義域內都是連續的。

1.2.3? 性質三

???????? 令 ??f ：A ? ?? ?和 ?g ：B ? ?? ?為兩個映射，且? f (A) ? ?B? ?。若 ?f?? 在 c∈A ?處連續而 g? 在? f (c)∈B? ?處連續，則? g ○ f ：A ? ? 在 ?c∈A ?處連續。(○ 表示復合函數。)

1.2.4? 性質四

令 ??f ：A ? ?? ?和 ?g ：B ? ?? ?為兩個映射，且? f (A) ? ?B? ?。若 ?f?? 在 A ?上連續而 g? 在? f (A) 上連續，則? g ○ f ?在A 上連續。(○ 表示復合函數。)

2. 一致連續函數

???????? 一致連續性是一種微妙但有力的連續性增強。

2.1?? 一致連續函數的定義

定義 2.1? 令 f ：A ? ?? ?為一個映射，其中 A ? ?? ，并假設? c∈A? 。若對于每一個 ε > 0 ，都存在一個 δ ?> 0 ，使得只要?

?????????? | x - y | < δ?? ?且? x ，y∈A? ，就有 ??| f (x) - ?f (y) | < ε? ,

則稱函數 f 在 A 上是一致連續的。

也就是說，這樣的 δ?? 對于任意的 ε 都適用，不管你ε 多小，我這個 δ?? 都適用。

???????? 這個定義的關鍵點在于，δ ?僅取決于 ε ，而與 x ?和y無關，也就是說 x ?和y ?是任意兩點 。一個在A的每一點一致連續的函數必定在 A的每一點連續，但反之不成立。

例子1：函數?? $f(x)=\frac{1}{x}$ ??在 (0,+ ∞) 上是連續的，如下圖所示：

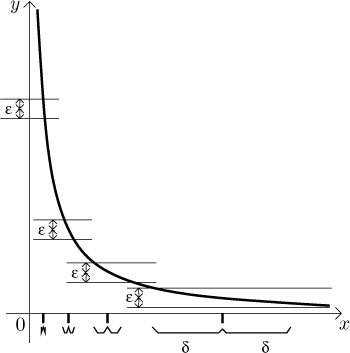
但其在此區間上不是一致連續的。從圖上直觀地可以看出，找不到一個對于已知 ε ?和任意兩點都成立的 δ ?。? 事實上，在圖中我們試圖表明，給定一個特定的 ε，我們被迫使 δ ?越來越小才??能贏得這個 ε的比賽，因為我們會使用更接近 0 的 y ，而且似乎這個過程不會停止，沒有 δ會普遍起作用。對于同樣一個? ε ，可以找到某個 δ ??在某個位置滿足 | x - y | < δ ?，但當往 0 移動的時候，這個函數差值就會大于 ε ，因此這個 δ 不能對所有 ε ?都成立。

???????? 但若我們將此函數的定義域限定為 [1 ,+ ∞) ，則此函數是一致連續的。如下圖所示

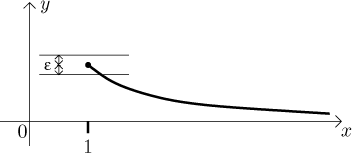
我們可以在“末端”取得這個 δ ??，使其對于所有的 ε 都成立。也就是說，如果任意給一個 ε? ，如果我這個 δ ??取在末端，不管你這個 | x - y | 位置怎么擺動，都能滿足一致收斂條件。這個是理解的難點。

2.2?? 一致連續性定理(小間距定理)(一致連續函數的另一種定義)

??? 令 f 為一個實函數且在閉區間 [a,b] 上連續，并令 M( f ) 和 m( f ) 分別表示 f 在 [a,b] 上的最大值和最小值。我們稱其差值

??????????????? M( f ) - m( f )

為 f 在區間 [a,b] 上的間距或跨度(span)。一些作者使用術語擺距(oscillation)來代替間距，擺距的缺點是會讓人聯想到波動或波狀的函數。較早的文獻使用 saltus (急變)這個詞，其是leap對應的拉丁詞。“間距”這個詞似乎更能說明這里所度量的內容。我們注意到，[a,b] 的任意子區間中的 f 的間距都不會超越 f 在 [a,b] 中的間距。

可以證明，可以分割 [a,b] 使得f 在每一個子區間中的間距都任意小。更確切地說，我們有以下連續函數的小間距定理。在文獻中通常稱其為關于一致連續的小間距定理。

(關于一致連續的)小間距定理：令 f 為閉區間 [a,b] 上的一個連續函數。則對于每一個 ε > 0 ,存在 [a,b] 的一個有限數量的子區間分割，使得 f 在每一個子區間中的間隔小于 ε 。

2.3?? 一致連續性判定法

定理??? 令 [a,b] 為一個實數閉區間，f : [a,b]? ? 為一個連續函數。則 f ?在 [a,b] 上是一個一致連續函數。

說明：即閉區間上的連續函數必定一致連續，因為其可以在“端點處”取得適用于全局的 δ ??，即這種要求 δ ??越來越小才能滿足 ε 的趨拋是有盡頭的，如果這個區間無界，則對于有些函數而言，比如 1/x ，這種趨勢就沒有終點，無窮無盡。

2.4?? 連續函數與一致連續函數的區別

??? 當我們討論一個函數 f 在某點連續的時候，我們關注的僅僅是函數在此點附近的值的行為。一致連續是一個比連續更強的性質，是做某些擴展的時候基本的要求。就比如函數?? $f(x)=\frac{1}{x^{2}-2}$ ??，當定義有比率數(有理數)上的時候，它是成立的，但如果擴展到實數上，它則是不成立的。?

但當我們考慮函數 f 在其定義域上一致連續的時候，我們需要知道f在整個定義域上的值。因此連續性是一個局部性的概念，而一致連續是一個全局概念。所以針對一個點討論一致連續是沒有意義的。

??? 一致連續定義在一個集合上；不同于連續性，其沒有局部對應特性。一致連續確保了當在定義域上滑動的時候，定義在無界區間或復雜集合上的函數不會劇烈地無限振蕩，而定義在閉區間上的連續函數由于可以取得端點，函數是有界的，其振蕩有限。一致連續性在數學的各個領域都至關重要，包括分析、拓撲和度量空間。它用于涉及收斂、積分和微分的證明，一致連續函數可擴展性的一個典型應用是逆Fourier變換公式的證明。

3. 函數的序列和級數(無窮和)的一致收斂性

??? 函數序列的收斂性有許多不同的定義方式，不同的定義會導致不等價的收斂類型。我們在此考慮兩種基本類型：逐點收斂和一致收斂。

3.1?? 逐點收斂的定義

??? 逐點收斂用函數值在其定義域內每一點的收斂來定義函數的收斂，關注的是局部特性。

(逐點收斂)定義設? $(f_{n})$ ??是一個定義為? $f_{n}:A \rightarrow \mathbb{R}$ ??的函數序列，并設? f ：A ? ? 為另一個映射。則若對于每一個 x∈A ?，隨著? $n \rightarrow \infty$ 有? ? $f_{n} (x)\rightarrow f (x)$ ?，則稱按逐點收斂有 ? ? $f_{n} \rightarrow f(x)$ ?。

若? $f_{n}$ ??逐點收斂于 f? ?，則我們稱函數序列?? $(f_{n})$ ? 逐點收斂，在這種情況下有

$\displaystyle f (x) = \lim_{n \rightarrow \infty}{f_{n}(x)}$ ? 。

逐點收斂或許是定義函數收斂最直觀的方法，也是最重要的方法之一。然而，正如以下示例所示，它的表現并不像人們最初預期的那樣良好。

(1) 例1??? 假設? $f_{n} :(0,1) \rightarrow \mathbb{R}$ ??定義為?

$\displaystyle f_{n} (x) =\frac{n}{nx+1}$ ? ，

?由于 x ≠ 0 ， $\displaystyle \lim_{n \rightarrow \infty}f_{n}(x) = \lim_{n \rightarrow \infty} \frac{1}{x+1/n} = \frac{1}{x}$ ???，因此，? $f_{n} \rightarrow f$ ? ??是一致的，其中? f? ：(0,1) ? ?? ?定義為??

$\displaystyle f (x) = \frac{1}{x}$ ? ?。

?如圖：

(注：因此通過研究序列特性，就能預知其收斂到的函數的一些特性(如果收斂)。而研究序列更為容易。)

對于所有的 x∈(0,1)，我們有?? $|f_{n} (x)| < n$ ??, 因此，每一個 ? $f_{n}$ ?在 (0,1) 都是有界的，但這個逐點收斂的極限 f 不是有界的。因此，通常(僅)逐點收斂的函數序列不是保界的。

(2) 例2??? 假設映射? $f_{n} :(0,1) \rightarrow \mathbb{R}$ ?定義為? $f_{n} = x^{n }$ ??。若 0 ≤ x < 1 ，則隨著? $n \rightarrow \infty$ ??而有? $x^{n} \rightarrow 0$ ???，而若? x ?= 1 ，則? $n \rightarrow \infty$ ?而有? $x^{n} \rightarrow 1$ ??。因此按逐點收斂有? $f^{n} \rightarrow f$ ?，其中

$f(x)=\left \{ \begin{array}{lrc} 0\quad (\text{if}\; 0 \leq x <1),\\\\ 1\quad (\text{if}\; x=1) .\end{array} \right .$ ? ?

如圖：??

盡管函數序列?? $f_{n}$ ??在 [0,1] 上是連續的，但其逐點(收斂的)極限 f 卻不是連續的?(其在x = 1 處不連續)。?

(3) 例3 映射?? $f_{n}:[0,1] \rightarrow \mathbb{R}$ ??定義為

$f(x)=\left \{ \begin{array}{lrc} 2n^{2}x\quad (\text{if}\; 0 \leq x \leq \frac{1}{2n}),\\\\ 2n^{2}(\frac{1}{n}-x) \quad (\text{if}\; \frac{1}{2n}<x<\frac{1}{n}) , \\\\ 0\quad (\text{if}\; \frac{1}{n} \leq x \leq 1) . \end{array} \right .$ ?

若 0 < x ≤ 1 ，則對于所有 n ≥ 1/x? 則? $f_{n} (x) = 0$ ? ，因此隨著? $n \rightarrow \infty$ ?而有??? $f_{n} (x) \rightarrow 0$ ??；而若 ?x = 0 ，則對于所有 n ，? $f_{n} (x) = 0$ ?，因此也有?? $f_{n} (x) \rightarrow 0$ ??。可以推導出在? [0,1] 上? $f_{n} (x) \rightarrow 0$ ?是逐點的。即使隨著?? $n \rightarrow \infty$ ??而? $f_{n} (x)=n \rightarrow \infty$ ?也是如此。因此，逐點收斂函數序列 ? $(f_{n})$ ??不要求一致有界(即，其界與 n 無關)，即使它收斂于0。

(4) 例4?? 映射? $f_{n} :\mathbb{R} \rightarrow \mathbb{R}$ ?定義為?

$\displaystyle f_{n} (x) = \frac{\sin{(nx)}}{n}$ ?。

在 ? 上?? $f_{n} \rightarrow 0$ ?是逐點的。導數?? $f^{'}_{n}(x)=\cos{(nx)}$ ?的導數序列? $( f_{n}^{'} )$ ??在 ? 上并不一致收斂，例如

$f^{'}_{n}{(\pi)}=(-1)^{n}$ ??

并不隨著? $n \rightarrow \infty$ ?而收斂。因此，一般來說，逐點收斂序列無法微分。這種現象并不局限于逐點收斂序列，而是因為一個快速振蕩的小函數的導數可能很大。?

3.2?? 一致收斂的定義

??? 一致收斂是一個比逐點收斂更強的函數收斂概念。逐點收斂與一致收斂的區別類似于連續性與一致連續性的區別。

(一致收斂性)定義?? 設? $(f_{n})$ ?是一個定義為? $f_{n}:A \rightarrow \mathbb{R}$ ??的函數序列，并設? $f:A \rightarrow \mathbb{R}$ ??為另一個映射。則若對于每一個 ε > 0，都存在一個 N∈? ，使得對于任意的? x∈A ?，只要 n > N? ，就有

$|f_{n}-f|<\epsilon$ ?,

??則稱函數序列?? $f_{n}$ ??在 A 上隨著 $n \rightarrow \infty$ ??是一致收斂于 f ?的。通常，我們忽略其域 A ，稱?? $f_{n} \rightarrow f$ ??是一致的。

此定義的關鍵在于，N 僅取決于ε ，而不取決于 x ∈ A；而對于逐點收斂的序列，N 可能同時取決于ε和 x ?。一致收斂的序列始終逐點收斂(至同一極限)，但反之則不然。如果序列逐點收斂，則可能發生以下情況：對于某些ε > 0，可能需要為 x ∈ A 的不同點選擇任意大的 N，這意味著值序列會以任意緩慢的速度收斂于 A 。在這種情況下，逐點收斂的函數序列并非一致收斂。

??? 下面用兩例對比逐點收斂和一致收斂。

??? 一個連續函數序列的極限函數未必是連續函數(因為它不滿足一致收斂的條件)：

例如，對于函數序列?? $f_{n} (x) = \sin^{n}(x)$ ??，圖中綠曲線和藍色曲線所示，其在整個域上逐點收斂，但其極限函數是不連續的(圖中紅色所示)，因為此函數序列的振蕩幅度很大。因此，為了得到極限是一個連續的函數，我們就必須施加一致連續的要求。

而一致收斂函數序列示意圖如下：

3.3?? 一致收斂的Cauchy充要條件

(一致收斂的Cauchy充要條件)定義? ?設? $(f_{n})$ ??是一個定義為? $f_{n}:A \rightarrow \mathbb{R}$ ???的函數序列。則若對于每一個 ε > 0，都存在一個 N∈? ，使得對于任意的? x∈A ?，只要 m , n > N? (m , n ?均為正整數)，就有

$|f_{m} - f_{n} | < \epsilon$ ?，

則稱函數序列?? $f_{n}$ ??是一致 Cauchy ?函數序列。

定理(Cauchy一致收斂判別法) 設? $(f_{n})$ ?是一個定義為?? $f_{n}:A \rightarrow \mathbb{R}$ ??的函數序列。則當且僅當其 是 ?A 上的一個 一致收斂的 Cauchy 函數序列時其一致收斂。

3.4?? 一致收斂函數序列的性質

3.4.1? 有界性

定理? 假設?? $f_{n}:A \rightarrow \mathbb{R}$ ??對于 A 上的每一個? n∈? ?都是有界的，并且在 A 上? $f_{n} \rightarrow f$ ? ??

是一致的。則? f ：A ? ? ??在A 上是有界的。

具體而言，如果有界函數序列逐點收斂(而非一致收斂)于無界函數，則收斂不是一致收斂的。

3.4.2? 連續性

??? 一致收斂的一個最重要的屬性之一是其保連續性。

定理? 若一個連續函數族?? $f_{n}:A \rightarrow \mathbb{R}$ ??的序列 ? $(f_{n})$ ??在 ?A ? ? ?上一致收斂于函數 ? $f :A \rightarrow \mathbb{R}$ ?，則 ?f? 在 ?A 上連續。?如果一個連續函數序列逐點收斂于一個不連續函數，則該收斂不是一致(均勻)的。然而，反之則不成立，即使連續函數序列的收斂不是一致的，其逐點極限也可能是連續的，

3.4.3? 可微性

??? 可微函數的一致收斂通常并不意味著其導數的收斂或極限的可微性。可能因為兩個函數的值可能很接近，而它們的導數的值卻相距甚遠。因此，如果我們希望證明?? $f_{n} \rightarrow f$ ?意味著? $f_{n}^{'} \rightarrow f$ ??，就必須對一系列函數及其導數施加強條件。

定理? 假設? $(f_{n})$ ??是一個可微函數族 ?? $f_{n} :(a,b) \rightarrow \mathbb{R}$ ?的序列，且? $f_{n} \rightarrow f$ ?是逐點的，而 ? $f_{n}^{'} \rightarrow g$ ??對于某個 ??? $f , g : (a,b) \rightarrow \mathbb{R}$ ?是一致的。則 ?f ?在 ?(a,b) 上可微且? $f^{'}=g$ ? 。

4. 級數(無限項之和)

??? 級數的收斂性是根據其部分和序列(sequence of partial sums)(注：即前 n 部分項之和)的收斂性來定義的，任何關于序列的結果都可以很容易地轉化為相應的關于級數的結果。

定義? 假設?? $(f_{n})$ ?是一個定義為?? $f_{n}:A \rightarrow \mathbb{R}$ ??的函數序列。并令? $(S_{n})$ ??為由 ? $S_{n}:A \rightarrow \mathbb{R}$ ??定義的部分和序列。即部分和為

$\displaystyle S_{n} (x) = \sum_{k=1}^{n}f_{k} (x)$ ? ? 。

則在 A 上若? $S_{n} \rightarrow S$ ?隨著 ? $n \rightarrow \infty$ ?是逐點的，則 A 上級數????

$\displaystyle S(x) = \sum_{n=1}^{\infty}f_{n} (x)$ ? ? ?(注：無限序列之和)

A 上隨著 $n \rightarrow \infty$ ? 而逐點收斂于函數? S ：A ? ? ，且若在 ?A??上? ? $S_{n} \rightarrow S$ ??是致的，則級數一致收斂于 ?S ???。

定理? 令?? $(f_{n})$ ??是一個定義為? ? $f_{n} :A \rightarrow \mathbb{R}$ ??的函數序列。則對于一個級數

$\displaystyle \sum_{n=1}^{\infty}f_{n} (x)$ ? ，

當且僅且對于任意一個 ε > 0 ，都存在一個 N∈?? ，使得對于任意 ?x∈A ?和任意 n > m > N ，都有?

$\displaystyle \left |\sum_{k=m+1}^{n}f_{k} (x) \right | < \epsilon$ ? ，

則此級數一定收斂。

定理(Weierstrass M 收斂判別法)? 令 ?? $(f_{n})$ ??是一個定義為? ? $f_{n} :A \rightarrow \mathbb{R}$ ??的函數序列。并假設對于每一個 n∈?? ，都存在一個常數?? $M_{n} \geq 0$ ??使得