一、基礎知識
根據高中知識我們知道,很多函數都可以用泰勒級數展開。正余弦泰勒級數展開如下:
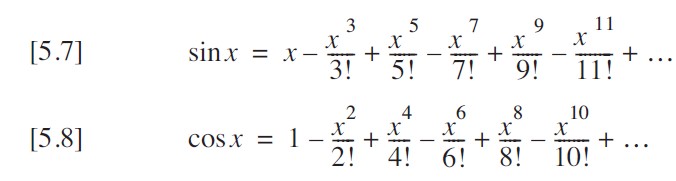
將其進一步抽象為公式可知:
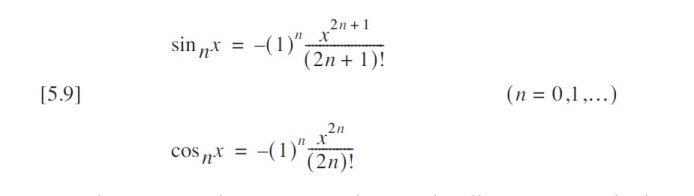
正弦和余弦的泰勒級數具有高度結構化的模式,可拆解為以下核心特征:
1. 符號交替特性
- 正弦級數:項的符號以
交替,即 +,?,+,?,…?
- 余弦級數:符號同樣由
控制,但首項為正(n=0 時),即 +,?,+,?,…
作用:正負項交替抵消了部分累積誤差,避免數值無意義地發散(如大角度場景中,若所有項同號,和會迅速溢出)。
2. 冪次規律
- 正弦:包含 x 的奇次冪(
…),對應通項中的 2n+1。
- 余弦:包含 x 的偶次冪(
…),對應通項中的 2n(注意
=1 為首項)。
直觀理解:正弦是奇函數(僅含奇次冪),余弦是偶函數(僅含偶次冪),與函數的奇偶性代數定義一致。
3. 分母的階乘主導
- 分母為分子指數的階乘,即奇次冪項分母為 (2n+1)!,偶次冪項為 (2n)!。
- 階乘的超指數增長:例如 10!=3,628,800,20!≈
,遠快于
的增長(即使 x 較大)。
關鍵作用:確保級數對任意 x 收斂,且小角度下項值急劇衰減(如 x=π/6 時,第 3 項已小于)。
????????在任何計算機數學的教科書或手冊中,你也都會找到這些函數的定義和相關性質。然而僅有公式并不足以在實際應用中解決問題。公式是基礎,但只有結合計算特性的優化,才能真正解決現實問題。
如果直接利用泰勒級數進行計算,將遇到幾方面的問題:
- 階乘的計算邊界:在編程中,n! 很快會超出數值類型范圍(如 32 位整數最大表示 20!),需使用浮點類型或大數庫,或通過遞推避免顯式計算階乘。
- 機器精度的限制:計算機無法表示無限精度,當項值小于機器的最小精度時,其對總和的貢獻在數值上為零,此時截斷級數是合理的。
????????無窮級數的問題在于它們…… 嗯…… 是無窮的。如果我有一臺無限算力的計算機和無限的時間,我現在就可以結束跳過后續的內容,關上電腦愉快的下班各回各家各找各媽了。
????????但在現實世界中,你不可能等待計算無窮多項。計算機也無法處理無限項計算。以 sin(1000) 為例,直接展開需數千項才能使階乘主導項衰減,而單精度浮點數在計算前幾項時就會因 xn 過大而溢出(如 =
,已接近單精度上限
)。幸運的是,你也不需要無限的精度。計算機中的任何實數都只是一個近似值,受限于計算機的字長。當計算機依次計算級數中的高階項時,這些項最終會變得小于計算機的位分辨率。在那之后,計算更多的項就毫無意義了。
????????在這個級數中,隨著 n 的增大,各項變得越來越小,但級數的和卻是無窮大。數學家們必然且確實會關注冪級數的收斂性;不過請放心,如果有人給出一個如 sin (x) 這樣的函數的級數展開式,他們必定已確保其收斂性。對于正弦和余弦函數,符號交替的特性確保了小項不會累積成大的數值。
????????如果高階項變得可以忽略不計,你可以截斷級數以獲得多項式近似。處理任何無窮級數時都必須這樣做。有時你可以估算引入的誤差,但大多數情況下,程序員只需保留足夠多的項,以確保誤差控制在合理范圍內。
????????通過一個例子來理解可能更直觀。表 5.1計算了 x=30°(即 π/6 弧度)的正弦和余弦值。在所示的精度范圍內,兩個級數在第五項后均已收斂(由于余弦項的每一項比正弦項少一個 x 的冪次,其收斂速度通常稍慢)。正如預期,由于分母中階乘的存在,各項的絕對值迅速減小。
| 項數n | 正弦項 | 正弦項累加和 |
| 0 | 0.52359878 | |
| 1 | 0.49980235 | |
| 2 | 0.50013697 | |
| 3 | 0.50013440 | |
| 4 | 0.50013441 | |
| 真實值 | sin(π/6)=0.5 | 誤差: |
| 項數n | 余弦項 | 余弦項累加和 |
| 0 | 1 | |
| 1 | 0.86292813 | |
| 2 | 0.86571844 | |
| 3 | 0.86568546 | |
| 4 | 0.86568585 | |
| 真實值 | cos(π/6)=0.8660254 | 誤差: |
????????對于三角函數的任何實際計算,最終結果都要求我必須限制 x 的范圍,就像我對平方根函數所做的那樣。顯然,范圍越小,所需的項數就越少。我還沒有向你展示如何限制范圍,但暫時假設這是可以做到的。那么需要多少項呢?
????????在這種情況下,計算所需的項數相當直接。由于級數中的項具有交替的符號,我不必擔心諸如許多小數項累加為大數之類的潛在問題。正如你在表 5.1 中看到的,中間結果圍繞最終結果振蕩。因此,我可以確定誤差總是小于(有時遠小于)第一個被忽略項的大小。我需要做的就是為角度范圍的代表性值計算方程中每個項的值,然后將結果與我所使用的數值表示中的最低有效位(LSB)精度進行比較。由于我無法預先知道你可能使用的數值格式,因此最好將這兩個步驟分開。項值如表 5.2 和 5.3 所示。請注意,對于更小的范圍,誤差減小得有多顯著。



?????????在表 5.4 和 5.5 中,我使用這些結果計算了典型計算機表示所需的項數。通常,預期尾數范圍為 24 位(32 位浮點數)或 56 位(C 語言雙精度使用的八字節格式)。較小的數值有時在專用嵌入式系統中有用,而最大的數值對應雙精度和數值協處理器的字長。同樣,只需看一眼這些表格,你就會相信,花一些計算能力來減少輸入參數的范圍是值得的。
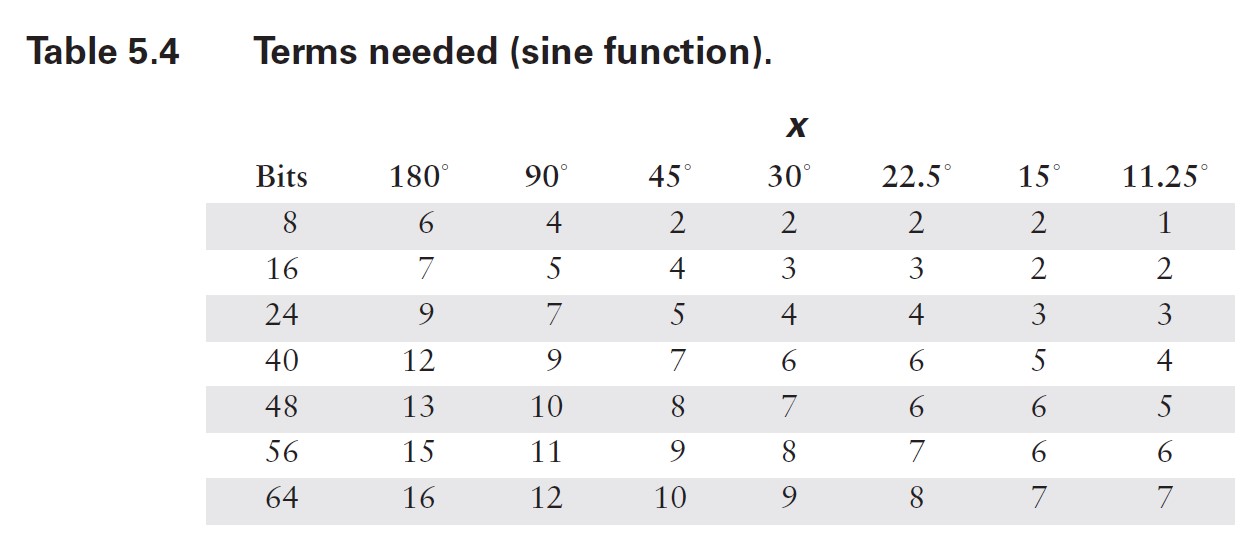
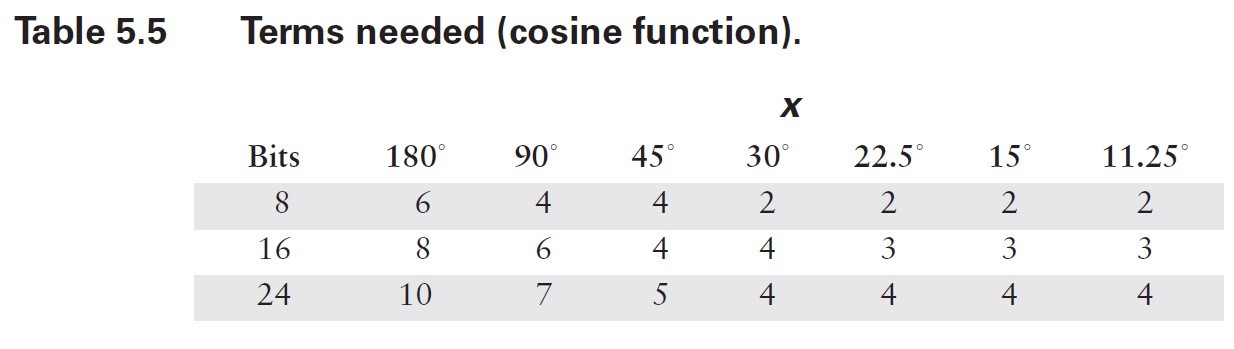
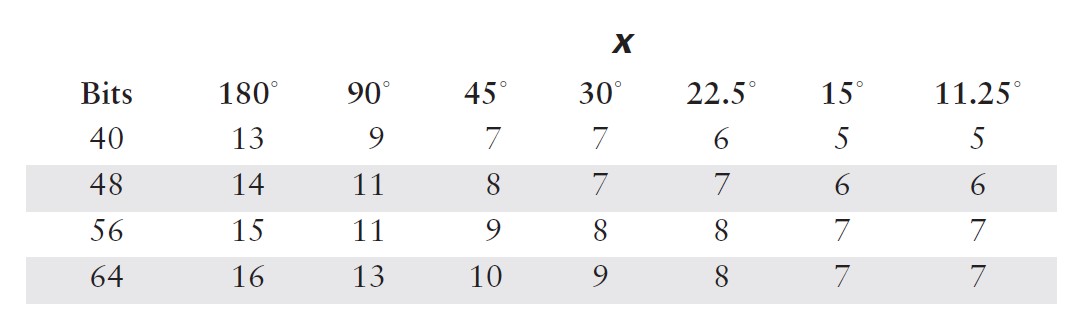
????????既然我已經知道需要在截斷級數中包含多少項,接下來仍需設計代碼對其進行計算。缺乏經驗的程序員可能會直接按方程 [5.7] 的寫法進行編程,為每一項反復計算和n!。一個簡單的停止準則可能只是將每一項的值與某個誤差準則進行比較(在這種情況下,表 5.2 至 5.5 并非必需)。
????????事實上,這正是我最初實現該函數的方式,只是為了證明自己能夠做到。這是一個糟糕的實現,因為它需要反復將x提升到越來越高的冪次,更不用說為每一項調用兩個耗時函數的開銷了。誠然,該函數對任何輸入(無論多大)都能給出正確答案,但付出的運行時性能代價卻非常高昂。
double factorial(unsigned long n){double retval = 1.0;for(; n>1; --n)retval *= (double)n;return retval;
}
double sine(double x){double first_term;double next_term = x;double retval = x;double sign = 1.0;double eps = 1.0e-16;int n = 1;do{cout << next_term << endl;first_term = next_term;n += 2;sign *= -1.0;next_term = sign * pow(x, n)/factorial(n);retval += next_term;
}while((abs(next_term) > eps));return retval;
}?????????通過觀察到每一項都可以由前一項遞推計算,我們可以顯著優化代碼效率。回顧方程 [5.9] 中正弦函數的通項公:

該級數的下一項時:
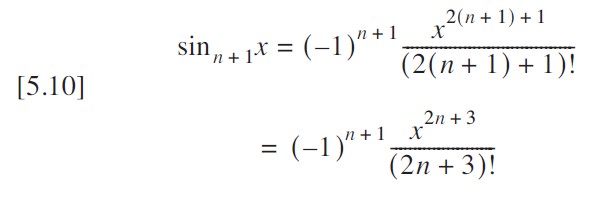
前后項相比知;
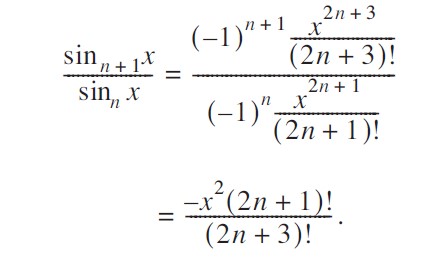
我們以代表其比值:
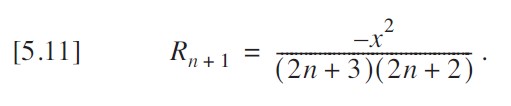
?改進版本消除了對 pow () 和 factorial () 的調用。此版本如下代碼所示。
double sine(double x){double last = x;double retval = x;double eps = 1.0e-16;long n = 1;do{n += 2;last *= (-x * x/((double)n * (double)(n-1)));retval += last;
}while((abs(last) > eps));return retval;
}?如上 中的代碼效率尚可,許多人可能想就此打住。然而,這個函數的實現方式仍然相當糟糕。我可以通過僅計算一次 x2 來稍作改進,但還有一種更好的方法 —— 方程 [5.11] 中的關系給出了線索:每一項都是下一項的一個因子。事實上,這甚至包括值 x,它存在于每一項中。因此,我可以將方程 [5.7] 和 [5.8] 因式分解為:

????????這種公式化方法被稱為霍納法則,它幾乎是計算該級數的最優方式。請注意,每一步的分母都是兩個連續整數的乘積 —— 在正弦級數中為 2×3、4×5、6×7,等等。一旦你發現這一規律,就能憑記憶寫出這些函數的計算式。如果無法使用現成的正弦函數,而你又急需一個,直接對這兩個方程進行編碼其實相當不錯。
????????不過仍有幾個細節需要解決。首先,我遇到一個小問題:由于必須保存所有中間結果,所示方法會占用大量棧空間。如果你的編譯器是高度優化的,或者你不介意棧空間消耗,這不會有問題。但如果你使用的是簡單編譯器和 80x87 數學協處理器,你會像我一樣很快發現,協處理器可能會發生棧溢出。
????????式5-12可以重新改寫為:
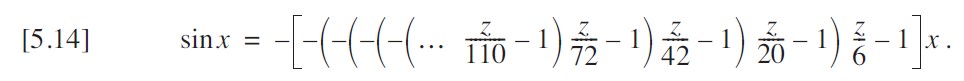
????????但對于計算機實現而言,我可以通過另一輪變換消除一半的符號變化。這可能并不明顯,但如果我仔細地將所有前導負號折疊到括號內的表達式中,就能得到等效的形式。
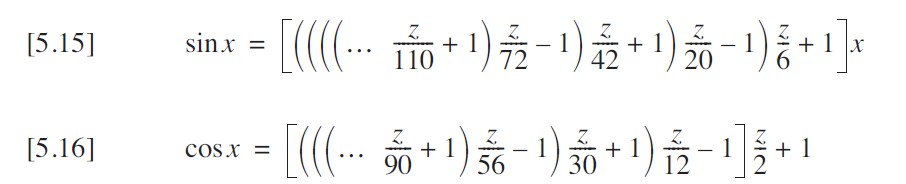
????????這已經是相當高效的實現方式了。這些方程雖然看起來不簡潔,但計算速度非常快。就像我可以在方程 [5.12] 和 [5.13] 的右側添加更多項一樣,也可以在方程 [5.15] 和 [5.16] 的左側添加項。只需記住,這次符號是交替變化的,從右端顯示的正號開始。
??????? 如下代碼展示了這些方程的直接實現。所使用的項數適用于 32 位浮點精度和 ±45° 的范圍。由于大多數計算機執行乘法的速度比除法快,我通過將常數存儲為其倒數來調整了算法(不用擔心涉及常數的表達式,大多數編譯器會對這些部分進行優化)。注意名稱前添加的下劃線,這是為了強調(雙關語)這些函數僅在有限范圍內有用的事實。我會在后面的全范圍版本中使用這些函數。
// Find the Sine of an Angle <= 45
double _sine(double x){double s1 = 1.0/(2.0*3.0);double s2 = 1.0/(4.0*5.0);double s3 = 1.0/(6.0*7.0);double s4 = 1.0/(8.0*9.0);double z = x * x;return ((((s4*z-1.0)*s3*z+1.0)*s2*z-1.0)*s1*z+1.0)*x;
}
// Find the Cosine of an Angle <= 45
double _cosine(double x){double c1 = 1.0/(1.0*2.0);double c2 = 1.0/(3.0*4.0);double c3 = 1.0/(5.0*6.0);double c4 = 1.0/(7.0*8.0);double z = x * x;return (((c4*z-1.0)*c3*z+1.0)*c2*z-1.0)*c1*z+1.0;
}?????????第二個細節?我悄悄省去了一個用于判斷使用多少項的測試。由于必須從內到外計算霍納法則,你必須知道 “內部” 從哪里開始。這意味著你不能在計算過程中測試各項;必須預先知道需要多少項。在這種情況下,對于小的 x 值,霍納法則的額外效率抵消了跳過內部項計算可能獲得的任何收益。這一結果與第 4 章中關于平方根的討論得出的結論相似:有時固定次數地計算某些內容會更簡單(而且通常更快),而不是測試某個終止條件。如果這能讓你更放心,可以為 x 非常接近零的特殊情況添加一個測試;否則,最好計算完整的表達式。
????????你可能想知道,既然我已經在方程 [5.5] 中表明余弦可以由正弦推導而來,為什么還要同時包含正弦和余弦函數。原因很簡單:即使你只對其中一個函數感興趣,實際上也需要能夠計算這兩個函數。當結果接近零時,一種近似最準確;當結果接近一時,另一種近似最準確。根據輸入值的不同,你最終會使用其中一種或另一種。
霍納法則的計算必須從內到外逐層展開,這意味著無法在循環中動態判斷項數,必須預先確定需要計算的項數。這一限制帶來兩個關鍵問題:
1. 為何放棄動態項數測試?
- 霍納法則的結構性限制:其嵌套乘法形式(如 sin(x)=x?(1?3!x2??(1?5×4x2??(?))))要求先計算最內層項,再向外逐層展開。若在計算中動態判斷是否終止(如 “當項值小于誤差閾值時停止”),需存儲所有中間層結果,這會抵消霍納法則的空間優化優勢。
- 小角度場景的效率平衡:對于小 x(如 x≈0),級數收斂極快,理論上只需 1-2 項即可滿足精度。但預定義固定項數(如 4 項)的計算成本可能低于動態測試的判斷開銷(如條件分支、浮點比較)。正如第 4 章平方根計算的結論:固定次數的計算有時比動態終止更高效。
為何同時實現正弦與余弦函數?
盡管余弦可通過正弦推導(cos(x)=sin(2π??x)),但獨立實現兩者仍有必要:
1. 精度互補性
- 正弦在 0 附近更精確:當 x≈0 時,正弦級數首項 x 直接逼近真實值,而余弦級數首項為 1,次項 ?2x2? 對小 x 的修正量極小,需更多項才能達到同等精度。
- 余弦在 2π? 附近更精確:當 x≈2π? 時,余弦值接近 0,其級數收斂更快;而正弦值接近 1,需更多項修正首項 x 的較大偏差。
2. 輸入范圍的動態選擇
- 根據輸入 x 的范圍選擇計算路徑:
- 若 x 靠近 kπ(正弦主導區間),優先計算正弦,再通過三角恒等式推導余弦。
- 若 x 靠近 kπ+2π?(余弦主導區間),直接計算余弦更高效。
- 避免大角度誤差累積:例如,計算 cos(179°) 時,若通過 sin(1°) 推導,需先將 179° 約簡為 1°,再調用正弦函數。此過程可能引入額外的約簡誤差,而直接計算余弦可避免中間步驟
????????至此,我已證明如果輸入參數的范圍可以限制,就能實現一個良好且高效的正弦函數。接下來需要說明的是,我確實可以限制范圍。

)
















)
