3342.到達最后一個房間的最少時間II

• 思路分析：最短路徑問題，當然，由于不同的格子之間的移動的代價不統一,所以這個最短路徑需要使用Dijkstra算法進行求解，對于直接使用Dijkstra算法模版的題目，大家可以先去做一下3341. 到達最后一個房間的最少時間 I
• 這個題目難點在于如何計算從格子(x,y)出發的代價是1還是2

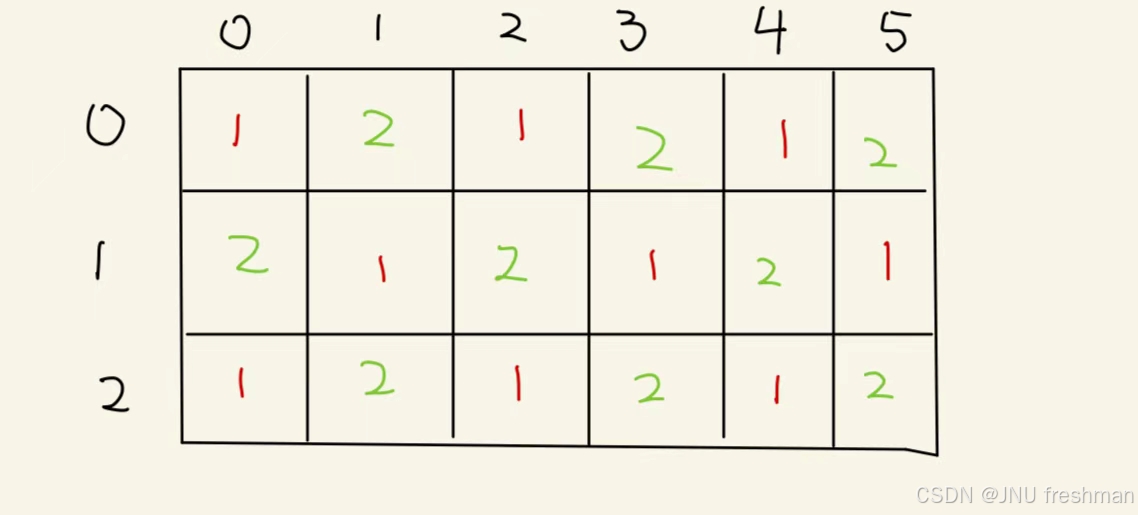
• 通過畫出具體的轉移代價的圖，我們發現是有規律的，當當前位于(x,y)的時候，轉移的代碼可以表示為(x+y)%2 + 1,既然得出了代價的計算，那么接下來直接套用Dijkstra算法的模版即可

import heapq
class Solution:def minTimeToReach(self, moveTime: List[List[int]]) -> int:n,m = len(moveTime),len(moveTime[0])dis = [[float("inf")]*m for _ in range(n)]dis[0][0] = 0 h = [(0,(0,0))]tmp = []cou = 1step = [(0,-1),(0,1),(-1,0),(1,0)]# 感覺得來一個中轉的while h:d,(x,y) = heapq.heappop(h)if d > dis[x][y]:continueif x == n-1 and y == m-1:return d # 訪問鄰居# 處理十分巧妙time = (x+y) % 2 + 1for dx,dy in step:nx,ny = x+dx,y+dy if 0<=nx<n and 0<=ny<m:newdis = d + time if d + time > moveTime[nx][ny] + time else moveTime[nx][ny] + timeif newdis < dis[nx][ny]:dis[nx][ny] = newdisheapq.heappush(h,(newdis,(nx,ny)))