隨機事件及其概率
加法公式
推三個的時候ABC，夾逼準則
減法準則
?
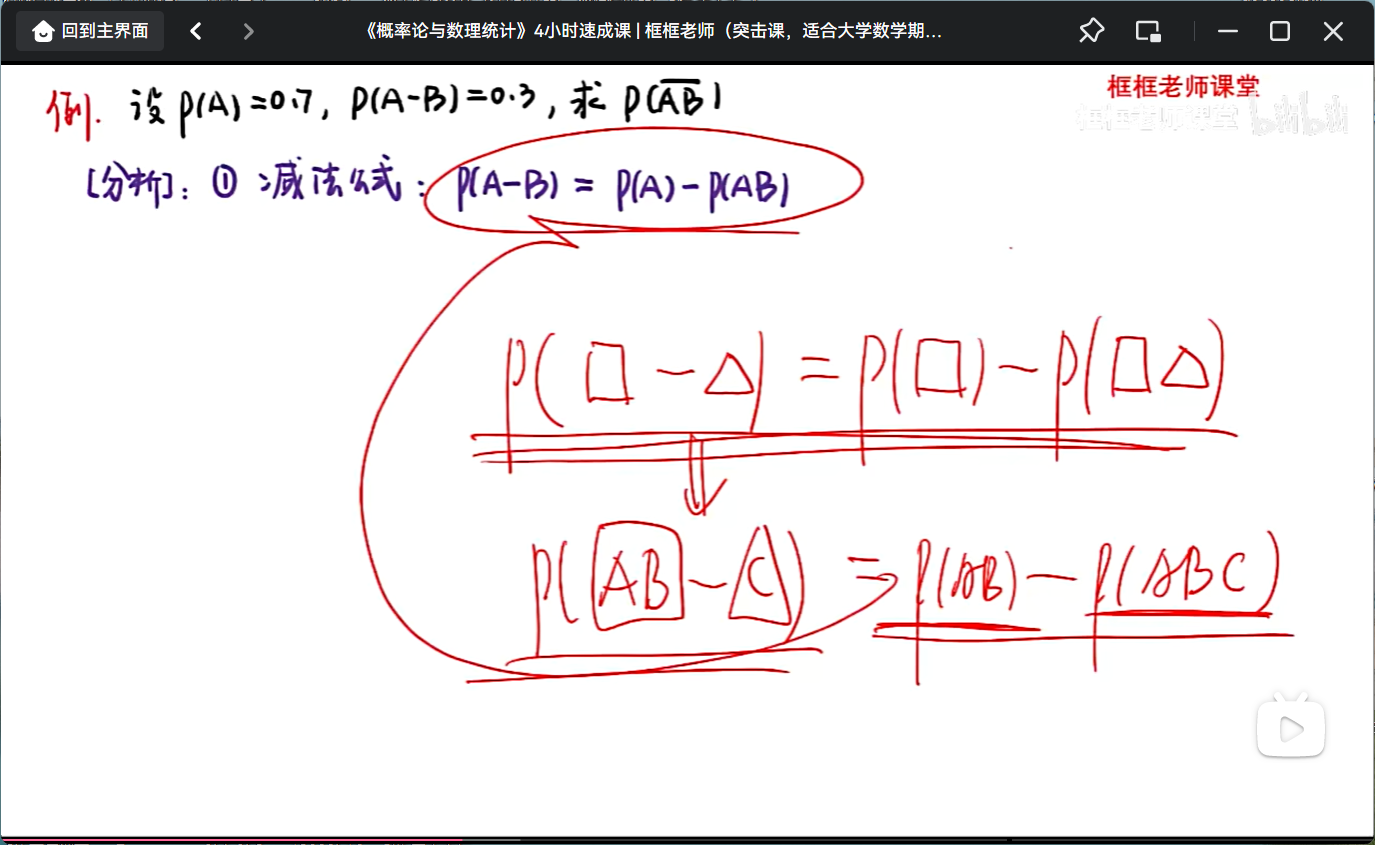
除法公式
相互獨立定義
兩種分析 兩個解法
古典概型求概率（排列組合）
分步相乘、分類相加
全概率公式和貝葉斯公式
兩階段問題
第一個小概率*A在小概率的概率。。。累計
分子*反過來/全概率
求誰把誰設為A
例題
看到：已知、條件下 用條件概率
確定A的條件下，求某一個小概率，用貝葉斯
求A 用全概率公式
伯努利概型
一維隨機變量及其分布
離散型求分布律（表格）
關乎順序用A
常見離散分布 求概率
如二項分布
連續性隨機變量（RV）相關計算
分布函數F（x）求導，得到密度f（x）
已知密度f（x），求區間概率P，定積分（導回去）。或者用分布函數區間前后減去
概率密度為相同值的情況下，可以合并條件為其他
例題
已知f求常數、F
求K——規范性
不定積分（導回去），別忘記常數
?
不定積分！！！別忘記常數了
三個任意常數的情況
密度f有其他的區域條件
——在分段點處連續——左極限=右極限
?
二、一維隨機變量
U均勻分布
求子區間的概率密度，用長度之比即可
N正態分布_標準化
標準化，使得呈現y軸對稱，括號右邊，越小越尖
N（0,1）標準正態分布，和y軸對稱
?
例題
求概率:1.畫圖即得到? 2.利用公式法，轉化為標準正態分布，因為要求P（x<0）,標準化，使得為
（-2），題目中2-4，標準化后為2，0，根據正反相加為1，即得相反數
離散型 函數分布
分布律——先求取值，再求概率
連續型函數分布（不懂）！！
y的函數兩個分段點，分三段來考慮；1個就分2段
分布函數定義：X隨機變量<x自變量
求出密度函數—代入所求函數，按照分段點，把x劃出來，定積分，求得區域分布函數
注意 分母不為0
二維隨機變量及其分布
二維離散型 分布
聯合分布律是表格，邊緣分布律行行列列相加
邊緣分布律
別把X Y搞混了
條件分布律
不可以直接在表格中摘出來，用符合的概率/在那個條件下的整體的概率（例如在Y=1的條件下，就要把Y=1的概率全部加起來）
獨立與否
看每行成不成比例
大題：聯合概率 不等于 邊緣概率的乘積——P（x,y）不等于P（x）*P（y）
二維 連續型！！必考最后一道
解題方法
求未知參數
已知f(x,y)，反求參數，用規范性——區域內的不定積分=1
注意函數區域D畫對，這樣積分上下限才是對的
二重積分：一個積分積完，結果直接代入到下一重積分內，化簡即得
根據密度函數的分布，畫出區域--得到積分上下限
求區域密度
在題目的基礎上的新的小區域
區域要寫成該題要求和題目的區域的交集，雙重積分，就把f（x，y）帶入再化開區域解
y的上下限，穿y——從下至上
求邊緣密度函數
給對方定積分，就會把對方消掉
求概率值不能代0，但是函數可以為0，所以別漏掉
求x的邊緣密度就豎著，y的就橫著，
積分上下限：y從下到上。x從左到右
邊緣密度的每一個區域都要重新求
條件密度=聯合密度/邊緣密度
獨立與否
邊緣密度相乘 不等于聯合密度
兩個離散型 函數 分布律
兩個連續函數 求密度函數（跳過一下）
假設檢驗
?
?
?
?
?
?
?
