名人說：路漫漫其修遠兮，吾將上下而求索。—— 屈原《離騷》
創作者：Code_流蘇(CSDN)（一個喜歡古詩詞和編程的Coder😊）
專欄：《Python星球日記》，限時特價訂閱中ing

目錄

• • 一、標量、向量、矩陣的基本概念
  • • 1. 標量
    • 2. 向量
    • 3. 矩陣
  • 二、矩陣運算
  • • 1. 矩陣加法
    • 2. 矩陣乘法
    • 3. 矩陣轉置
    • 4. 逆矩陣
  • 三、向量空間與線性組合
  • • 1. 向量空間的概念
    • 2. 線性組合
    • 3. 線性獨立性
  • 四、NumPy 實踐：矩陣運算
  • • 1. NumPy 基礎
    • 2. 使用 NumPy 進行矩陣運算
    • 3. 實戰示例：使用NumPy解線性方程組
  • 總結與展望

👋 專欄介紹： Python星球日記專欄介紹（持續更新ing）
? 上一篇： 《Python星球日記》第35天：全棧開發（綜合項目）

歡迎來到Python星球的第36天！🪐

在前面我們學習了Python基礎、爬蟲、數據可視化，并深入了解了Web開發。今天，我們將探索線性代數基礎，這是數據科學和機器學習領域的重要基石。無論是圖像處理、推薦系統還是神經網絡，線性代數都是不可或缺的數學工具。讓我們一起踏上這段數學之旅！

一、標量、向量、矩陣的基本概念

在線性代數中，我們首先需要理解三個基本概念：標量、向量和矩陣。這些是構建整個線性代數體系的基礎元素。

1. 標量

標量（Scalar）是最簡單的數學對象，它就是一個單獨的數字。

比如：5、-3、0.5、π 等都是標量。在Python中，我們可以用常規的數值類型來表示標量：

# 標量示例
a = 5       # 整數類型標量
b = 3.14    # 浮點類型標量
c = 2 + 3j  # 復數類型標量

2. 向量

向量（Vector）是有序的數字集合，可以看作是一個一維數組。向量可以表示為行向量（橫排）或列向量（豎排）。

在Python中，我們通常使用NumPy庫中的array或vector來表示向量：

import numpy as np# 創建向量
column_vector = np.array([[1], [2], [3]])  # 列向量 - 形狀為(3,1)
row_vector = np.array([4, 5, 6])           # 行向量 - 形狀為(3,)print(column_vector)
print(row_vector)

向量可以表示空間中的方向和大小，如位置、速度或力，也可以表示數據集中的特征集合。

3. 矩陣

矩陣（Matrix）是二維數字表格，可以看作是向量的集合。矩陣由行和列組成，通常用大寫字母表示（如A、B等）。

矩陣的維度由其行數和列數決定。一個有m行n列的矩陣稱為m×n矩陣。

在Python中，使用NumPy創建矩陣非常簡單：

import numpy as np# 創建2×3矩陣
A = np.array([[1, 2, 3],[4, 5, 6]])print(A)
print(f"矩陣維度: {A.shape}")  # 輸出: (2, 3)

矩陣在數據科學和機器學習中應用廣泛，例如：

• 圖像處理中的圖像就是像素矩陣
• 社交網絡中的連接關系可用鄰接矩陣表示
• 推薦系統中的用戶-物品評分矩陣

二、矩陣運算

矩陣的基本運算包括加法、乘法、轉置和求逆。讓我們逐一了解這些操作并用NumPy實現。

1. 矩陣加法

矩陣加法的規則很簡單：相同位置的元素相加。兩個矩陣必須具有相同的維度才能相加。

NumPy實現矩陣加法非常直觀：

import numpy as np# 創建兩個2×2矩陣
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])# 矩陣加法
C = A + Bprint(f"矩陣A:\n{A}")
print(f"矩陣B:\n{B}")
print(f"A + B =\n{C}")  # 輸出: [[6 8], [10 12]]

矩陣加法滿足交換律和結合律：A + B = B + A 以及 (A + B) + C = A + (B + C)。

2. 矩陣乘法

矩陣乘法比加法復雜，有兩種主要類型：

• 點乘（element-wise multiplication）：對應位置的元素相乘
• 矩陣乘法（matrix multiplication）：遵循特定的數學規則

矩陣乘法要求第一個矩陣的列數等于第二個矩陣的行數。假設矩陣A的維度是m×n，矩陣B的維度是n×p，那么A×B的結果是一個m×p的矩陣。

NumPy中實現矩陣乘法有多種方式：

import numpy as np# 創建矩陣
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])# 點乘（元素相乘）
C_elementwise = A * B
print(f"點乘結果:\n{C_elementwise}")  # 輸出: [[5 12], [21 32]]# 矩陣乘法
C_matmul = np.matmul(A, B)  # 或使用 A @ B (Python 3.5+)
print(f"矩陣乘法結果:\n{C_matmul}")  # 輸出: [[19 22], [43 50]]# 使用 dot 函數
C_dot = A.dot(B)
print(f"使用dot函數的結果:\n{C_dot}")  # 輸出與C_matmul相同

矩陣乘法不滿足交換律：通常情況下，A×B ≠ B×A。這是初學者容易犯的一個錯誤。

3. 矩陣轉置

矩陣的轉置是指將矩陣的行和列互換。如果A是一個m×n矩陣，那么它的轉置A^T是一個n×m矩陣。

在NumPy中，轉置操作非常簡單：

import numpy as np# 創建2×3矩陣
A = np.array([[1, 2, 3],[4, 5, 6]])# 轉置矩陣
A_T = A.T  # 或使用 np.transpose(A)print(f"原矩陣A:\n{A}")
print(f"轉置后A^T:\n{A_T}")

矩陣轉置的一些重要性質：

• (A^T)T = A（轉置的轉置等于原矩陣）
• (A + B)^T = A^T + B^T（轉置分配律）
• (AB)^T = B^T A^T（轉置的乘法順序會反轉）

4. 逆矩陣

逆矩陣是線性代數中的一個重要概念。只有方陣（行數等于列數的矩陣）才可能有逆矩陣。

如果矩陣A的逆矩陣存在，記為A^(-1)，則有：A × A^(-1) = A^(-1) × A = I，其中I是單位矩陣（對角線上元素為1，其他元素為0）。

在NumPy中，可以使用np.linalg.inv()函數求矩陣的逆：

import numpy as np# 創建可逆矩陣
A = np.array([[4, 7], [2, 6]])# 計算逆矩陣
try:A_inv = np.linalg.inv(A)print(f"矩陣A:\n{A}")print(f"A的逆矩陣:\n{A_inv}")# 驗證 A × A^(-1) = II = np.dot(A, A_inv)print(f"A × A^(-1) =\n{np.round(I, decimals=10)}")  # 使用round處理浮點誤差
except np.linalg.LinAlgError:print("矩陣不可逆")

需要注意的是，并非所有矩陣都有逆矩陣。如果矩陣的行列式為0，那么它沒有逆矩陣，被稱為奇異矩陣或不可逆矩陣。

逆矩陣在解線性方程組和機器學習中非常重要，比如在線性回歸中求解系數時就需要用到。

三、向量空間與線性組合

1. 向量空間的概念

向量空間是包含向量的集合，該集合對向量加法和標量乘法運算封閉。簡單來說，向量空間是一組向量，且任意兩個向量的和以及任意向量與標量的積仍然屬于該空間。

最常見的向量空間是歐幾里得空間，如二維平面R2或三維空間R3。

2. 線性組合

線性組合是向量空間的一個核心概念。一組向量的線性組合是指將這些向量乘以標量系數后相加。

形式上，向量v?, v?, …, v?的線性組合可表示為：c?v? + c?v? + … + c?v?

其中c?, c?, …, c?是標量系數。

通過線性組合，我們可以用少量的基礎向量生成整個向量空間。例如，在二維空間中，任何向量都可以表示為標準基向量i = [1, 0]和j = [0, 1]的線性組合。

import numpy as np
import matplotlib.pyplot as plt# 設置中文字體支持
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 標準基向量
e1 = np.array([1, 0])  # i 向量
e2 = np.array([0, 1])  # j 向量# 任意向量作為線性組合
v = np.array([3, 2])   # 3i + 2j# 可視化
plt.figure(figsize=(8, 6))
plt.axhline(y=0, color='k', linestyle='-', alpha=0.3)
plt.axvline(x=0, color='k', linestyle='-', alpha=0.3)
plt.arrow(0, 0, e1[0], e1[1], head_width=0.1, head_length=0.1, fc='blue', ec='blue', label='e1')
plt.arrow(0, 0, e2[0], e2[1], head_width=0.1, head_length=0.1, fc='green', ec='green', label='e2')
plt.arrow(0, 0, v[0], v[1], head_width=0.1, head_length=0.1, fc='red', ec='red', label='v=3e1+2e2')
plt.grid(True, alpha=0.3)
plt.xlim(-0.5, 4)
plt.ylim(-0.5, 3)
plt.legend()
plt.title('向量的線性組合示例')
plt.show()

3. 線性獨立性

向量集合{v?, v?, …, v?}如果滿足：c?v? + c?v? + … + c?v? = 0只有當所有c? = c? = … = c? = 0時成立，那么這組向量就是線性獨立的。

換句話說，線性獨立意味著集合中的任何向量都不能表示為其他向量的線性組合。

在NumPy中，我們可以用以下方法檢查向量是否線性獨立，通常通過計算矩陣的秩（rank）：

import numpy as np# 創建向量集合
v1 = np.array([1, 0, 0])
v2 = np.array([0, 1, 0])
v3 = np.array([1, 1, 0])  # v3 = v1 + v2，所以是線性相關的# 將向量作為矩陣的行
matrix = np.vstack((v1, v2, v3))# 計算矩陣的秩
rank = np.linalg.matrix_rank(matrix)# 判斷線性獨立性
n_vectors = matrix.shape[0]  # 向量數量
if rank == n_vectors:print("這些向量是線性獨立的")
else:print("這些向量是線性相關的")print(f"秩 = {rank}，向量數量 = {n_vectors}")

線性獨立性的概念在許多領域都很重要：

• 在機器學習中，特征選擇就是要找到線性獨立的特征集合
• 在主成分分析（PCA）中，我們尋找數據的主成分，這些主成分是線性獨立的
• 在解線性方程組時，判斷方程組是否有唯一解

四、NumPy 實踐：矩陣運算

現在讓我們通過一系列實際的Python代碼示例，鞏固對線性代數的理解。

1. NumPy 基礎

NumPy是Python中進行科學計算的基礎庫，提供了強大的多維數組對象和處理這些數組的工具。

import numpy as np# 創建數組
a = np.array([1, 2, 3])                # 一維數組
b = np.array([[1, 2, 3], [4, 5, 6]])   # 二維數組# 一些基本操作
print(f"數組b的形狀: {b.shape}")        # (2, 3)
print(f"數組b的維度: {b.ndim}")         # 2
print(f"數組b的元素類型: {b.dtype}")    # int64
print(f"數組b的元素總數: {b.size}")     # 6# 創建特殊矩陣
eye = np.eye(3)                        # 3×3單位矩陣
zeros = np.zeros((2, 3))               # 2×3全零矩陣
ones = np.ones((2, 2))                 # 2×2全一矩陣
random_matrix = np.random.rand(2, 3)    # 2×3隨機矩陣print(f"單位矩陣:\n{eye}")

2. 使用 NumPy 進行矩陣運算

讓我們實現前面討論過的矩陣運算：

import numpy as np# 創建樣例矩陣
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])# 1. 矩陣加法
C_add = A + B
print(f"矩陣加法 A + B =\n{C_add}")# 2. 矩陣乘法
C_mul = A @ B  # 或 np.matmul(A, B) 或 A.dot(B)
print(f"矩陣乘法 A × B =\n{C_mul}")# 3. 矩陣轉置
A_T = A.T
print(f"矩陣A的轉置 =\n{A_T}")# 4. 矩陣的逆（如果存在）
try:A_inv = np.linalg.inv(A)print(f"矩陣A的逆 =\n{A_inv}")# 驗證 A × A^(-1) = II_check = A @ A_invprint(f"A × A^(-1) =\n{np.round(I_check, decimals=10)}")
except np.linalg.LinAlgError as e:print(f"錯誤: {e}")# 5. 求矩陣的行列式
det_A = np.linalg.det(A)
print(f"矩陣A的行列式 = {det_A}")# 6. 求矩陣的特征值和特征向量
eigenvalues, eigenvectors = np.linalg.eig(A)
print(f"矩陣A的特征值 = {eigenvalues}")
print(f"矩陣A的特征向量 =\n{eigenvectors}")

3. 實戰示例：使用NumPy解線性方程組

線性代數的一個重要應用是解線性方程組。例如，解方程組：

• 2x + y = 8
• 3x + 5y = 19

可以表示為矩陣形式：AX = B，其中A是系數矩陣，X是未知數向量，B是常數向量。

import numpy as np# 定義系數矩陣A和常數向量B
A = np.array([[2, 1], [3, 5]])
B = np.array([8, 19])# 方法1：使用矩陣的逆
# X = A^(-1) × B
X1 = np.linalg.inv(A).dot(B)
print(f"使用矩陣的逆解得: x = {X1[0]}, y = {X1[1]}")# 方法2：使用numpy的線性代數解法函數
X2 = np.linalg.solve(A, B)
print(f"使用linalg.solve解得: x = {X2[0]}, y = {X2[1]}")# 驗證解是否正確
verification = A @ X2
print(f"驗證: A × X = {verification}，應等于B = {B}")

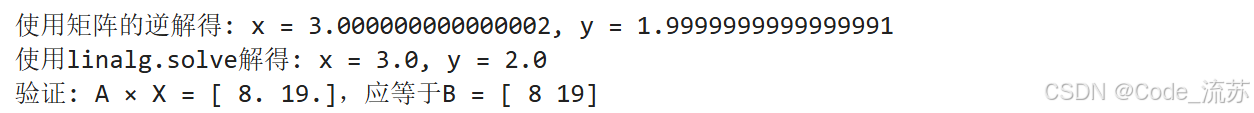
這個例子展示了如何將實際問題轉化為線性代數問題并使用NumPy求解。這種方法在數據科學、機器學習和科學計算中應用廣泛。

總結與展望

今天，我們學習了線性代數的基礎知識，包括標量、向量和矩陣的概念，矩陣的基本運算（加法、乘法、轉置和求逆），以及向量空間和線性組合的概念。我們還通過NumPy實現了這些操作，并展示了如何應用線性代數解決實際問題。

線性代數是機器學習和數據科學的重要基礎。在未來的學習中，你會發現這些知識對于理解以下內容至關重要：

• 機器學習算法，如線性回歸、主成分分析（PCA）和支持向量機（SVM）
• 深度學習中的矩陣運算和梯度下降
• 計算機圖形學中的變換矩陣
• 優化問題的數學建模和求解

下一步，你可以深入學習更多線性代數概念，以及它們在實際應用中的角色。

今天的知識是我們探索數據科學和人工智能宇宙的第一步，未來我們將繼續這段Python星球探索之旅！

---

通過這篇文章，你已經掌握了線性代數的基礎知識和NumPy的矩陣操作。試著自己實現一些示例，加深對概念的理解。線性代數不僅僅是抽象的數學，它是解決現實問題的強大工具！

創作者：Code_流蘇(CSDN)（一個喜歡古詩詞和編程的Coder😊）
如果你對今天的內容有任何問題，或者想分享你的學習心得，歡迎在評論區留言討論！