題目背景
跳臺滑雪起源于 19 世紀,是冬季運動會的傳統競技項目。今年亞洲冬季運動會在我國
哈爾濱舉行,跳臺滑雪項目吸引了包括中國在內的亞洲各國運動健兒踴躍參加,我國運動員取得了優異的成績。
跳臺滑雪融合了速度、力量與精確控制,展現出運動員在高空飛躍中的技巧與勇氣,是冬季運動中最具觀賞性的項目之一。運動員在完成過程中,不同的身體姿態對最終得分有很大影響,分析各階段運動員應采取怎樣的姿態能夠提高運動成績。
跳臺滑雪的比賽場地通常由出發臺、助滑坡、起跳臺、著陸坡和終止區組成,如下圖所示。跳臺滑雪的技術可分解為助滑與起跳、空中飛行、著陸和終止滑行 4 個階段。
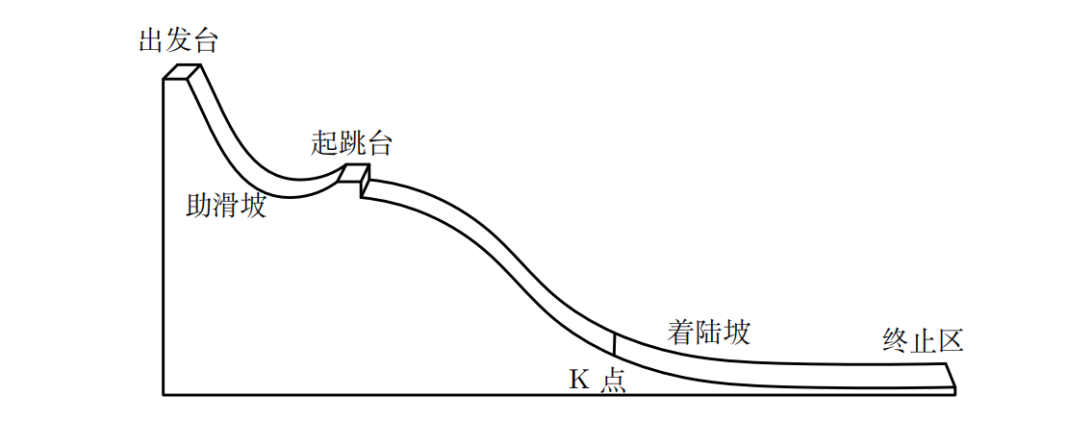
跳臺滑雪的評分標準由距離分和姿勢分組成,并結合賽道參數計算總分(附錄 A)。
請建立數學模型,解決以下問題,并根據附錄 B 提供的賽道數據給出計算結果。
解題摘要
針對問題一,我們建立了助滑階段空氣動力學模型。考慮到滑行過程中的空氣阻力和摩擦力對速度的影響,我們引入了不同姿態下運動員迎風面積和空氣阻力系數的變化,利用牛頓第二定律建立加速度表達式,并通過數值模擬比較常見姿態下的終端速度。結果表明,運動員應采取低蹲前傾姿勢,以降低迎風面積和阻力系數,從而獲得最大的起跳速度。
針對問題二,我們構建了二維空中飛行動力學模型,結合起跳速度、身體迎角、滑雪板傾角等因素,模擬運動員在空中飛行的軌跡與姿態變化,采用歐拉法對運動過程進行仿真,優化飛行路徑和穩定性。仿真結果表明,運動員應在起跳后保持滑雪板與身體成“V”字形打開、重心略后傾的姿態,以增強升力、延長飛行距離并提高姿態得分。
針對問題三,我們基于力學平衡條件建立了著陸平衡模型,引入重心位置、著陸角度、風速與反應延遲等變量構建穩定性評分函數,并使用Python對著陸過程進行熱力圖仿真。結果顯示,運動員在著陸時應保持重心盡量居中、著陸角接近坡面角度(約34°),并提前調節姿態以補償神經反應延遲,以實現最佳平衡狀態并避免扣分。
問題一
?運動員在助滑坡應采取何種姿勢,以獲得較大的起跳速度?
我們可以為跳臺滑雪的全過程建立一個完整的三階段數學模型(助滑 + 飛行 + 著陸),并模擬出跳躍的軌跡和最終得分。
階段一:助滑 + 起跳
模擬從高處加速下滑過程,計算到達起跳臺末端的速度。
起跳點速度作為飛行初速度輸入。
階段二:空中飛行
建立包含重力和空氣動力的二維運動模型(含升力和阻力)。
模擬運動員在空中軌跡,計算水平飛行距離。
階段三:著陸判定與得分
根據飛行距離判斷是否落在 K 點前/后。
計算距離分、姿勢分(設定規則或模擬不同落地情況)、風速補償(設為固定值或函數)。
輸出總得分。
所需參數設置(參考附錄 B 和物理常數)
| 參數 | 數值 | 說明 |
| 重力加速度 ggg | 9.81 m/s2 | 常數 |
| 空氣密度 ρ\rhoρ | 1.225 kg/m3 | 海平面 |
| 阻力系數 CD | 0.4(助滑)/ 0.6(飛行) | 姿勢相關 |
| 升力系數 CL | 0.3–0.6(飛行) | 滑雪板迎角決定 |
| 迎風面積 AAA | 0.4–0.6 m2 | 姿勢緊縮與否 |
| 運動員質量 mmm | 70 kg | |
| 助滑坡傾角 θ1\theta_1θ1? | 35° | 自定義或參考賽道圖 |
| 起跳角度 θ2\theta_2θ2? | 11° | 范圍10°–12° |
| 飛行起跳點高度 h0h_0h0? | 60 m | 落差約60米 |
| 起跳到著陸坡水平距離 | 140 m | |
| K 點位置 | 120 m |
代碼如下
#完整↓
#關zhu:數模Lab
#回復1
)


李宏毅)



)






)
---java版)



