題目介紹

鏈接: 611. 有效三角形的個數

思路分析

如果判斷三個數能否構成一個三角形，相信大家都知道：

只要任意兩邊之和大于第三邊即可。
比如三條邊長度為a，b，c
那只要滿足
a+b>c
a+c>b
b+c>a

但是，這樣要判斷三個條件，我們來介紹另一種方法：

如果三條邊的長短已經知道：a<=b<=c
那么此時只需滿足較短的兩條邊之和大于最長的那條邊，即
a+b>c
那么它們就一定能構成一個三角形，另外兩個條件就不需要判斷了
原理很簡單，因為c是最大的，c+一個數一定比另外兩條邊還大。

那題目呢，是給定一個包含非負整數的數組 nums ，要返回其中可以組成三角形三條邊的三元組個數。

所以，判斷的時候，我們可以先給數組排個序（升序）

然后呢，我們就可以用雙指針來解決這道題，具體怎么做呢？我們來看一個例子：

給這樣一個數組

最大值是10，所以我們先讓固定c為10
那a，b呢？

一個指向剩余區間的最大值，一個指向最小值
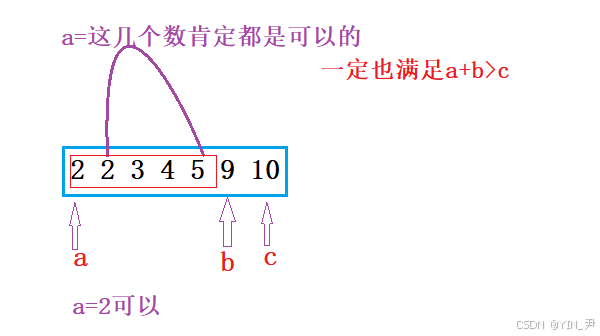
然后判斷，此時的a+b=11，當然大于10（第一種情況：a+b>c），所以當前這一組是滿足的，可以構成三角形。
然后我們觀察，此時a是最小的，所以此時ab之間的數據都是>=a的，所以中間的這些數據和b相加一定都大于此時的c。

一共種呢，就是b的下標-c的下標

當前情況下就是5-0=5種。
所以中間的情況就不用判斷了。b=9時一共5種情況可行。
假設兩個指針left和right分別指向ab，那接下來只需讓right--即可，判斷c=10，b=5時候的情況

此時a+b<c（第二種情況：a+b<=c）
所以構不成三角形，并且，可以斷定此時a和ab之間的數都相加都不大于c，因為這些數都比此時的b（5）小

所以固定c為10的情況下，a=2時，跟2 3 4 5都不行（9已經判斷過了）
所以此時讓left++，看后面的行不行（后面的數一定>=2，因為已經排序）
后序也是如此進行判斷。
這一輪結束后（當left>=right結束），固定c為10的情況就計算完了，只需讓c指向9，right從c的前面開始，left還從0下標開始，進重復上述操作，行下一輪的判斷即可。

總結一下：

1. 先固定c為最大的數
2. 定義雙指針，按照上述邏輯，判斷出當前情況下符合條件的三元組個數。
   如果a+b>c，b前面的元素個數就是b為當前值的情況下符合條件的三元組個數，然后b往前移（right- -）；
   如果a+b<=c，說明a為當前值的情況下找不到滿足條件的，讓a往后移（left++），再重新判斷
3. 固定c為次大的數，重復上述操作，當c前面的數小于2個，就結束了（即c的下標<2）

AC代碼

class Solution {
public:int triangleNumber(vector<int>& nums) {sort(nums.begin(),nums.end());int index_c=nums.size()-1;//c的下標int count=0;while(index_c>=2)//index_c<2，此時左邊的數就不夠兩個了{int left=0;//標識a的位置int right=index_c-1;//b的位置while(left<right){if((nums[left]+nums[right])>nums[index_c])      {count+=(right-left);--right;}else++left;}--index_c;}return count;}
};