前面我們講述了冒泡排序和選擇排序，我們本章講的排序方法是插入排序，插入排序是希爾排序實現的基礎函數，大家一定要好好理解插入排序的邏輯，這樣才能在后面學習希爾排序的時候，更容易的去理解，我們直接開始。

目錄

插入排序（以升序為例）

基本思想：

思路

代碼實現：

總結

希爾排序

基本思想：

一組一組依次排序代碼實現

多組同時排序

希爾排序的時間復雜度分析

總結

總結

---

插入排序（以升序為例）

基本思想：

直接插入排序是一種簡單的插入排序法，其基本思想是：
把待排序的記錄按其關鍵碼值的大小逐個插入到一個已經排好序的有序序列中，直到所有的記錄插入完為止，得到一個新的有序序列 。

就和我們打牌時，從小到大排牌序，當拿到一張新牌時，我們從后往前找，當最后的牌大于此時的牌，那么就讓最后一張牌向后挪動一位，繼續和倒數第二張比較，若倒數第二張小于此時的牌，就說明找到了位置，將此時的牌插入即可。

如上圖中，此時的牌為7，那么我們從后往前找，發現10>7,那么10就往后挪動，繼續向前找，發現是5，而5<7,說明找到了合適的位置將7放入5的后面即完成了插入排序。

思路

當插入第i(i>=1)個元素時，前面的array[0],array[1],…,array[i-1]已經排好序，此時用array[i]的排序碼與array[i-1],array[i-2],…的排序碼順序進行比較，找到插入位置即將array[i]插入，原來位置上的元素順序后移

由于插入排序插入第i個元素時，需要前i-1個元素都是有序的，因此我們仍然需要從第1個元素開始排序

假設我們目前前i個是有序的，我們排序的就是第i+1個元素，我們用tmp記錄a[i+1]的值，然后從后往前開始依次比較，由下標i到下標0，我們再創建循環，用變量(j=i ， j >= 0 , j - -)控制循環

當 a[j] > tmp時，a[j]就向后挪動，即a[j+1] = a[ j ]??

當a[j] < tmp 時，說明已經找到了合適的位置，直接跳出循環，并將j+1的位置賦值為tmp即可

以下便是邏輯圖：?

以上是找到比tmp小正常插入的情況 ，還有一種情況，當數組在tmp前內沒有比tmp小的元素時，那么就會將小數放到數組首位，邏輯圖如下，還是上面數組的例子。

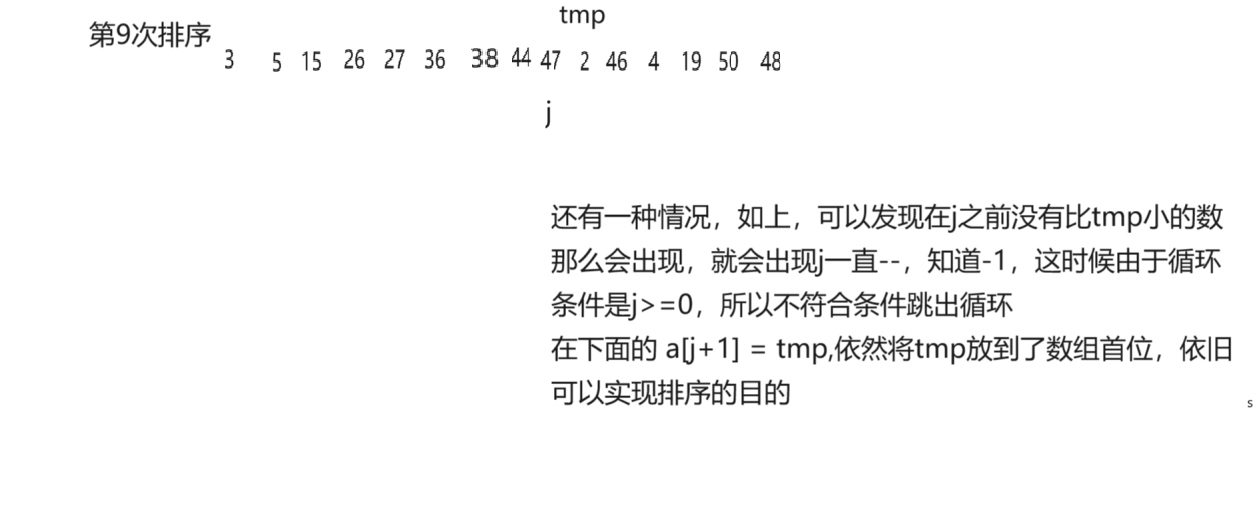
動態邏輯圖

代碼實現：

void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int tmp = a[i+1];int j = 0;for (j = i; j >= 0; j--){if (a[j] > tmp){a[j + 1] = a[j];}else{break;}}a[j+1] = tmp;}
}

小結

直接插入排序的特性總結：
1. 元素集合越接近有序，直接插入排序算法的時間效率越高
2. 時間復雜度：O(N^2)
3. 空間復雜度：O(1)，它是一種穩定的排序算法
4. 穩定性：穩定

希爾排序

希爾排序法又稱縮小增量法。希爾排序已經算是是排序中的大哥了，所以也比較難以理解，他是與快速排序，堆排序，歸并排序在同一條賽道上的排序算法，十分的厲害。

基本思想：

希爾排序法的基本思想是：先選定一個整數，把待排序文件中所有記錄分成個組，所有距離為的記錄分在同一組內，并對每一組內的記錄進行排序。然后，取，重復上述分組和排序的工作。當到達=1時，所有記錄在統一組內排好序。

可能比較難理解，希爾排序分為兩個部分，首先進行預排序，再進行插入排序

預排序：跨元素進行分組排序，讓數組更接近有序，這樣再進行插入排序的時候，基本都是在有序的情況下，那么再進行插入排序就減少了數組挪動的次數，效率更高了。

我們假設跳的距離為gap，gap初始值為3

看一下邏輯圖，我們就明白進行預排序后的效果

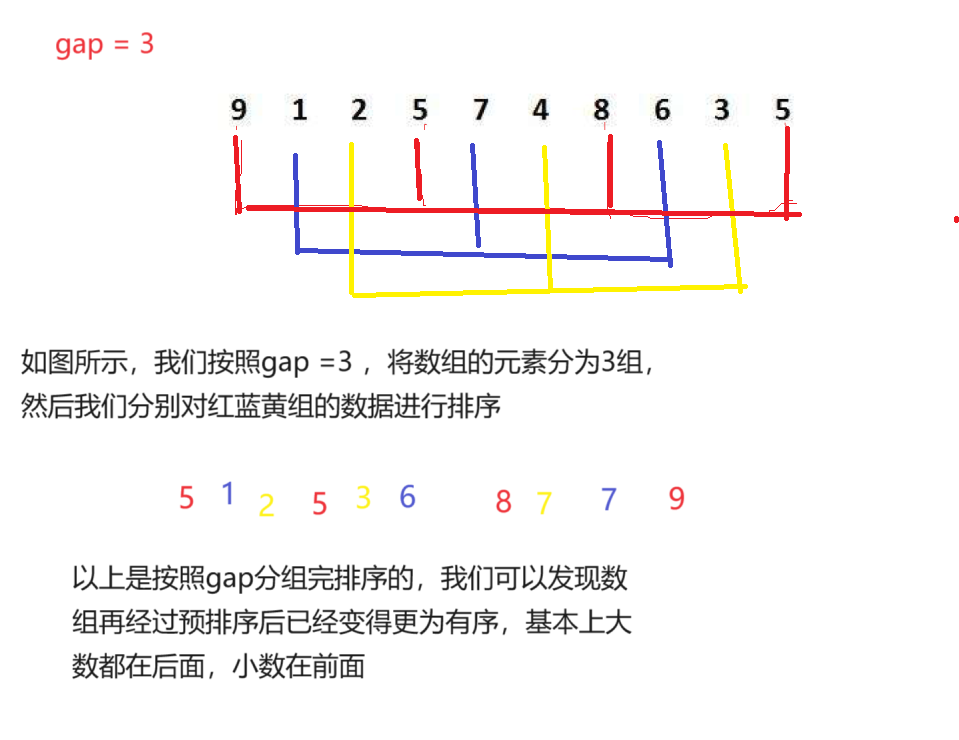
下面我們來單獨實現代碼，我們可以將代碼拆分成幾個小部分，依次實現，這樣會讓代碼實現變得更加容易實現，這便是由小及大的思想

我們先來實現對單個分組排序的實現，即對紅色排序的實現

代碼實現的底層邏輯，依然是插入排序，只不過在進行遍歷和比較的時候是一次跳躍gap個元素

大家看一下代碼實現應該就能理解

部分代碼實現

int gap = 3;
for (size_t i = 0; i < n - gap; i+=gap)
{int tmp = a[i + gap];int j = 0;for (j = i; j >= 0; j-= gap){if (a[j] > tmp){a[j + 1] = a[j];}else{break;}}a[j + gap] = tmp;
}

在完成單趟邏輯后，然后我們再建一個for循環，讓gap組依次進行排序，即完成了一組一組依次排序的邏輯實現

一組一組依次排序代碼實現

	int gap = 3;for (int k = 0; k < gap; k++){for (size_t i = k; i < n - gap; i += gap){int tmp = a[i + gap];int j = 0;for (j = i; j >= 0; j -= gap){if (a[j] > tmp){a[j + 1] = a[j];}else{break;}}a[j + gap] = tmp;}}

還有一種實現方法，是令多組同時進行排序，只需要修改一下邏輯代碼即可

多組同時排序

int gap = 3;
for (size_t i = 0 ; i < n - gap; i++)
{int tmp = a[i + gap];int j = 0;for (j = i; j >= 0; j -= gap){if (a[j] > tmp){a[j + 1] = a[j];}else{break;}}a[j + gap] = tmp;
}

二者的邏輯圖如圖所示

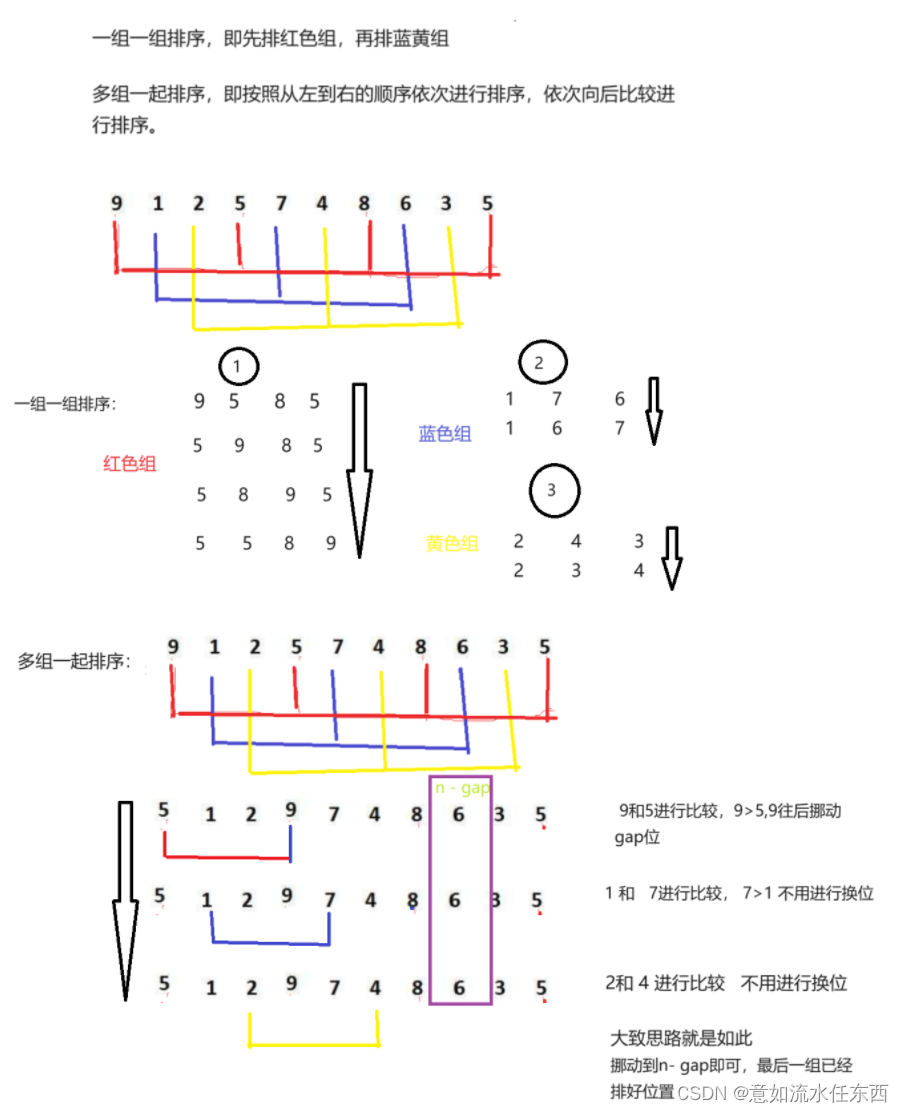
希爾排序的時間復雜度分析

希爾排序的時間復雜度比較難計算，因為gap的取值方法很多，導致很難去計算

我們通過上面的邏輯分析，發現 在預排序階段

gap越大，大的數可以更快的跳到后面，小的數可以更快的跳到前面，越不接近有序

gap越小，大的數跳到后面越慢，小的數跳到前面越慢，但越接近有序

因此控制gap的大小是增加效率的直接辦法

但是如何取最適合的gap呢，根據大量數據統計，我們發現當gap = n/3時效率最高，但是我們需要+1，保證gap最后等于1

代碼如下

void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){// +1保證最后一個gap一定是1// gap > 1時是預排序// gap == 1時是插入排序gap = gap / 3 + 1;for (size_t i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}

我們以n/3為例，以gap對時間復雜度的影響進行分析

如下

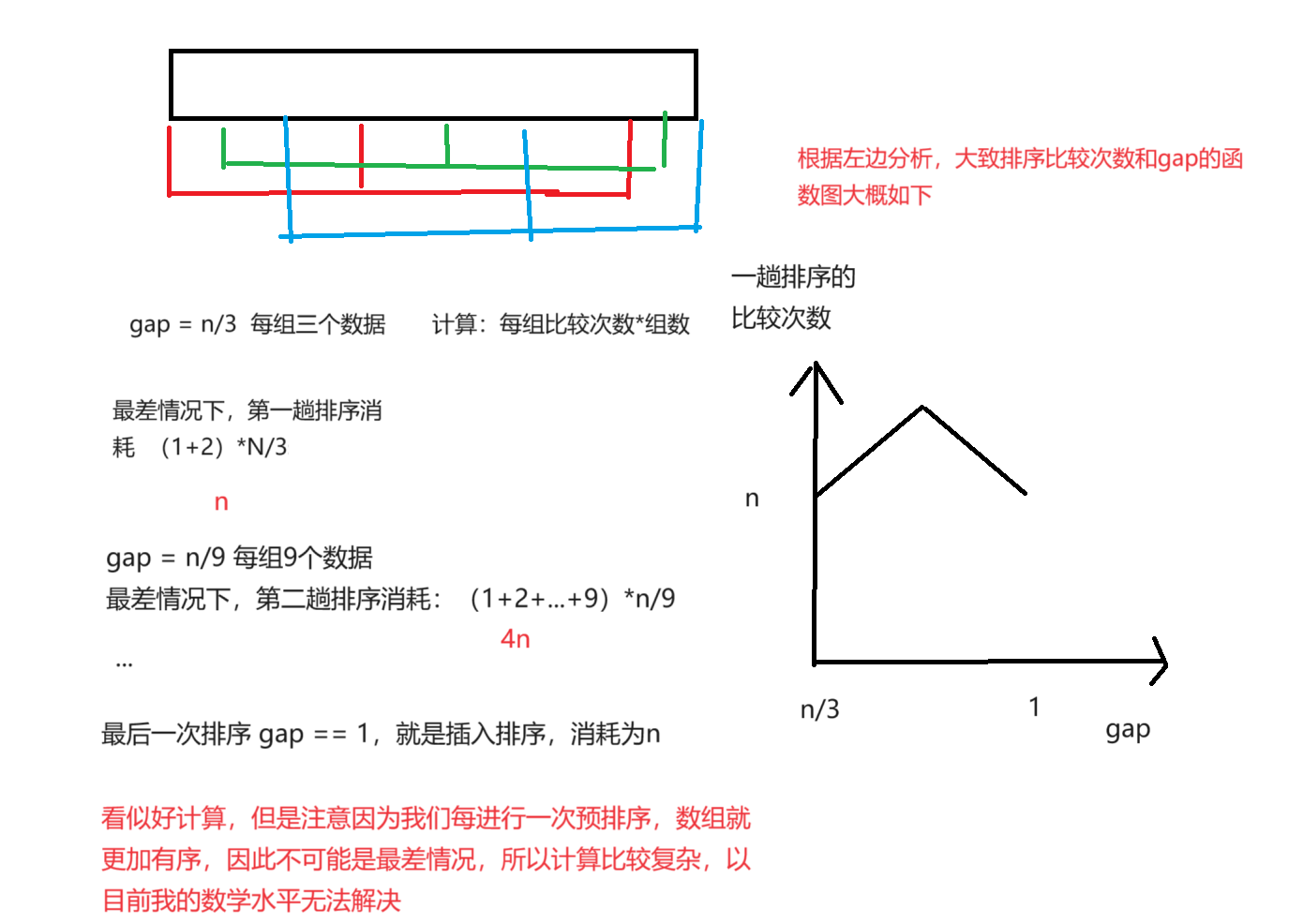
?代碼實現

void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){// +1保證最后一個gap一定是1// gap > 1時是預排序// gap == 1時是插入排序gap = gap / 3 + 1;for (size_t i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}

小結

1. 希爾排序是對直接插入排序的優化。

2. 當gap > 1時都是預排序，目的是讓數組更接近于有序。當gap == 1時，數組已經接近有序的了，這樣就會很快。這樣整體而言，可以達到優化的效果。我們實現后可以進行性能測試的對比。

3. 希爾排序的時間復雜度不好計算，因為gap的取值方法很多，導致很難去計算，因此在好些樹中給出的希爾排序的時間復雜度都不固定，通過數據統計，希爾排序的時間復雜度大概為O(n^1.3)

4. 穩定性：不穩定

總結

以上是對插入排序和希爾排序的分析，是一種新的排序思想，其中的種種知識點也很碎很多，希望大家能夠有所收獲。