---

前言

在先前的學習旅程中，我們探索了程序設計的基礎磚石——順序結構與分支結構。現在，我們踏上了新征途，深入循環結構的奧秘境地。循環，那是一種魔法，讓指令序列在滿足條件時重復施展，直至咒語終止。就像《西游記》里的奔波兒灞與灞波兒奔，兩者相輔相成對，相似又各異，循環結構中的for與while亦是如此，既有共通點，又各自獨異處。

循環結構，特別是for循環，如同編程中的時間輪回，讓代碼在特定條件下周而復現，賦予程序無限可能。我們從語法差異、應用場景、控制機制到選擇考量，全方位剖析for與while的同與別，助你在編程征途中，握選得宜劍。

學習路線：C++從入門到NOI學習路線

學習大綱：C++全國青少年信息學奧林匹克競賽（NOI）入門級-大綱

---

一、for循環

1.導入

在上一節中，我們講解了循環結構和while循環。相信大家通過一系列的題目練習對while循環已經掌握的爐火純青

那今天我們就要學習一種新的循環結構———for循環。

for循環和while循環有什么區別嗎？

它倆的區別就像是奔波兒灞，灞波兒奔。

既有相同之處又有不同之處。

我們將從以下幾點來對比兩個循環結構。

2.語法

首先從語法上比較，相同之處。

while循環和for循環都有初始化、條件表達式、迭代表達式。

• 初始化：在循環開始之前執行一次，通常用于設置循環控制變量。
• 條件表達式：在每次循環迭代前檢查，如果結果為真（非零），則執行循環體；如果為假（零），則循環結束。
• 迭代表達式：在每次循環體執行完畢后執行，通常用于更新循環控制變量。

不同的地方在哪里呢？

它們擺放的位置不一樣！！！

while循環的括號里只有條件判斷部分，初始化和迭代更新的操作需編寫在循環括號外。

初始化;
while (條件表達式) {// 循環體迭代表達式;
}

而for循環語法結構更加緊湊，集成了初始化、條件判斷和迭代更新三個環節于一體。其一般形式如下：

for (初始化; 條件表達式; 迭代表達式) {// 循環體（要重復執行的代碼）
}

3.使用場景

1. for循環:

• 當循環次數固定或可預知時，如遍歷數組或容器的所有元素。
• 需要同時初始化、檢查條件和更新循環變量時，代碼更加整潔。

2. while循環:

• 當循環的持續依賴于一個可能在循環過程中變化的條件時。
• 對于循環次數不確定，或需要在滿足特定條件時開始循環的情況更為合適。
• 當初始化或迭代更新操作較為復雜，不適合放在簡短的循環頭部時。

4.條件控制

1. for循環:

由于其結構特點，循環控制（包括初始化、條件檢查和迭代更新）更規范，易于理解和維護，但靈活性相對較低。

2. while循環:

提供了更高的靈活性，因為條件判斷之外的其他操作都可以自由安排，適合復雜的循環控制邏輯，但可能因為控制流程分散而不易閱讀和調試。

5.小結

選擇for循環還是while循環，應基于具體問題的性質和編程習慣。for循環在處理已知迭代次數或有明確迭代模式的情況時更佳，而while循環則在循環條件更靈活、復雜時展現其優勢。理解兩者的異同，能幫助你更有效地選擇合適的循環結構來解決問題。

二、例題講解

問題：1264 - 4位反序數

類型：for循環

---

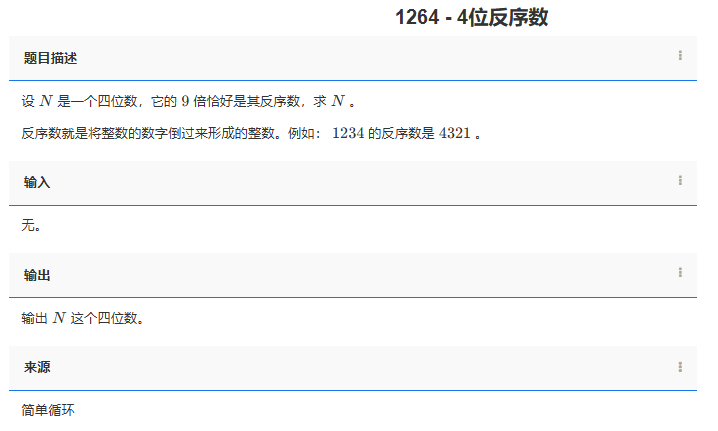
題目描述：

設 N 是一個四位數，它的 9 倍恰好是其反序數，求 N 。
反序數就是將整數的數字倒過來形成的整數。例如： 1234 的反序數是4321 。

輸入：

無。

輸出：

輸出 N 這個四位數。

---

1.分析問題

1. 已知：所有的四位數N；
2. 未知：找出符合條件的數；
3. 關系：滿足N * 9 = temp，其中temp是N的反序數。

2.定義變量

• 初始化變量i為1000，這是因為N是一個四位數，所以搜索范圍從1000開始。
• 聲明變量temp用于存儲N的反序數。

	//二、數據定義 int i=1000,temp;

3.輸入數據

無。

4.數據計算

使用一個for循環遍歷1000到9999之間的所有整數（包括兩端）。

1. 在循環內部，首先通過一系列的除法和取余運算計算出i的反序數并存入temp。具體操作為：

• i%10得到個位數，
• i/10%10得到十位數，
• i/100%10得到百位數，
• i/1000得到千位數，注意這里沒有取余是因為前面的乘法操作已經確保了結果在正確的位置上。
• 然后按照反序重新組合這些數字形成temp。

2. 接著檢查i*9是否等于temp。如果相等，說明找到了符合條件的N。

//四、數據計算 for(;i<10000;i++){temp=i%10*1000+i/10%10*100+i/100%10*10+i/1000;if(i*9==temp){//五、輸出結果 cout<<i<<endl;}}

完整代碼如下：

#include <iostream>
using namespace std;int main() {// 一、分析問題// 目標：尋找一個四位數N，使得N乘以9等于其反序數（即N的數字逆序排列形成的數）。// 二、數據定義int i = 1000, temp; // 初始化計數器i為1000（四位數起始），temp用于存儲當前i的反序數// 三、遍歷并計算// 從1000到9999遍歷所有四位數for (; i < 10000; i++) {// 計算當前數i的反序數temp// 方法是將i的各位數字分離并以相反順序重新組合temp = (i % 10) * 1000 + (i / 10 % 10) * 100 + (i / 100 % 10) * 10 + (i / 1000);// 四、條件判斷// 檢查當前數i乘以9是否等于其反序數tempif (i * 9 == temp) {// 五、輸出結果// 打印滿足條件的數icout << i << endl;}}// 六、程序結束return 0; // 程序執行完畢，返回0表示成功結束
}

---

問題：1085 - 尋找雷劈數

類型：for循環

---

題目描述：

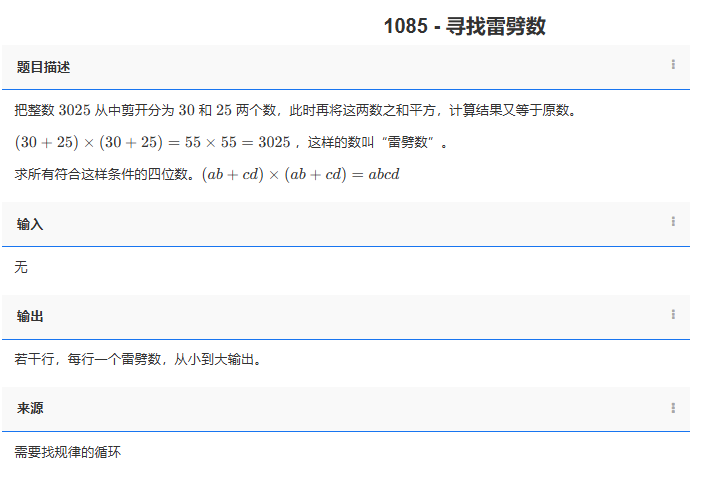
把整數 3025 從中剪開分為 30 和 25 兩個數，此時再將這兩數之和平方，計算結果又等于原數。
(30+25)×(30+25)=55×55=3025 ，這樣的數叫“雷劈數”。
求所有符合這樣條件的四位數。(ab+cd)×(ab+cd)=abcd

輸入：

無

輸出：

若干行，每行一個雷劈數，從小到大輸出。

---

1.分析問題

1. 已知：所有的四位數N；
2. 未知：找出符合條件的數；
3. 關系：滿足條件(AB + CD) * (AB + CD) = ABCD。

2.定義變量

• 定義兩個整型變量ab和cd，分別用來存儲四位數分解后的前兩位和后兩位。

	//二、數據定義 int ab,cd;

3.輸入數據

無。

4.數據計算
使用for循環遍歷所有四位數（1000到9999）。

• 對于每一個遍歷到的數i，通過整除和取余操作將其分為兩部分：ab = i / 100（前兩位），cd = i % 100（后兩位，注意這里得到的是一個0-99的數，但作為計算目的，這不影響結果）。
• 判斷條件(ab + cd) * (ab + cd) == i是否成立，即當前數i是否等于其前兩位與后兩位數字之和的平方。
• 如果條件滿足，說明找到了一個雷劈數。

//四、數據計算 for(int i=1000;i<10000;i++){ab=i/100;cd=i%100;if(i==(ab+cd)*(ab+cd)){//五、輸出結果cout<<i<<endl;}}

完整代碼如下：

#include <iostream>
using namespace std;int main() {// 一、分析問題// 目標：尋找所有的“雷劈數”，即滿足條件的四位數ABCD，其中AB和CD均為兩位數，// 且該四位數等于(AB + CD)乘以(AB + CD)的結果。// 二、數據定義int ab, cd; // 分別用于存儲四位數的前兩位和后兩位組成的兩位數// 三、遍歷四位數范圍進行計算for (int i = 1000; i < 10000; i++) { // 從最小的四位數1000開始，到最大的四位數9999// 提取當前四位數的前兩位(ab)和后兩位(cd)ab = i / 100; // 整除100得到前兩位組成的數字cd = i % 100; // 取模100得到后兩位組成的數字，注意結果包含后兩位，即使第一位為0// 四、條件判斷// 檢查當前數i是否等于其前兩位與后兩位數字之和的平方if (i == (ab + cd) * (ab + cd)) {// 五、輸出結果// 當找到滿足條件的雷劈數時，輸出該數cout << i << endl;}}// 六、程序結束return 0; // 程序執行完畢，返回0表示成功
}

---

問題：1057 - 能被5整除且至少有一位數字是5的所有整數的個數

類型：for循環

---

題目描述：

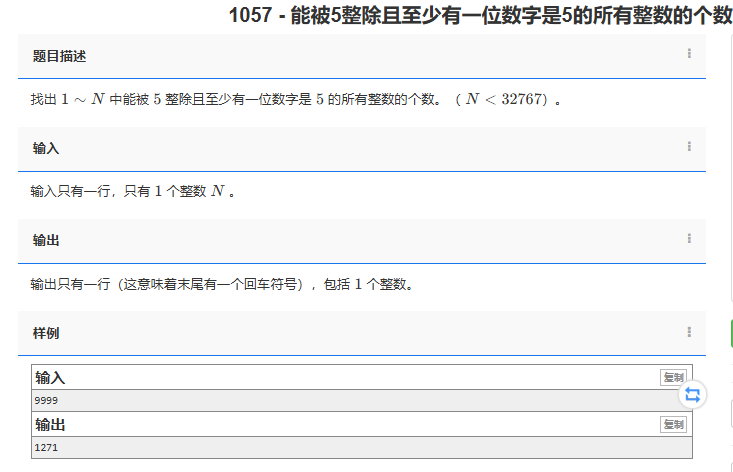
找出1～N 中能被 5 整除且至少有一位數字是 5 的所有整數的個數。（N<32767）。

輸入：

輸入只有一行，只有 1 個整數 N 。

輸出：

輸出只有一行（這意味著末尾有一個回車符號），包括 1 個整數。

樣例：

輸入：

9999

輸出：

1271

---

1.分析問題

1. 已知：1-N的整數 ；
2. 未知：能被5整除且至少有一位數字是5的所有整數的個數sum ；
3. 關系：%5==0 個位=5，十位=5，百位=5，千位=5 。

2.定義變量

• 定義整型變量n用于存儲用戶輸入的上限值。
• 定義整型變量sum初始化為0，用于累計滿足條件的整數個數。

	//二、數據定義 int n,sum=0;

3.輸入數據

• 使用cin >> n;從標準輸入讀取一個整數N，作為搜索范圍的上限。

	//三、數據輸入cin>>n;

4.數據計算

• 使用for循環，初始值設為5（第一個同時滿足能被5整除和包含數字5的整數），每次循環增加5（保證整除5的特性），直到達到或超過N。
• 在循環體內，使用一系列條件語句檢查當前數i的每一位（個位、十位、百位、千位）是否含有數字5。如果任何一個位上的數字為5，則累加器sum加1。
• 注意：這里通過i%10、i/10%10、i/100%10、i/1000%10分別獲取個位、十位、百位、千位上的數字。

//四、數據計算 for(int i=5;i<=n;i+=5){if(i%10==5||i/10%10==5||i/100%10==5||i/1000%10==5){sum++;}}

5.輸出結果

• 輸出滿足條件的整數總數。

//五、輸出結果 cout<<sum;	

完整代碼如下：

#include <iostream>
using namespace std;int main() {// 一、分析問題// 目標：計算1到N之間（包括N），既能被5整除又至少包含一個數字5的所有整數的個數。// 二、數據定義int n, sum = 0; // n為用戶輸入的上限值，sum用于記錄滿足條件的數的個數，初始化為0// 三、數據輸入cin >> n; // 從用戶那里接收一個整數N，作為搜索的上限// 四、數據計算for (int i = 5; i <= n; i += 5) { // 從5開始遍歷，每次增加5，確保數能被5整除// 檢查當前數i的各位（個位、十位、百位、千位）是否有5if (      i % 10 == 5    // 檢查個位是否為5|| (i / 10) % 10 == 5 // 檢查十位是否為5，先除以10再取余|| (i / 100) % 10 == 5 // 檢查百位是否為5|| (i / 1000) % 10 == 5) { // 檢查千位是否為5sum++; // 如果當前數的任何一位是5，sum加1}}// 五、輸出結果cout << sum; // 輸出滿足條件的整數個數return 0; // 程序執行完畢，返回0表示成功
}

---

問題：1392 - 回文偶數？

類型：for循環

---

題目描述：

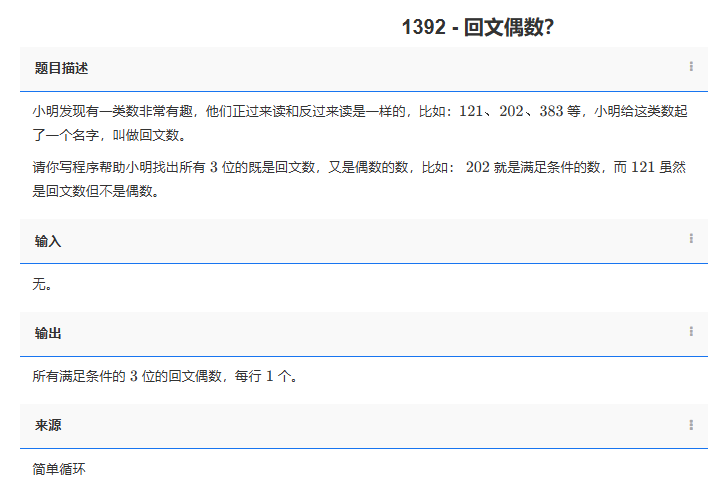
小明發現有一類數非常有趣，他們正過來讀和反過來讀是一樣的，比如：121、202、383 等，小明給這類數起了一個名字，叫做回文數。
請你寫程序幫助小明找出所有 3 位的既是回文數，又是偶數的數，比如： 202 就是滿足條件的數，而 121 雖然是回文數但不是偶數。

輸入：

無。

輸出：

所有滿足條件的 3 位的回文偶數，每行 1 個。

---

1.分析問題

1. 已知：所有的3位數；
2. 未知：所有3 位的既是回文數，又是偶數的數；
3. 關系：%2==0是偶數 、i % 10 == i / 100是回文數。

2.定義變量

無。

3.輸入數據

無。

4.數據計算

• 使用for循環，初始值設為100（第一個三位偶數），每次循環遞增2，直接跳過奇數，提高效率。
• 在循環內部，使用條件if(i%10==i/100)來判斷當前數i是否為回文數。這里檢查了百位和個位是否相等，適用于三位數的回文判斷。
• 當i滿足既是偶數（由于循環增量為2，保證了這一點）又是回文數的條件時，執行輸出操作。

	//四、數據計算 for(int i=100;i<=998;i+=2){if(i%10==i/100){//五、輸出結果 cout<<i<<endl;}}

5.輸出結果

• 使用cout<<i<<endl;輸出滿足條件的數，即既是回文數又是偶數的三位數。

完整代碼如下：

#include <iostream> // 包含標準輸入輸出流庫
using namespace std; // 使用std命名空間，簡化cout和endl的使用int main() { // 程序入口點// 一、分析問題// 目標：找出所有的三位數中，既是回文數也是偶數的數。// 回文數特點：正著讀和倒著讀都一樣的數，對于三位數而言，意味著百位和個位數字相同。// 偶數特點：能被2整除，即數字末尾是0、2、4、6、8。// 二、數據定義與初始化// 通過for循環變量i來遍歷所有可能的三位數，起始值100（第一個三位數），終止值998（最后一個符合條件的偶數三位數）// 三、數據處理（遍歷與判斷）for (int i = 100; i <= 998; i += 2) { // 遍歷所有三位偶數// 判斷條件：i的個位數（i%10）等于百位數（i/100，注意這里進行了整除，得到的是去掉個位和十位后的數）if (i % 10 == i / 100) { // 四、結果輸出// 當找到一個滿足條件的數時，將其輸出cout << i << endl; // 輸出該數并換行}}return 0; // 五、程序結束// 表示程序成功執行完畢，返回操作系統一個狀態碼0，通常代表沒有錯誤。
}

問題：1090 - 同因查找

類型：for循環、簡單循環

---

題目描述：

求出 10 至 1000 之內能同時被2、3、7 整除的數，并輸出。
每行一個。

輸入：

無。

輸出：

按要求輸出滿足條件的數，每行 1 個。

---

1.分析問題

1. 已知：10至1000的數 ；
2. 未知：同時被2、3、7整除的數；
3. 關系：2、3、7都是素數，即除了1和本身不能被其他數整除 。所以想同時被2、3、7整除，那么必然能整除2 * 3 * 7 。

2.定義變量

無。

3.輸入數據

無。

4.數據計算

• 通過for循環，變量i從10開始遞增到999（不包含1000），遍歷這個區間內的所有整數。
• if條件語句檢查當前數i是否能被237（即42，2、3、7的最小公倍數）整除。能被42整除意味著該數可以同時被2、3、7整除。
• 當i滿足條件時，使用cout << i << endl;輸出這個數并換行，以列表形式展示所有滿足條件的整數。

	//四、數據計算 for(int i=10;i<1000;i++){if(i%(2*3*7)==0){//最小公倍數 //五、輸出結果 cout<<i<<endl;}}

完整代碼如下：

#include <iostream> // 引入標準輸入輸出流庫，使得我們可以使用cout進行輸出等操作。
using namespace std; // 使用std命名空間，這樣可以直接調用cout、cin等而無需前綴std::。int main() { // 定義主函數，程序的執行從這里開始。// 一、問題分析說明// 目標：找出10至1000間能同時被2、3、7整除的數。// 邏輯：由于2、3、7均為素數，它們的最小公倍數即它們的乘積（2*3*7=42），任何能被這三數整除的數也能被42整除。// 三、數據處理部分 - 開始循環遍歷指定范圍內的數for(int i = 10; i < 1000; i++) { // 初始化i為10，當i小于1000時循環繼續，每次循環i增加1。// 判斷當前數i是否能被2、3、7的最小公倍數42整除if(i % (2*3*7) == 0) { // 使用取模運算符（%）檢查i除以42的余數是否為0，如果是，則i能被42整除，也就是能同時被2、3、7整除。// 五、結果輸出 - 打印滿足條件的數cout << i << endl; // 輸出滿足條件的數i，并在每個數后換行以便于查看。}}return 0; // 主函數執行完畢，返回0表示程序正常結束。
} // 主函數結束

問題：1446. 人口增長問題

類型：循環應用

---

題目描述：

我國現有 x 億人口，按照每年 0.1% 的增長速度，n 年后將有多少人？

輸入：

一行，包含兩個整數 x 和 n ，分別是人口基數和年數，以單個空格分隔。

輸出：

輸出最后的人口數，以億為單位，保留到小數點后四位。(1≤x≤100,1≤n≤100) 。

樣例：

輸入：

13 10

輸出：

13.1306

---

1.分析問題

1. 已知：初始人口為 x 億人，年增長率為0.1%。
2. 未知：n 年后的人口總數。
3. 關系：每年的人口增長量為當前人口的0.1%，因此，n 年后的總人口可以通過逐年累加當前年人口的0.1%來計算。

2.定義變量

• 定義整型變量 n 存儲年數。
• 定義雙精度浮點型變量 x 存儲以億為單位的初始人口數。

	//二、數據定義 int n;double x; 

3.輸入數據

• 使用 cin 從標準輸入讀取 x（初始人口）和 n（年數）的值。

	//三、數據輸入 cin>>x>>n;

4.數據計算
使用 for 循環模擬 n 年的增長過程。每年：

• 當前人口數 x 增加其0.1%（即 x * 0.001）。

	//四、數據計算 for(int i=1;i<=n;i++){x+=x*0.001;}

5.輸出結果

• 使用 cout 輸出最終人口數，fixed 和 setprecision(4) 用于設定輸出格式，確保人口數保留四位小數。

	//五、輸出結果 cout<<fixed<<setprecision(4)<<x;

完整代碼如下：

#include<bits/stdc++.h> // 包含標準庫中的所有常用頭文件，方便編程但可能增加編譯時間
using namespace std; // 使用std命名空間，省略std::前綴int main(){ // 程序的主入口函數// 一、分析問題// 給定初始人口（x 億），年增長率（0.1%），求n年后的總人口// 二、數據定義int n; // 定義一個整數n，存儲年數double x; // 定義一個雙精度浮點數x，存儲初始人口數（單位：億）// 三、數據輸入cin >> x >> n; // 從用戶輸入中讀取初始人口x（億）和年數n// 四、數據計算for(int i = 1; i <= n; i++){ // 循環n次，模擬每一年的增長x += x * 0.001; // 每年的人口增長為原有人口的0.1%，累加到x上}// 五、輸出結果cout << fixed << setprecision(4) << x; // 設置輸出格式為固定小數點，保留四位小數，然后輸出最終人口數xreturn 0; // 主函數正常結束，返回0表示成功執行
}

三、總結

循環，編程藝術之輪轉，for與while，循環結構是編程中的兩大神器。理解它們的語法構造與適用場景，是在解決編程挑戰中的關鍵。通過實例剖析，我們見證了for循環在具體問題解決中的運用，如求解“4位反序數”、“雷劈數”、“回文偶數”等，以及尋找特定條件數列數的個數。這些實例不僅鞏固了for循環的掌握，也展現了循環結構的靈活性與威力，讓問題解決變得直觀且高效。在NOI的道路上，掌握循環，猶如掌握了通往解謎題的鑰匙，開啟編程世界的大門扉。

四、感謝

如若本文對您的學習或工作有所啟發和幫助，懇請您給予寶貴的支持——輕輕一點，為文章點贊；若覺得內容值得分享給更多朋友，歡迎轉發擴散；若認為此篇內容具有長期參考價值，敬請收藏以便隨時查閱。

每一次您的點贊、分享與收藏，都是對我持續創作和分享的熱情鼓勵，也是推動我不斷提供更多高質量內容的動力源泉。期待我們在下一篇文章中再次相遇，共同攀登知識的高峰！