C語言，排序

前言

? ? ? ? 排序，可以說是數據結構中必不可缺的一環。我們創造數據存儲它，要想知道數據之間的聯系，比較是必不可少的。不然，費勁心思得來的數據若是不能有更多的意義，那么拿到了又有什么用？

????????排序是計算機內經常進行的一種操作，其目的是將一組“無序”的記錄序列調整為“有序”的記錄序列。分為內部排序和外部排序，若整個排序過程不需要訪問外存便能完成，則稱此類排序問題為內部排序。反之，若參加排序的記錄數量很大，整個序列的排序過程不可能在內存中完成，則稱此類排序問題為外部排序。內部排序的過程是一個逐步擴大記錄的有序序列長度的過程。

一. 排序的種類

????????快速排序、希爾排序、堆排序、直接選擇排序不是穩定的排序算法，而基數排序、冒泡排序、直接插入排序、折半插入排序、歸并排序是穩定的排序算法。

? ? ? ? 穩定排序：假設在待排序的文件中，存在兩個或兩個以上的記錄具有相同的關鍵字，在用某種排序法排序后，若這些相同關鍵字的元素的相對次序仍然不變，則這種排序方法是穩定的。其中冒泡，插入，基數，歸并屬于穩定排序，選擇，快速，希爾，歸屬于不穩定排序。

? ? ? ? 具體為什么這些排序是穩定排序，或者是不穩定排序，會在之后進行圖片演示。

? ? ? ? 根據上述介紹可以知道，總共的排序分為8種，接下來我會挑出重要的和大家講解。

二. 排序的實現

? ? ? ? 一下排序都是按照排升序的方式進行的，請讀者注意。如果想要讓排序的功能更加豐富，推薦讀者像qsort這樣的標準函數一樣，傳入比較的函數指針，由于只是講解比較原理，故簡化了。

1. 插入排序

1.1. 原理

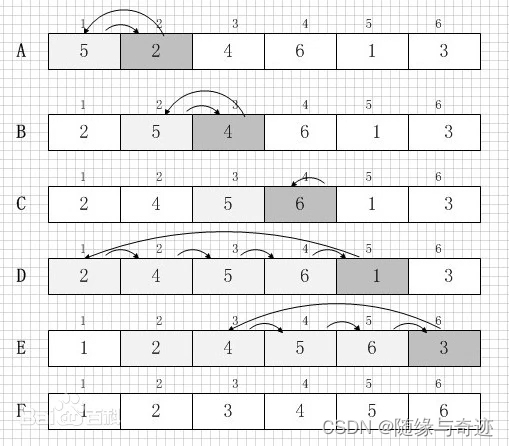
圖1-1 插入排序原理圖

? ? ? ? 如圖1-1所示，開始的時候數據的儲存入第A行所示，我們需要將從第二個數據的位置開始，向前一次插入數據，將小的放在前面。從目標位置向前遍歷的時候，如果目標數據小于比較數據，就將比較的數據向后移動一格。因此我們需要提前記錄目標位置的值。

? ? ? ? 從A行的第二列開始，2小于5，就將5向后移動一位，到頂了，就將2賦給第一列。同理，到了第三列的4,4小于5，就將5向后挪動一列，再繼續比較，4大于2，就不需要挪動2，將4賦給第二列。按照上述規律，依次插入，直到到第E行，將第六列的3插入到第三列為止。

1.2. 代碼

// 插入排序
void InsertSort(int* a, int n)
{// a, 不能為空assert(a);for(int i = 0; i < n - 1; ++i){// 一次插入排序int end = i;int tmp = a[end + 1];while(end >= 0){if(tmp < a[end]) // 升序中， 小于插入的值就挪動數據{a[end + 1] = a[end];end--;}else    // 反之跳出循環賦值{break;}}a[end + 1] = tmp;}
}

2. 希爾排序

2.1. 介紹

????????希爾希爾(Shell's Sort)是插入排序的一種又稱“縮小增量排序”（Diminishing Increment Sort），是直接插入排序算法的一種更高效的改進版本。希爾排序是非穩定排序算法。該方法因 D.L.Shell 于 1959 年提出而得名。

? ? ? ? 希爾排序是一種比較厲害的排序，雖然沒有穩定性，但是排序的時間復雜度是小于O(N^2)的。所以，希爾排序是一種很厲害的排序。快的表現和快速排序、堆排序、歸并排序是一個等級的。

2.2. 原理

圖2-1 希爾排序原理圖

? ? ? ? 如果插入排序是希爾排序的一種特殊情況，插入排序相當于希爾排序增量為1的時候的排序。那么為什么誕生的希爾排序有它的意義呢？從第一趟增量為5的時候，相當于給數據分成了5個部分，大大減小了排序的范圍。在第二趟的排序中，會造成的效果就是，交換的時候每次增量不超過上一次排序的增量也就是5。因此提高了效率。

? ? ? ? 在性能上，希爾排序的時間復雜度區間在O（N^（3/2））到O（N*logN）之間，不需要大量的輔助空間，因此數據排序在中等規模中表現良好。但是對于規模非常大的數據時不是最佳選擇，數據量大的時候仍然推薦快速排序。至于時間復雜度和降低時間復雜度的方法是需要非常復雜的數學模型的，專家們正在研究，如今仍然是數學難題。

2.3. 代碼

// 希爾排序
void ShellSort(int* a, int n)
{// a, 不能為空assert(a);// 希爾排序相當于插入排序中有多次預排序int gap = n;while(gap > 1) //  控制預排序間隔，通常分為三塊{gap = gap / 3 + 1;for(int i = 0; i < n - gap; ++i){// 一次插入排序int end = i;int tmp = a[end + gap];while(end >= 0){if(tmp < a[end]) // 升序中， 小于插入的值就挪動數據{a[end + gap] = a[end];end -= gap;}else    // 反之跳出循環賦值{break;}}a[end + gap] = tmp;}}  
}

3. 選擇排序

3.1. 原理

????????直接選擇排序(Straight Select Sorting) 也是一種簡單的排序方法，它的基本思想是：第一次從R[0]~R[n-1]中選取最小值和最大值，與R[0]、R[n-1]交換，第二次從R[1]~R[n-2]中選取最小值和最大值，與R[1]、R[n-2]交換，....，第i次從R[i-1]~R[n-1-i]中選取最小值和最大值，與R[i-1]、R[n-1-i]交換，.....，重復n/2次，得到一個按排序碼從小到大排列的有序序列。

? ? ? ? 因為非常的簡單，就是反復遍歷數組將最小值最大值分別放到數組首和數組尾，所以時間復雜度很穩定，但也很大，一直都是O（N^2）。

3.2. 代碼

void swap(int* a, int p1, int p2)
{int tmp = a[p1];a[p1] = a[p2];a[p2] = tmp;
}// 選擇排序
void SelectSort(int* a, int n)
{assert(a);int begin = 0, end = n - 1;while(begin < end)  // 一次循環找到最大值和最小值，{int mini = begin, maxi = end;for(int i = begin; i <= end; ++i) // 一次循環找到最大值和最小值{if(a[i] < a[mini]) // 找最小{mini = i;}if(a[i] > a[maxi]) // 找最大{maxi = i;}}if(maxi == begin) // 如果最大值在第一位，就需要改變交換的位置{maxi = mini;}swap(a, begin, mini); // 交換數據swap(a, end, maxi);++begin; // 控制結束循環的條件--end;}
}

4. 堆排序

4.1. 原理

? ? ? ? 原理相關的可以參考之前在二叉樹部分推出的堆排序，是一樣的。利用二叉樹的原理建堆，將最大的數放在堆頂，然后將堆頂的數據放到末尾之后重新從堆頭調整數據，這樣堆的數據每次都會減少一個，直到全部完成排序。

? ? ? ? 建堆的方式選擇向下建堆，完成排序的時間復雜度是O（N*logN）。

4.2. 代碼

// 堆排序
void AdjustDown(int* a, int n, int parent)
{assert(a);// 假設左孩子更大, 公式：child = parent * 2 + 1;int child = parent * 2 + 1;// 孩子節點沒越界就繼續比較while(child < n){// 調整左右孩子，取更小的if(child + 1 < n && a[child + 1] > a[child]){++child;}// 如果滿足條件就交換父子位置并繼續向下遍歷if(a[parent] < a[child]){swap(a, parent, child);parent = child;child = parent * 2 + 1;}else// 反之，跳出循環（無需繼續調整）{break;}}
}void HeapSort(int* a, int n)
{assert(a);//向下調整建堆（大堆）int i = n / 2 - 1;while(i >= 0){AdjustDown(a, n, i);--i;}// 得到降序數組while(--n){swap(a, 0, n);AdjustDown(a, n, 0);}
}

5. 冒泡排序

5.1. 原理

????????冒泡排序（Bubble Sort）是最簡單和最通用的排序方法，其基本思想是：在待排序的一組數中，將相鄰的兩個數進行比較，若前面的數比后面的數大就交換兩數，否則不交換；如此下去，直至最終完成排序。由此可得，在排序過程中，大的數據往下沉，小的數據往上浮，就像氣泡一樣，于是將這種排序算法形象地稱為冒泡排序。

圖5-1 冒泡排序原理圖

? ? ? ? 算法的原理如圖5-1所示，在待排序的一組數中，將相鄰的兩個數進行比較，若前面的數比后面的數大就交換兩數，否則不交換。比如第一趟排序，比較26和28，26小于28故不做改變，到了28和24,28大于24，所以就交換數據位置，再向下比較28和11，仍然需要交換，這樣就完成了一輪，28不在需要比較。然后依次排序。

5.2. 代碼

// 冒泡排序
void BubbleSort(int* a, int n)
{for(int i = 0; i < n - 1; ++i)  // 循環趟數{for(int j = 1; j < n - i; ++j)  // 循環一趟{if(a[j] < a[j - 1]) // 把大的元素往后放，使數據提增{swap(a, j, j - 1);}}}
}

6. 快速排序

6.1. 原理

????????快速排序算法通過多次比較和交換來實現排序，其排序流程如下：

????????（1）首先設定一個分界值，通過該分界值將數組分成左右兩部分。

????????（2）將大于或等于分界值的數據集中到數組右邊，小于分界值的數據集中到數組的左邊。此時，左邊部分中各元素都小于分界值，而右邊部分中各元素都大于或等于分界值。

????????（3）然后，左邊和右邊的數據可以獨立排序。對于左側的數組數據，又可以取一個分界值，將該部分數據分成左右兩部分，同樣在左邊放置較小值，右邊放置較大值。右側的數組數據也可以做類似處理。

????????（4）重復上述過程，可以看出，這是一個遞歸定義。通過遞歸將左側部分排好序后，再遞歸排好右側部分的順序。當左、右兩個部分各數據排序完成后，整個數組的排序也就完成了。

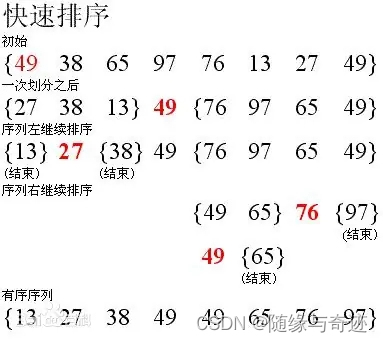
圖6-1 快速排序舉例圖

? ? ? ? 快速排序在分部中分為三種方法：最標準的霍爾法、挖坑法以及前后指針法。如圖6-1所示，快速排序的方法是挖坑法。首先在數組中記錄分界值（這里是49），設置頭指針和尾指針。如果要將數據排列為升序，那么尾指針從后向前遍歷找小于分界值的數（找到了27）停下來，將這個放到之前記錄分界值位置的部分，也可以說是頭指針部分，然后將27填充到49處，表示填坑。這樣27的位置相當于挖了一個坑。然后就然頭指針找大于分界值的數（這里找到的是65），然后將65填充到尾指針的位置處（27）。之后移動尾指針，重復這個循環，直到頭指針和尾指針相遇，將記錄的分界值填入。結果如圖6-1中的一次劃分后所示。每次劃分都能夠確定一個值的具體位置，這里確定的是49。之后將49前后的數據分為新的空間繼續進行劃分即可完成排序。

? ? ? ? 霍爾法，是使用頭指針從左找大，尾指針從后找小，然后交換位置。相遇之后交換分界值的位置，和挖坑法最大的不同之處在于49的位置是最后移動的。

? ? ? ? 前后指針法，前指針找到小于分界值的數就和后指針位置的數交換，然后后指針也向前推進。與前兩者最大的不同是，指針的移動是按照同方向進行的。

6.2. 代碼

int Midi(int* a, int left, int right)
{int midi = (left + right) / 2;if(a[left] > a[midi]){if(a[midi] > a[right]){return midi;}else if(a[left] > a[right]){return right;}else{return left;}}else // a[left] < a[midi]{if(a[midi] < a[right]){return midi;}else if(a[left] < a[right]){return right;}else{return left;}}
}// 快速排序遞歸實現
// 快速排序hoare版本
int PartSort1(int* a, int left, int right)
{int key = left;int begin = left + 1, end = right;while(begin < end){while(begin < end && a[end] >= a[key]){--end;}while(begin < end && a[begin] <= a[key]){++begin;}swap(a, begin, end);}swap(a, key, end);return end;
}// 快速排序挖坑法
int PartSort2(int* a, int left, int right)
{int key = a[left];int begin = left, end = right;while(begin < end){while(begin < end && a[end] >= key){--end;}a[begin] = a[end];while(begin < end && a[begin] <= key){++begin;}a[end] = a[begin];}a[end] = key;return end;
}// 快速排序前后指針法
int PartSort3(int* a, int left, int right)
{int key = a[left];int prev = left, cur = left + 1;while(cur <= right){if(a[cur] < key){++prev;swap(a, prev, cur);}++cur;}swap(a, left, prev);return prev;
}void QuickSort(int* a, int left, int right)
{assert(a);//區間過小直接返回if(left >= right){return;}//如果區間過小使用插入排序// if(right - left  < 10)// {//     SelectSort(a, right - left + 1);// }// 三數取中確定keyint key = Midi(a, left, right);swap(a, left, key);key = PartSort3(a, left, right);QuickSort(a, left, key - 1);QuickSort(a, key + 1, right);
}

6.3. 非遞歸的實現

? ? ? ? 非遞歸的實現就需要解決區間的問題，所以我們需要向之前數據結構中，隊列和棧中借過來存儲區間位置即可。代碼如下：


// 快速排序 非遞歸實現
void QuickSortNonR(int* a, int left, int right)
{assert(a);Stack st;StackInit(&st);StackPush(&st, right);StackPush(&st, left);while(!StackEmpty(&st)){int begin = StackTop(&st);StackPop(&st);int end = StackTop(&st);StackPop(&st);// 三數取中確定keyint keyi = Midi(a, begin, end);swap(a, begin, keyi);keyi = PartSort2(a, begin, end);//區間過小就不入棧if(begin < keyi - 1){StackPush(&st, keyi - 1);StackPush(&st, begin);}if(keyi < end){StackPush(&st, end);StackPush(&st, keyi + 1);}}StackDestroy(&st);
}

7. 歸并排序

7.1. 原理

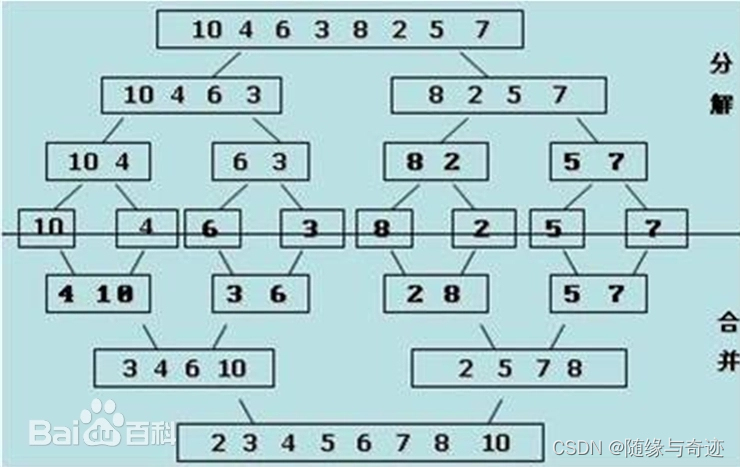
圖7-1 歸并排序原理圖

? ? ? ? 歸并排序，就是將兩組都是有序的數據合成一組的排序。所以對于原來的數組如圖7-1所示，先拆分為不可繼續分割的區間，然后分別將其合并，排列成有序數組，為下一次歸并做準備。例如這里的10和4，組合之后成為[4,10]，3和6組合之后成為[3,6]。然后再將這兩個區間組合成[3,4,6,10]。直到組合完成所有數據。

? ? ? ? ps：實際在代碼中比較需要建立額外的位置存放排序的數據，另外還需要每次排列完成數據后將數據賦值給原來的數組。相互比較的時候也需要注意，會有一個區間的數據沒完全存入，需要分出一步完成該過程。

7.2. 代碼

// 歸并排序，子函數
void _MergeSort(int* a, int* tmp, int left, int right)
{// 區間過小，直接返回if(left >= right){return;}// 分區間int midi = (left + right) / 2;// [left, midi] [mide + 1, right]_MergeSort(a, tmp, left, midi);_MergeSort(a, tmp, midi + 1, right);// 歸并int begin1 = left, end1 = midi;int begin2 = midi + 1, end2 = right;int i = begin1;// 控制比較次數while(begin1 <= end1 && begin2 <= end2){//小的先存if(a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}// 存下剩余部分while(begin1 <= end1){tmp[i++] = a[begin1++];}while(begin2 <= end2){tmp[i++] = a[begin2++];}// 將暫存數據返回memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1));
}// 歸并排序
void MergeSort(int* a, int n)
{// 檢查數組存在assert(a);// 開辟額外的空間暫存排序后數據int* tmp = (int*)malloc(sizeof(int) * n);if(tmp == NULL){perror("malloc fail");return;}// 分裝子函數，實現歸并功能_MergeSort(a, tmp, 0, n - 1);free(tmp);
}

7.3. 非遞歸實現

? ? ? ? 和快速排序一樣，需要解決的是區域劃分的問題。那么如何劃分區間呢？

? ? ? ? 方法是設置區間的大小值，每次排序都按照這個大小劃分區間，沒完成一次歸并就將這個區間的值翻倍，如圖7-1所示，分解區間，開始區間的大小為1，之后是2/4/8。當然劃分區間需要調整，因為數組的大小可能并不是分區間的倍數。如果數組剩下的元素不滿于一個區間，就不需要繼續排序，如果有一個區間但是不足第二個，就需要修剪第二個區間的范圍。

? ? ? ? 代碼如下：

// 歸并排序, 非遞歸
void MergeSortNonR(int* a, int n)
{assert(a);// 開辟額外的空間暫存排序后數據int* tmp = (int*)malloc(sizeof(int) * n);if(tmp == NULL){perror("malloc fail");return;}int gap = 1; // 表示區間間隔while(gap < n){// 將所有區間分為n / gap + 1 份, 每次比較兩個區間for(int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = begin1 + gap - 1;int begin2 = end1 + 1, end2 = begin2 + gap - 1;int j = begin1;if(n - 1 < begin2)// 剩余區間過小，不比較{break;}else if(n - 1 < end2) // 如果區間2在數組結束之前,end2就是數組尾{end2 = n - 1;}//歸并// 控制比較次數while(begin1 <= end1 && begin2 <= end2){//小的先存if(a[begin1] < a[begin2]){tmp[j++] = a[begin1++];}else{tmp[j++] = a[begin2++];}}// 存下剩余部分while(begin1 <= end1){tmp[j++] = a[begin1++];}while(begin2 <= end2){tmp[j++] = a[begin2++];}// 將暫存數據返回memcpy(a + i, tmp + i, sizeof(int) * (2 * gap));}gap *= 2; // 循環的遞增}free(tmp);
}