一、題目描述

給你二叉樹的根結點?root?，請你將它展開為一個單鏈表：

• 展開后的單鏈表應該同樣使用?TreeNode?，其中?right?子指針指向鏈表中下一個結點，而左子指針始終為?null?。
• 展開后的單鏈表應該與二叉樹?先序遍歷?順序相同。

示例 1：

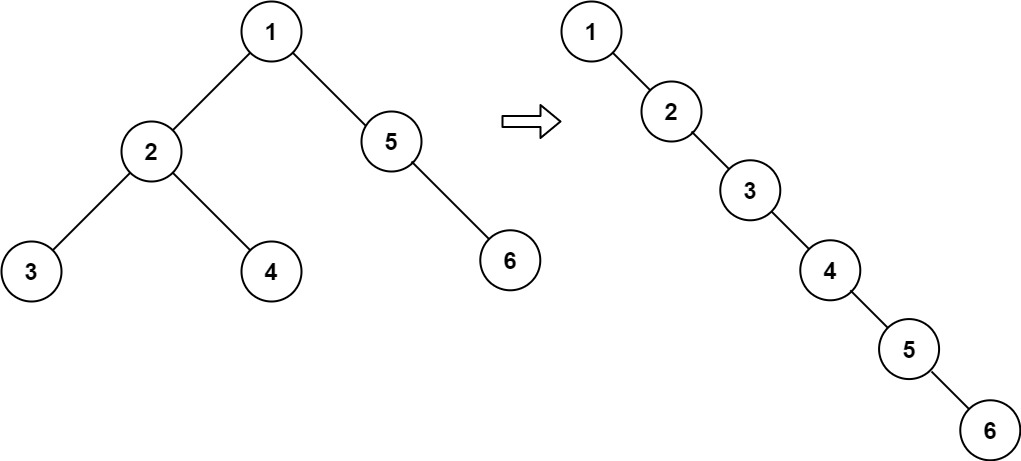
輸入：root = [1,2,5,3,4,null,6]
輸出：[1,null,2,null,3,null,4,null,5,null,6]

示例 2：

輸入：root = []
輸出：[]

示例 3：

輸入：root = [0]
輸出：[0]

提示：

• 樹中結點數在范圍?[0, 2000]?內
• -100 <= Node.val <= 100

二、解題思路

1. 將根節點的左子樹和右子樹拉平。
2. 將拉平后的左子樹作為右子樹，將原來的右子樹接到當前右子樹的末端。

三、具體代碼

class Solution {public void flatten(TreeNode root) {if (root == null) {return;}flatten(root.left);flatten(root.right);TreeNode left = root.left;TreeNode right = root.right;root.left = null;root.right = left;TreeNode p = root;while (p.right != null) {p = p.right;}p.right = right;}
}

四、時間復雜度和空間復雜度

1. 時間復雜度

• 對于每個節點，我們首先遞歸地展平其左子樹，這需要 O(left) 的時間，其中 left 是左子樹中的節點數。
• 然后，我們遞歸地展平其右子樹，這需要 O(right) 的時間，其中 right 是右子樹中的節點數。
• 最后，我們將左子樹移動到右子樹的位置，并找到新的右子樹的末端以連接原始的右子樹。這個操作需要 O(left) 的時間。
• 因此，對于每個節點，我們在最好情況下（沒有子節點）需要 O(1) 時間，在最壞情況下（左右子樹都有）需要 O(left + right) 時間。
• 由于每個節點只被訪問一次，整體時間復雜度是 O(n)，其中 n 是樹中節點的總數。

2. 空間復雜度

• 空間復雜度主要取決于遞歸棧的深度，這通常與樹的高度成正比。
• 在最壞的情況下，樹完全不平衡，例如每個節點都只有左子節點，遞歸棧的深度將是 O(n)，其中 n 是樹中節點的總數。
• 在最好的情況下，樹是完全平衡的，遞歸棧的深度將是 O(log n)。
• 因此，空間復雜度在最壞情況下是 O(n)，在最好情況下是 O(log n)。

五、總結知識點

1. 遞歸：這是一種常用的算法設計技巧，用于將復雜問題分解為更小的子問題。在這個問題中，我們使用遞歸將樹的展平問題分解為子樹的展平問題。

2. 二叉樹遍歷：代碼中隱式地使用了先序遍歷（根-左-右）的順序來展平二叉樹。這是通過遞歸調用?flatten(root.left)?和?flatten(root.right)?實現的。

3. 鏈表操作：展平二叉樹的過程中，我們需要將左子樹轉換為鏈表，并將其連接到根節點的右側，然后將原始的右子樹連接到轉換后的左子樹的末端。這涉及到鏈表的基本操作，如節點的移動和連接。

4. 指針操作：在 Java 中，我們使用?TreeNode?類型的變量來操作樹節點。這些變量實際上是指向樹中節點的指針。代碼中使用了這些指針來修改節點的左右子節點。

5. 邊界條件處理：代碼中首先檢查?root?是否為?null，這是遞歸算法的邊界條件。如果?root?為?null，則直接返回，不再進行遞歸。

6. 引用傳遞：在 Java 中，對象是通過引用傳遞的。這意味著當我們在遞歸調用中傳遞?root.left?和?root.right?時，我們實際上是在傳遞對樹節點對象的引用。因此，在遞歸調用中對這些節點所做的任何修改都會反映到原始樹上。

7. 循環結構：在將左子樹移動到右子樹位置后，我們使用了一個循環結構來找到新的右子樹的末端，以便將原始的右子樹連接起來。

以上就是解決這個問題的詳細步驟，希望能夠為各位提供啟發和幫助。