現有私募基金發行一支特殊基金產品，該基金認購人數上限不超過 30 人， 募集總金額不超過 3000W，每個投資人認購金額不定。該基金只能將募集到的錢用于投資兩支股票，且要求兩支股票投資金額必須相同，且每位投資人的錢只能用于投資一支股票或不投資。問如何在給定募集條件下，實現投資金額最大化。如果無法實現則返回0

解題方法

• 第1步：找到和為偶數的所有子集
• 第2步：將子集傳算法計算：兩子集相等
• 第3步：篩選出和值最大的結果

注意：
[1, 2, 3, 10, 5, 5], 只要求子集和為總和一半，不管哪種劃分方式，都是“最優解”

a: [1, 2 10], [3, 5, 5]

b: [1, 2, 5, 5], [3, 10]

一、代碼與執行結果

具體代碼

1、動態規劃：將列表切分成兩個和值相等的子列表

import random# 動態規劃：將列表切分成兩個和值相等的子列表def can_partition(nums):total_sum = sum(nums)if total_sum % 2 != 0:return Falseif len(nums) == 2: if nums[0] == nums[1]:return ([nums[0]], [nums[1]], nums[0]*2)else:return Falsetarget_sum = total_sum // 2n = len(nums)# ----------------------# 初始化動態規劃表 dp，其中 dp[i][j] 表示前 i 個元素中是否存在和為 j 的子集。dp = [[False] * (target_sum + 1) for _ in range(n + 1)] # 空間: O(n * target_sum)# 初始時，將 dp[0][0] 設為 True。dp[0][0] = True# 創建一個字典 index_map，用于記錄每個元素在原列表中的索引。[1, 5, 11, 5] [1, 5, 5, 11]index_map = {}for i in range(n):if nums[i] not in index_map:index_map[nums[i]] = [i]else:index_map[nums[i]].append(i)# 哈希表# 使用兩層循環遍歷元素和目標和的可能取值，更新動態規劃表 dp。# 對于每個位置 (i, j)，如果前 i-1 個元素中存在和為 j 的子集，# 或者前 i-1 個元素中存在和為 j-nums[i-1] 的子集且第 i 個元素沒有被選擇，# 則 dp[i][j] 為 True。for i in range(1, n + 1): # O(n)for j in range(target_sum + 1): # O(target_sum) -> O(n * target_sum)dp[i][j] = dp[i - 1][j]if j >= nums[i - 1]:dp[i][j] = dp[i][j] or dp[i - 1][j - nums[i - 1]]# 如果動態規劃表中 dp[n][target_sum] 為 True，說明存在一種劃分方式，將列表劃分成兩個和相等的子列表。# 接下來，需要找到具體的劃分方式：if dp[n][target_sum]:# 初始化空列表 subset1 和 subset2_indices，subset1 用于存放第一個子列表的元素，subset2_indices 用于存放第二個子列表的索引。subset1, subset2_indices = [], []i, j = n, target_sum# 從動態規劃表的右下角開始向左上角遍歷，如果第 i 個元素沒有被選擇，則將其加入 subset1 中，同時更新目標和 j。while i > 0 and j > 0:# 如果 dp[i - 1][j] 為 True，說明第 i 個元素沒有被選擇，則將 i 減 1，即考慮前 i - 1 個元素。if dp[i - 1][j]:i -= 1# 如果 dp[i - 1][j] 為 False，說明第 i 個元素被選擇了，則將第 i 個元素加入 subset1 中，并更新目標和 j。else:subset1.append(nums[i - 1])j -= nums[i - 1]subset2_indices.append(i - 1)  # 更新 subset2_indicesi -= 1# 最終得到的 subset2_indices 中存放的是第二個子列表的索引，根據這些索引可以得到第二個子列表 subset2。subset2_indices = set(range(n)) - set(subset2_indices)subset2 = [nums[i] for i in subset2_indices]return subset1, subset2, sum(subset1)*2else:return False# 返回兩個子列表和相加的結果的兩倍，表示劃分成功，否則返回 False。# # Test
# nums = [1, 5, 11, 5]
# print(can_partition(nums))  # Output: ([11], [1, 5, 5])# nums = [1, 5, 5, 11]
# print(can_partition(nums))  # Output: ([11], [1, 5, 5])# nums = [1, 2, 2, 3, 4]
# print(can_partition(nums))  #  Output: ([3, 2, 1], [2, 4])

2、篩選出所有符合要求的子集

# 劃分子集：篩選出所有符合要求（例如和值為偶數、至少包含2個元素等）的子集，并降序排序def subset_sums(lst):total_sum = sum(lst)Len = len(lst)if (Len <= 1) or (Len > 30) or (total_sum > 3000):return Falsedef calc_sum(subset):return sum(subset)def is_even(num):return num % 2 == 0def find_sublists(lst, start, end, path, result): # # 回溯，時間， O(2^n)''' lst：要查找子列表的原始列表start：當前遞歸的起始索引end：遞歸的結束索引（不包括在內）path：當前已構建的子列表result：包含所有符合條件的子列表的列表'''if len(path) >= 2 and is_even(calc_sum(path)) and (len(path) > 2 or path[0] == path[1]):result.append(path.copy())# 遞歸終止條件，當起始索引等于結束索引時，遞歸結束if start == end:return# 遍歷從start到end的索引，每次將當前索引對應的元素添加到path中for i in range(start, end):path.append(lst[i])# 遞歸調用函數，將i+1作為新的起始索引，繼續尋找子列表find_sublists(lst, i + 1, end, path, result)# 在遞歸返回后，彈出最后一個元素，以便嘗試其他可能的子列表path.pop()def sort_and_remove_duplicates(lists): # # O(nlog(n))# 對每個子列表進行排序，并轉換為元組以便于后續去重 sorted_lists = [tuple(sorted(sublist)) for sublist in lists]# 使用集合去除重復的子列表unique_lists = list(set(sorted_lists))# 按照子列表的和值從大到小排序整個列表unique_lists.sort(key=lambda x: sum(x), reverse=True)# 將子列表轉換回列表形式并返回結果return [list(sublist) for sublist in unique_lists]def sort_sublists(lists):sorted_lists = sorted(lists, key=lambda x: calc_sum(x), reverse=True)for i in range(len(sorted_lists)):sorted_lists[i].sort()return sorted_listsresult = []find_sublists(lst, 0, len(lst), [], result)return sort_sublists(sort_and_remove_duplicates(result))

3、測試-生成模擬數據

# 生成模擬數據def split_number(number, parts):# 初始化每個部分為0parts_sum = [0] * partsremaining = number# 循環分配數字直到只剩下最后一個部分for i in range(parts - 1):# 隨機分配數字，確保剩余數字可以被均分parts_sum[i] = random.randint(1, remaining - parts + i + 1)remaining -= parts_sum[i]# 最后一個部分取得所有剩余數字parts_sum[-1] = remainingreturn parts_sumdef generate_random_partitions():# 隨機將 Q 兩次切分成不同的 M 份# M1 和 M2 的個數分別為 1 到 10 之間，這樣設置比其他方法產生的結果更加均衡，防止產生大量1M1 = random.randint(1, 10) M2 = random.randint(1, 10)Q_min = max(M1, M2)# 生成一個 30-1500 內的隨機數Q = random.randint(Q_min, 1500)# 隨機切分 Q 為 M1 份和 M2 份part1 = split_number(Q, M1)part2 = split_number(Q, M2)Randnumber = 30 - M1 + M2total_money = Q * 2balance = 3000 - total_moneybal = random.randint(1, balance)if Randnumber >= 1:R = random.randint(1, Randnumber)if R <= balance:part_balance = split_number(bal, R)else:part_balance = []else:part_balance = []return part1 + part2 + part_balance

4、主程序執行

if __name__ == "__main__":# 示例數據nums = [1, 5, 11, 5]# nums = [1, 5, 5, 11]# nums = [12,7,13,18]# nums = [12,8,13,18]# nums = [1,2,3,4,5,6]# nums = [2,3,4,5,6]# nums = [1,2,3,4,5]# nums = [17,3,8]# nums = [1,1]# nums = [1,2]# nums = [1, 2, 2, 3, 4]# nums = [2, 2, 2, 2, 3]print("示例數據-輸入：", nums)# 模擬數據# nums = generate_random_partitions()# print("模擬數據-輸入：", nums)numss = subset_sums(nums)if numss:# print("子集組合：", numss) # 子集組合，最優解只會在這些子集中產生for nums in numss:result = can_partition(nums)if result:print("輸出：", result) # 和值最大的兩個相等子集breakelse:print("輸出：", 0)

5、輸出

示例數據-輸入： [1, 5, 11, 5]
輸出： ([5, 5, 1], [11], 22)

具體算法過程：

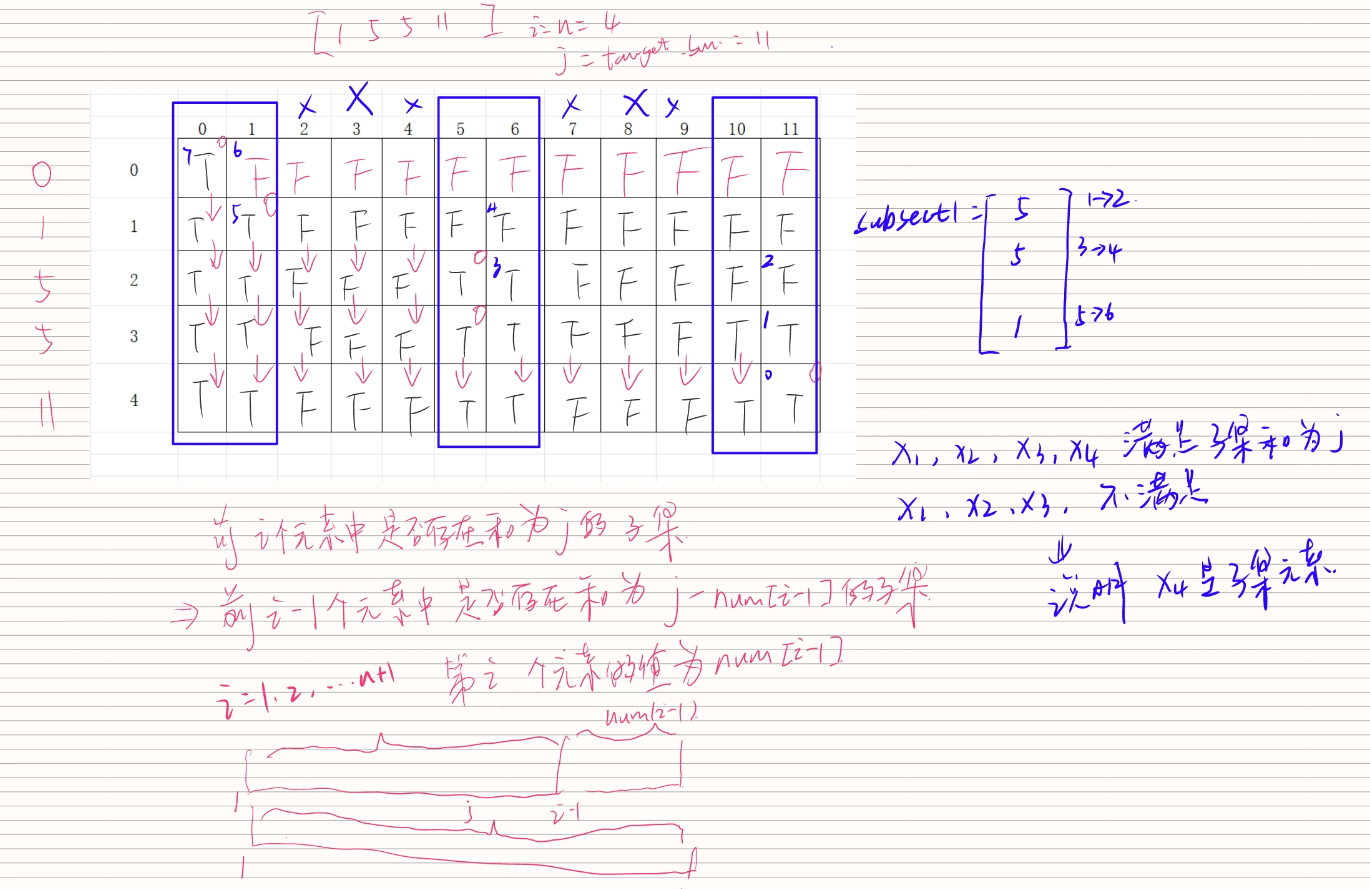
二、函數關鍵信息

• 1、can_partition(nums)函數信息
  函數名稱：can_partition
  關鍵參數和含義：
  nums：輸入的整數列表，表示要判斷是否能將其分割成兩個和相等的子集。
  返回值：
  如果能將 nums 分割成兩個和相等的子集，則返回一個元組 (subset1, subset2, sum(subset1)*2)，其中 subset1 和 subset2 分別為兩個和相等的子集，sum(subset1)*2 為兩個子集的和的兩倍。
  如果不能將 nums 分割成兩個和相等的子集，則返回 False。
  主要變量信息：
  total_sum：nums 列表所有元素的和。
  target_sum：total_sum 的一半，即要達到的子集的目標和。
  n：nums 列表的長度。
  dp：動態規劃數組，dp[i][j] 表示前 i 個元素是否能湊出和為 j 的子集。
  index_map：字典，用于記錄 nums 中每個元素的索引。
  subset1：和相等的子集之一。
  subset2_indices：和相等的另一個子集的索引。
  subset2：和相等的另一個子集。

• 2、subset_sums(lst)函數信息
  函數名稱：subset_sums
  關鍵參數和含義：
  lst：輸入的整數列表，表示要找出其中所有符合條件的子集。
  返回值：
  如果找到符合條件的子集，則返回一個列表，列表中包含所有符合條件的子集，每個子集都是一個列表。
  如果未找到符合條件的子集，則返回 False。
  主要變量信息：
  total_sum：lst 列表所有元素的和。
  Len：lst 列表的長度。
  result：存儲符合條件的子集的列表。
  calc_sum(subset)：計算子集 subset 的和。
  is_even(num)：判斷一個數是否為偶數。
  find_sublists(lst, start, end, path, result)：遞歸查找 lst 中符合條件的子集。
  sort_and_remove_duplicates(lists)：對子集進行排序和去重。
  sort_sublists(lists)：對子集列表進行排序。

三、程序設計原理

• 1、整體思路
  第1步：對于一個列表找到和為偶數的所有子集，限制子集至少包含兩個元素，若只有兩個元素，要求元素值大小相等。對子集和值大小進行降序排序。
  第2步：將符合要求的子集用動態規劃算法進行切分，使得兩子集相等，一旦找到，便終止循環，此時的結果滿足和值最大
  第3步：生成模擬數據，檢驗算法有效性。

• 2、can_partition(nums)函數具體方法
  2.1 函數思路
  首先計算nums數組的總和total_sum，如果total_sum為奇數，則無法分割成等和子集，直接返回False。
  然后計算target_sum為total_sum的一半，問題轉化為在nums數組中找到一組元素的和等于target_sum。
  使用動態規劃算法，定義二維數組dp[i][j]表示在前i個元素中是否存在子集的和為j。初始化dp數組為False，表示初始狀態下不存在子集的和為j。
  遍歷nums數組，對于每個元素nums[i]，遍歷可能的和值j（從target_sum到nums[i]），更新dp[i][j]為True，表示在前i個元素中存在子集的和為j。
  最終如果dp[n][target_sum]為True，表示存在一組子集的和為target_sum，根據dp數組回溯找出這組子集。
  2.2 回溯查找子集：
  當dp[n][target_sum]為True時，從dp數組中回溯查找這組子集。從最后一個元素dp[n][target_sum]開始，如果dp[i-1][j]為True，則說明nums[i-1]不在子集中，將i減一；否則，將nums[i-1]加入subset1中，并將j減去nums[i-1]，繼續向前查找。
  通過回溯找到subset1后，將剩余的元素構成subset2。
  2.3 優化空間：
  使用了index_map來記錄nums數組中每個元素的索引，避免重復計算。
  2.4 返回結果：
  如果存在分割成等和子集的方案，則返回subset1, subset2和sum(subset1)*2；否則返回False。

• 3、subset_sums(lst)函數具體方法
  3.1、 函數思路
  首先計算lst數組的總和total_sum和長度Len，如果Len小于等于1或大于30，或者total_sum大于3000，則直接返回False。
  使用回溯算法，遞歸地尋找符合要求的子集，即和值為偶數、至少包含2個元素。
  對找到的子集進行排序和去重操作。
  3.2、回溯算法：
  定義一個輔助函數find_sublists(lst, start, end, path, result)，其中lst為輸入數組，start和end表示當前搜索范圍的起始和結束位置，path為當前的子集，result為存儲符合要求的子集的列表。
  在回溯過程中，如果當前子集的長度大于等于2且和值為偶數且長度大于2或者前兩個元素相等，則將該子集加入結果中。
  遞歸搜索下一個元素加入子集或者不加入子集的情況，直到搜索完所有元素。
  3.3、排序和去重：
  對于符合要求的子集列表，首先對每個子集進行排序，然后轉換為元組以便于后續去重。
  使用集合去除重復的子集。
  最后按照子集的和值從大到小排序整個列表，并將子集轉換回列表形式返回結果。
  3.4、邊界條件處理：
  在開始時檢查輸入數組的長度和總和是否滿足條件，如果不滿足則直接返回False。

四、復雜度分析

• 1、can_partition(nums)函數復雜度分析
  時間復雜度：程序使用了動態規劃算法來解決分割等和子集問題。外層循環的時間復雜度為O(n)，內層循環的時間復雜度為O(target_sum)，其中n為nums數組的長度，target_sum為nums數組所有元素的和的一半。因此，總體時間復雜度為O(n * target_sum)。
  空間復雜度：程序使用了一個二維數組dp來保存狀態，其大小為(n+1) * (target_sum+1)，因此空間復雜度為O(n * target_sum)。

• 2、subset_sums(lst)函數復雜度分析
  時間復雜度：程序使用了回溯算法來找出所有符合要求的子集，并對結果進行排序和去重。回溯算法的時間復雜度為O(2^{n)，其中n為lst數組的長度。排序和去重操作的時間復雜度為O(nlog(n))，因此總體時間復雜度為O(2}n + nlog(n))。
  空間復雜度：程序使用了遞歸棧來存儲回溯過程中的中間結果，最壞情況下的空間復雜度為O(n)，其中n為lst數組的長度。

• 3、整體復雜度
  can_partition 函數的時間復雜度是O(n * target_sum)，空間復雜度也是O(n * target_sum)。subset_sums 函數的時間復雜度是O(2^n + nlog(n))，空間復雜度是O(n)。
  在整個代碼塊中，首先調用 subset_sums(nums) 函數得到子集組合 numss，這一步的時間復雜度是 subset_sums 的時間復雜度，即O(2^n + nlog(n))。
  然后，對于 numss 中的每個子集，調用 can_partition(nums) 函數，這一步的時間復雜度是O(n * target_sum)。由于 numss 中可能有多個子集，所以整個過程中需要執行多次 can_partition 函數。
  綜上所述，整個代碼塊的總時間復雜度取決于兩個函數中較大的那個復雜度，即O(2^n + n*log(n))，空間復雜度為O(n * target_sum)。