01背包問題 二維

代碼隨想錄

視頻講解：帶你學透0-1背包問題！| 關于背包問題，你不清楚的地方，這里都講了！| 動態規劃經典問題 | 數據結構與算法_嗶哩嗶哩_bilibili

?1.dp數組定義

dp[i][j]? 下標為[0,i]之間的物品，任取放容量為j的背包的最大價值

2.遞推公式

不放物品i： dp[i-1][j]? 去看是否放i-1,還是有j的容量給i-1去放

放物品i ： dp[i-1][j-weight[i]] + value[i]，放了物品i，那么就只有j-weight[i]的容量給i-1個物品去放了，同時要加上我這個物體的價值

?dp[i][j] = max(上面兩個)，取最大價值

3.數組初始化

首先看，i是由i-1推出來的，j是否左上的某一個格子或者正上推出來的（背包剩余容量）

dp[i][0] = 0，背包的容量為0，不管放哪個，價值都為0

dp[0][j] , 當背包可以裝下這個物品開始，dp[0][j]就等于這個物品的價值，裝不下就為0

4.遍歷順序

for(i<weight.size() )? ?物品

? for(j<=bagweight )? ? 背包

對于二維數組實現的01背包，物品和背包的遍歷順序是可以顛倒的，因為左上方和上方是有值的

循環體內是正序還是倒序都是可以的，因為都是根據上一行的數據來進行推導的

因為這里的i層都是由i-1層推到出來的，因此只需要一個一行的一維滾動數組來維護就可以了，不需要整個二維數組

1. dp[j] 容量為j的背包的最大價值為dp[j]

2.遞推公式

不放物品i，就是自己dp[j]，也就是把上一層數據拷貝下來

放物品i ， dp[j-weight[i]] + value[i]

dp[j] = max(上面兩個)

3.初始化

dp[0]=0 ， 背包容量為0的時候，最大價值為0

非零下標都是初始化為0，因為為其他的話，會覆蓋掉遞推公式中算出來的值

4.遍歷順序

for(i<weight.size())? 物品

? for(j=bagweight,j>=weight[0]?)? 背包

采用倒序，是為了防止物品重復選取，比較的數據來自上一輪

正序遍歷就是用同一個物品塞滿背包，每次覆蓋的數據都是同一個物品塞滿的情況

dp【i】【j】的更新只與dp【i-1】【j】和dp【i-1】【j-weight_i】左上角這兩個數據有關，而與右邊的數據無關，那么從右向左遍歷，遍歷時左邊的數據還是上一行的數據沒有更新， 這樣子用一行數組很好的實現了我們的最終目的

在一維中，只能先遍歷物品，再遍歷背包

如果先遍歷背包，再遍歷物品，那記錄的就是只有一個物品

?

代碼隨想錄

視頻講解：動態規劃之背包問題，這個包能裝滿嗎？| LeetCode：416.分割等和子集_嗶哩嗶哩_bilibili

解題思路

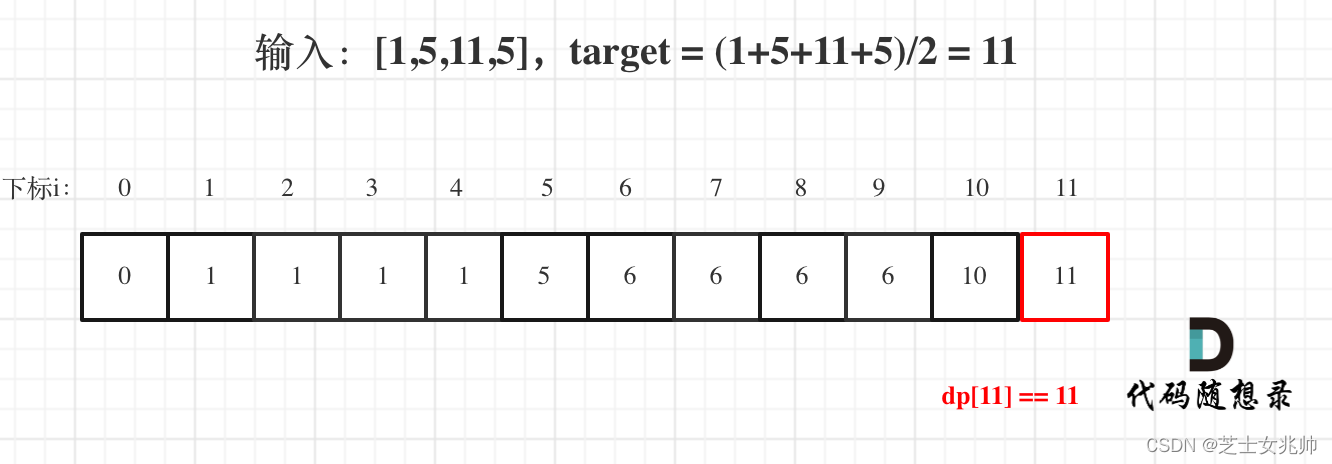
本題元素只能使用1次，并且看能不能裝滿11這個背包

1.dp[j] 容量為j的背包的最大價值，本題最大價值和重量，都是數字本身

2. dp[j] = max(dp[j], dp[j-nums[i] + nums[i]])

3.dp[0] = 0;非零下標，初始為非負整數的最小值，也就是0，因為是由max得來的

4.遍歷順序，先遍歷物品，再遍歷背包，背包是倒序，j要大于等于nums[i]，且每個物品只能使用一次

最后去判斷背包是否裝滿了 dp[target] == target

class Solution {
public:bool canPartition(vector<int>& nums) {int sum =0;for(int i: nums)sum+=i;if(sum%2!=0) return false;int  target = sum/2;vector<int> dp(target+1,0);for(int i=0 ; i< nums.size(); i++)   //物品{for(int j = target; j>=nums[i] ; j--)    //背包{dp[j] = max(dp[j], dp[j- nums[i] ] + nums[i] );   //這題物品和價值是一樣的}}if(dp[target]==target) return true;else return false;}
};

收獲

今天掌握了01背包的理論基礎，本嘗試應用