??

???????????????????????????????????????????博主主頁:LiUEEEEE
??????????????????? ??????????????????????????C語言專欄
????????????????????????????????????????????數據結構專欄
?????????????????????????????????????????力扣牛客經典題目專欄

目錄
- 1、前言
- 2、前序遍歷
- 3、中序遍歷
- 4、后序遍歷
- 5、層序遍歷
- 6、完整代碼展示
- 7、結語
1、前言
??有關二叉樹鏈式結構的四種遍歷方式,是基于二叉樹由鏈式結構組成,故本文不再講解如何實現二叉樹的鏈式結構,以手搓鏈式結構的方式進行四種遍歷方式的講解。
- 結點結構及相關定義展示:
typedef int TreeDataType;typedef struct TreeNode
{TreeDataType val;struct TreeNode* left;struct TreeNode* right;
}TNode;TNode* BuyNode(TreeDataType x);創建二叉樹結點TNode* CreateTree();串連結點組成樹
- BuyNode
TNode* BuyNode(TreeDataType x)
{TNode* tmp = (TNode*)malloc(sizeof(TNode));if (tmp == NULL){perror("BuyNode: malloc fail");return NULL;}tmp->val = x;tmp->left = tmp->right = NULL;return tmp;
}
- CreateTree
TNode* CreateTree()
{TNode* node1 = BuyNode(1);TNode* node2 = BuyNode(2);TNode* node3 = BuyNode(3);TNode* node4 = BuyNode(4);TNode* node5 = BuyNode(5);TNode* node6 = BuyNode(6);node1->left = node2;node1->right = node3;node2->left = node4;node2->right = node5;node3->left = node6;return node1;
}
??再此基礎上我們所構建的書邏輯圖如下所示:

PS.圖中子樹未連接部分均為NULL。
2、前序遍歷
??遍歷的命名規則為,以每一顆樹的根為主要節點(整個樹的根以及子樹的根),以根出現的次序進行命名,下文中的中序后續皆可以此理解。
??前序遍歷:遍歷的順序依次為:根,左子樹,右子樹。
??例如上文中我們手搓的二叉樹,通過前序遍歷的過程并打印的結果如下圖所示:

- 前序遍歷代碼實現
void PreOrder(TNode* root)
{if (root == NULL)return;printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);
}
3、中序遍歷
??中序遍歷:遍歷的順序依次為:左子樹,根,右子樹。
??例如上文中我們手搓的二叉樹,通過中序遍歷的過程并打印的結果如下圖所示:

- 中序遍歷代碼實現
void InOrder(TNode* root)
{if (root == NULL)return;InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}
4、后序遍歷
??后序遍歷:遍歷的順序依次為:左子樹,右子樹,根。
??例如上文中我們手搓的二叉樹,通過后序遍歷的過程并打印的結果如下圖所示:

- 后序遍歷代碼實現
void PostOrder(TNode* root)
{if (root == NULL)return;PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}
5、層序遍歷
??層序遍歷是指按照層數從每層的最左側向右依次打印二叉樹的節點值,如下圖所示:

??但我們實際中很難使用遞歸來操作,使得再打印完2時,通過結點1找到結點3的值打印,故我們需要借助其他工具進行實現,即隊列。
??操作原則是,先將根結點1輸入到隊列中,在打印根結點1時,將結點1的左結點與右結點依次輸入進隊列,并將結點1從隊列中刪除,以此往復,直至在隊列中遇見空結點。
??對此本文不再對隊列相關的知識進行講解,如有需要回看博文:
???????????????????? 隊列的實現(使用鏈表)
??邏輯思路如下圖所示:

- 層序遍歷代碼實現
void LevelOrder(TNode* root)
{Queue pq;QueueInit(&pq);if (root)QueuePush(&pq, root);while (!QueueEmpty(&pq)){TNode* front = QueueFront(&pq);QueuePop(&pq);printf("%d ", front->val);if (front->left)QueuePush(&pq, front->left);if (front->right)QueuePush(&pq, front->right);}QueueDestroy(&pq);
}
- 四種遍歷方式結果展示
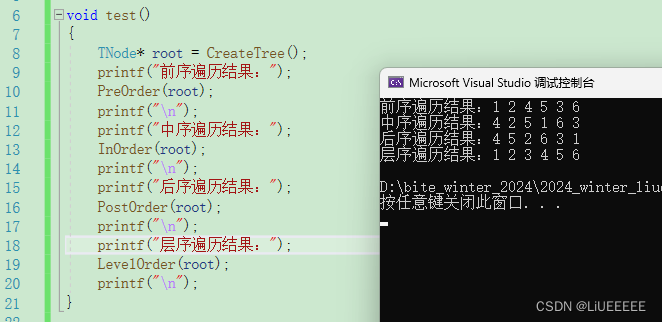
6、完整代碼展示
?? P,S.本章節所展示代碼不包含隊列代碼,如有需求請自行添加。
- Tree.h
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>typedef int TreeDataType;typedef struct TreeNode
{TreeDataType val;struct TreeNode* left;struct TreeNode* right;
}TNode;TNode* BuyNode(TreeDataType x);TNode* CreateTree();void PreOrder(TNode* root);void InOrder(TNode* root);void PostOrder(TNode* root);void LevelOrder(TNode* root);
- Tree.c
#include "Tree.h"
#include "Queue.h"TNode* BuyNode(TreeDataType x)
{TNode* tmp = (TNode*)malloc(sizeof(TNode));if (tmp == NULL){perror("BuyNode: malloc fail");return NULL;}tmp->val = x;tmp->left = tmp->right = NULL;return tmp;
}TNode* CreateTree()
{TNode* node1 = BuyNode(1);TNode* node2 = BuyNode(2);TNode* node3 = BuyNode(3);TNode* node4 = BuyNode(4);TNode* node5 = BuyNode(5);TNode* node6 = BuyNode(6);node1->left = node2;node1->right = node3;node2->left = node4;node2->right = node5;node3->left = node6;return node1;
}void PreOrder(TNode* root)
{if (root == NULL)return;printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);
}void InOrder(TNode* root)
{if (root == NULL)return;InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}void PostOrder(TNode* root)
{if (root == NULL)return;PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}void LevelOrder(TNode* root)
{Queue pq;QueueInit(&pq);if (root)QueuePush(&pq, root);while (!QueueEmpty(&pq)){TNode* front = QueueFront(&pq);QueuePop(&pq);printf("%d ", front->val);if (front->left)QueuePush(&pq, front->left);if (front->right)QueuePush(&pq, front->right);}QueueDestroy(&pq);
}
- TreeTest.c
#include "Tree.h"void test()
{TNode* root = CreateTree();printf("前序遍歷結果:");PreOrder(root);printf("\n");printf("中序遍歷結果:");InOrder(root);printf("\n");printf("后序遍歷結果:");PostOrder(root);printf("\n");printf("層序遍歷結果:");LevelOrder(root);printf("\n");
}int main()
{test();return 0;
}
7、結語

??十分感謝您觀看我的原創文章。
??本文主要用于個人學習和知識分享,學習路漫漫,如有錯誤,感謝指正。
??如需引用,注明地址。



















