【數據結構】紅黑樹——領略天才的想法

個人主頁：東洛的克萊斯韋克-CSDN博客??

祝福語：愿你擁抱自由的風? ? ? ?

二叉搜索樹

AVL樹

紅黑樹概述

性質詳解

效率對比

旋轉操作

元素操作

代碼實現

二叉搜索樹

【數據結構】二叉搜索樹-CSDN博客

AVL樹

【數據結構】AVL樹——平衡二叉搜索樹-CSDN博客

紅黑樹概述

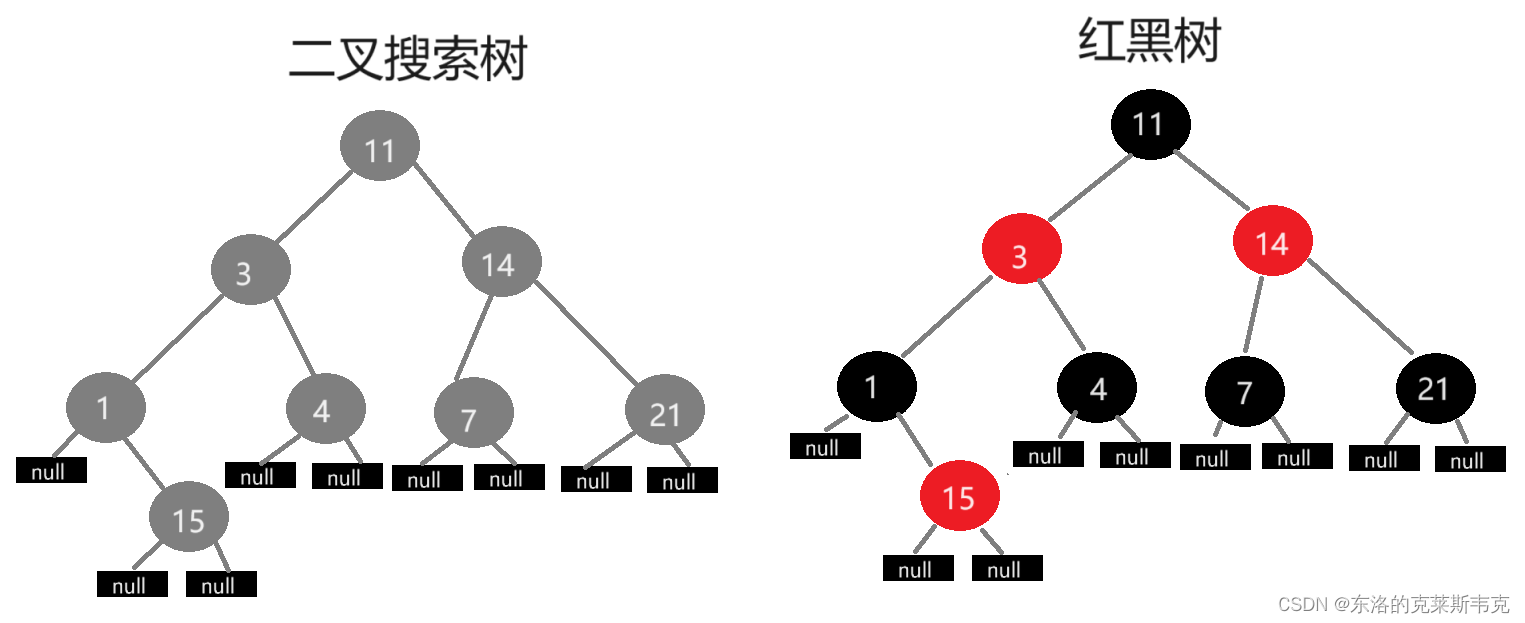
概念

在二叉搜索樹的基礎上符合一下性質便是紅黑樹

每一個節點不是紅色就是黑色

根節點一定是黑色

空節點一定是黑色

父親節點和孩子節點不能是連續的紅色節點

每一條根節點至空節點路徑上的黑色節點的數量一定相等

性質詳解

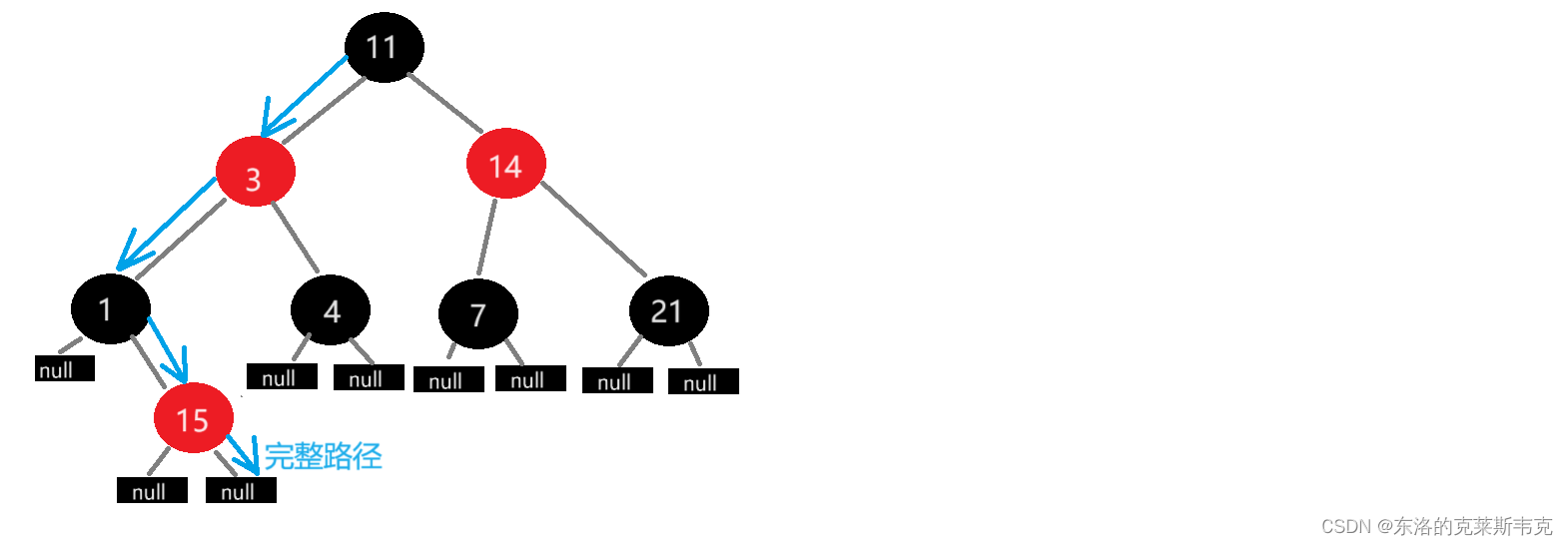
理解路徑

紅黑樹中，一條完整路徑不是從葉子節點溯源至根節點，而是從空節點溯源至根節點

理解最長和最短路徑

如果全是黑色節點，紅黑樹就是一顆滿二叉樹，因為每條路徑的黑色節點數量相等

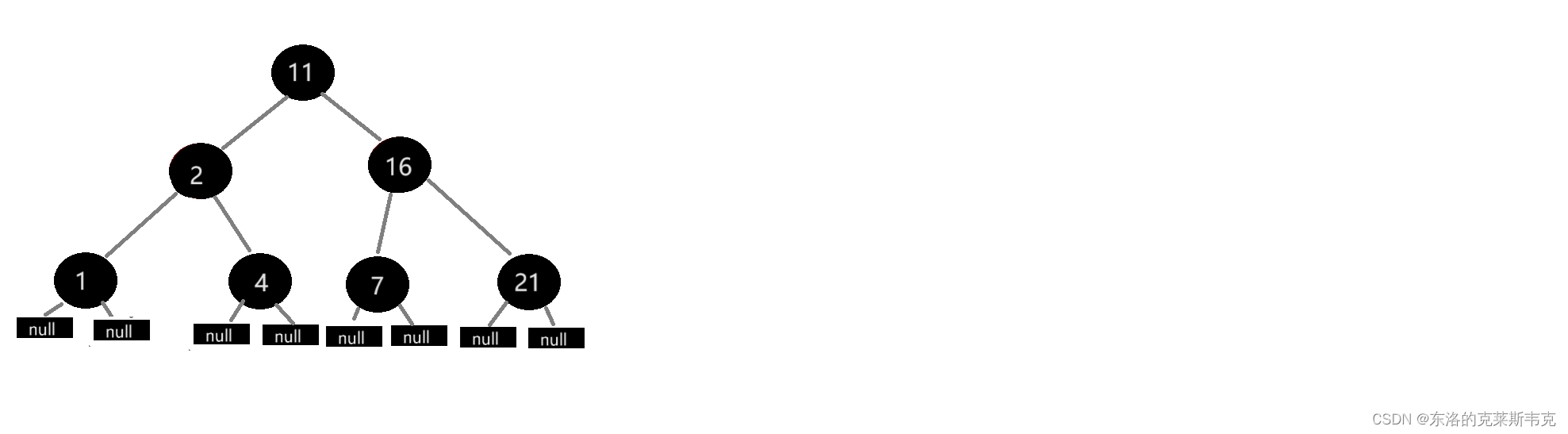那么這顆樹的每條完整路徑都是最短路徑，

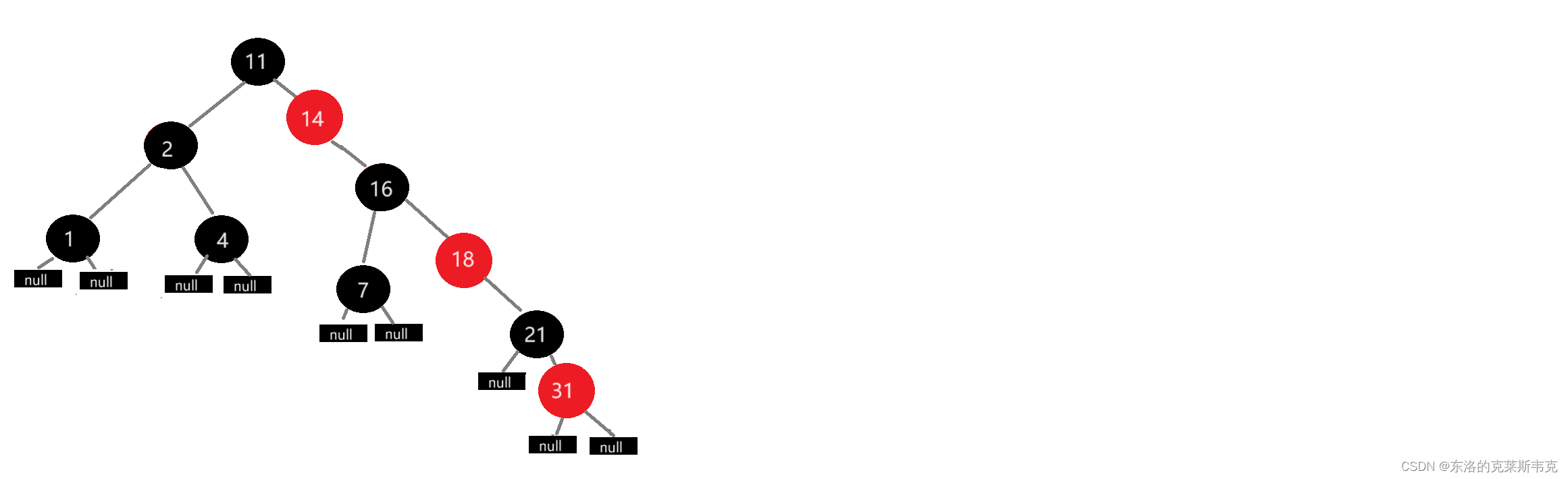
如果在一條路徑上紅黑節點間隔（不允許連續的有紅色節點），那么該路徑為最長路徑。

紅黑樹規則

那么最長路徑是最短路徑的兩倍。這便是紅黑樹的平衡規則。

滿二叉樹的平衡條件是左右子樹高度差為0，AVL樹的平衡條件是左右子樹高度差小于等于 1，相比于前兩棵樹平衡條件，紅黑樹是一種弱平衡。

紅黑樹和AVL樹一樣，只要保證自己的平衡規則不被打破，就能使自己不退化為類似于鏈表的結構。

退化成類似鏈表的結構——插入的數據接近有序或插入大量的數據不夠隨機或進行了一些插入刪除等操作。

效率對比

查找效率

從直覺上講，紅黑樹只是維持一種弱平衡，在最壞情況下，紅黑樹的高度是AVL樹高度的兩倍，那么紅黑樹查找數據的效率也應該比AVL樹低兩倍才對，為什么我們認為紅黑樹是一種更優的數據結構呢？下面小編帶大家算筆賬

2的40次方是一萬億，也就是說用滿二叉樹存一萬億個數據高度為40。AVL樹是有高度差的，所以最壞情況下會查找40多次，而紅黑樹最壞情況下會找80多次。

那么對于cpu而言，找40多次和找80多次有區別嗎？答案是沒有的，現在的cpu每秒鐘可以運算十億次甚至幾百億。

可以理解為，在查找數據的效率上AVL樹和紅黑樹是一樣的。那么，紅黑樹的優勢在哪里呢？

插入刪除效率

不管是紅黑樹還是AVL樹，如果打破平衡都需要旋轉這一操作恢復平衡，旋轉所付出的時間復雜度為 $O(1)$ 。對于AVL樹而言，需要溯源更新平衡因子，對于紅黑樹而言，需要溯源更新節點顏色，溯源更新最壞情況下是從葉子節點更新到根節點，所付出的時間復雜度為 $O(logN)$ 。

因為AVL樹的高度差小于等于1，平衡很容易被打破，要維持平衡就需要不斷地付出 $O(1)$ 和 $O(logN)$ 來維持平衡。

那么紅黑樹維持弱平衡就不需要總是付出這樣地代價，所以紅黑樹是一種更優的數據結構

旋轉操作

旋轉操作不是AVL樹或紅黑樹特有的，旋轉一次的本質是讓二叉搜索樹的某棵子樹的高度減一。

對于紅黑樹而言，最長路徑是最短路徑的二倍加一，就意味著打破平衡，需要通過旋轉讓最長路徑上的某棵子樹高度減一來恢復平衡。旋轉后需要更新節點的顏色，具體要怎么控制顏色下面細講，現在看一下旋轉操作吧

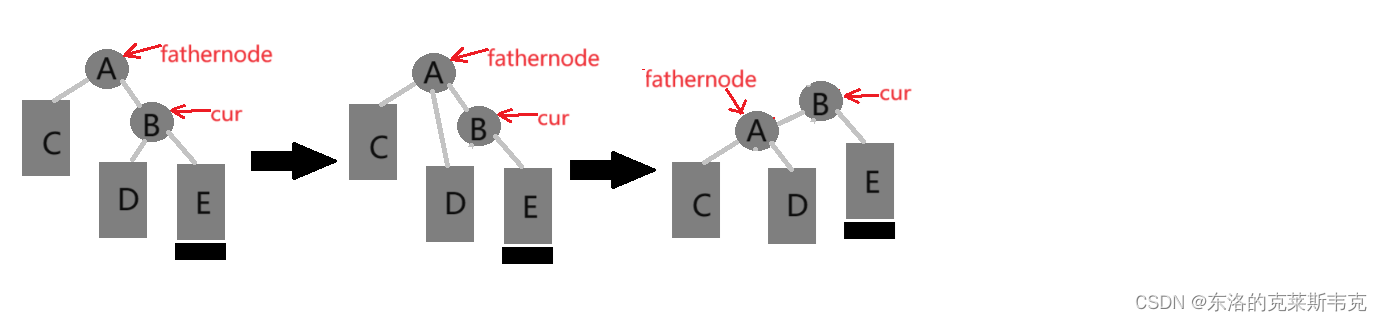
左單旋：新節點插入較高右子樹的右側——對fathernode

void RevolveLeft(node *& fathernode)//左單旋      
{node* cur = fathernode->_right; //父親節點的右孩子fathernode->_right = cur->_left; //更改指向關系if (cur->_left != nullptr) //特殊情況cur->_left->_FatherNode = fathernode;//更改指向關系cur->_FatherNode = fathernode->_FatherNode;//更改指向關系if (fathernode->_FatherNode != nullptr) //為空是特殊情況，{if (fathernode->_FatherNode->_right == fathernode){fathernode->_FatherNode->_right = cur;//更改指向關系}else{fathernode->_FatherNode->_left = cur;//更改指向關系}}cur->_left = fathernode;//更改指向關系fathernode->_FatherNode = cur;//更改指向關系}

右單旋：新節點插入較高左子樹的左側——對fathernode

void RevolveRight(node *& fathernode) //右單旋
{node* cur = fathernode->_left; //父親節點的左節點fathernode->_left = cur->_right;//更新指向關系if (cur->_right != nullptr) //特殊情況cur->_right->_FatherNode = fathernode;//更新指向關系cur->_FatherNode = fathernode->_FatherNode;//更新指向關系if (fathernode->_FatherNode != nullptr)//特殊情況{if (fathernode->_FatherNode->_right == fathernode){fathernode->_FatherNode->_right = cur;//更新指向關系}else{fathernode->_FatherNode->_left = cur;//更新指向關系}}cur->_right = fathernode;//更新指向關系fathernode->_FatherNode = cur;//更新指向關系}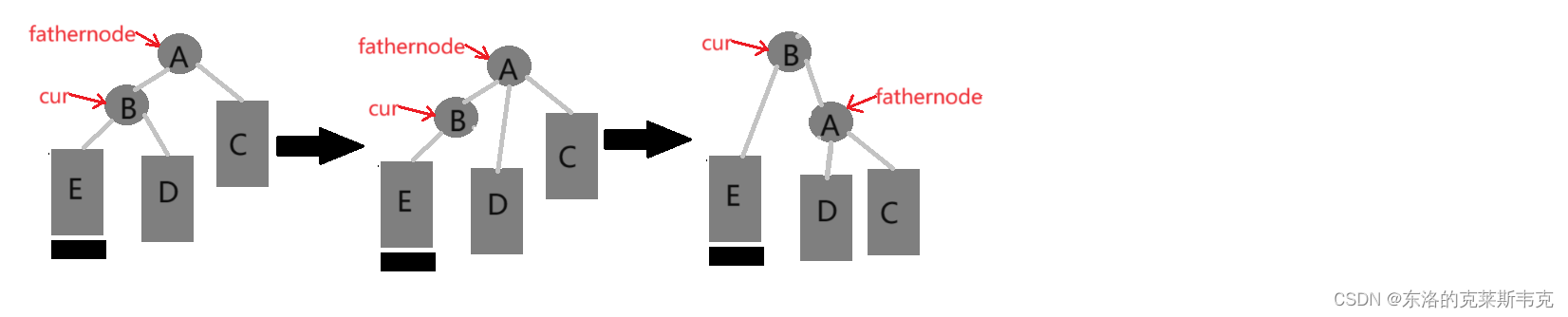

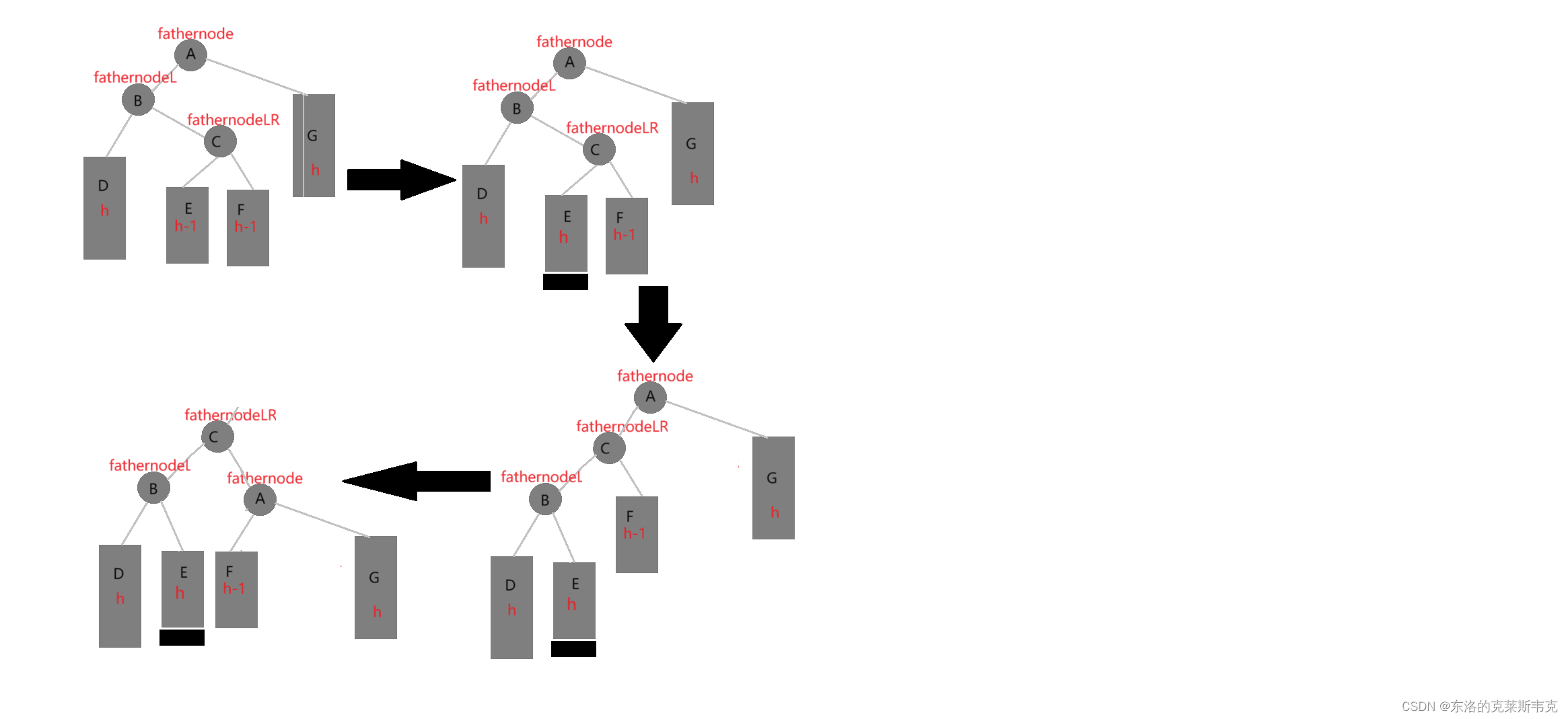
左右雙旋：新節點插入在較高左子樹的右側——先對fathernodeL左單旋再對fathernodeLR右單旋

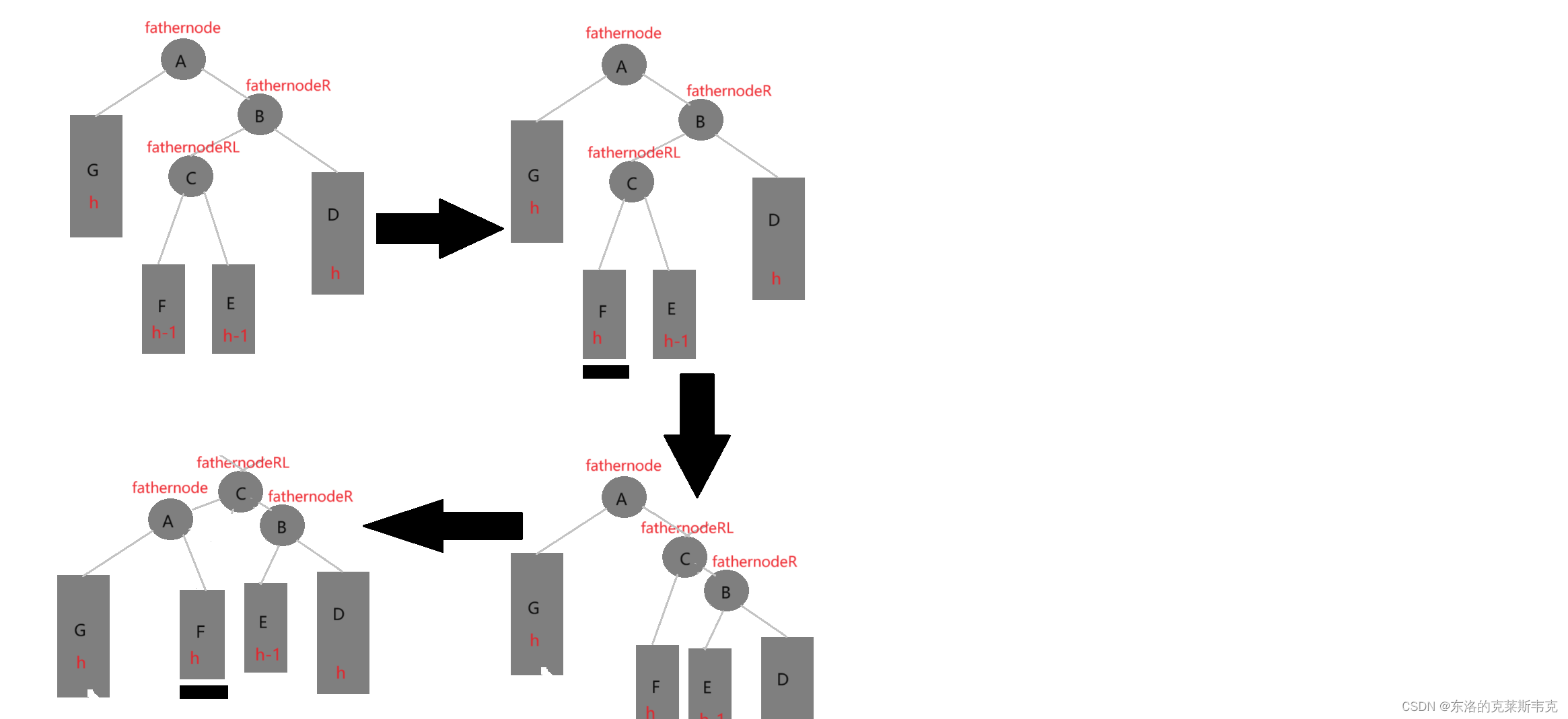
右左雙旋：新節點插入再較高右子樹的左側——先對fathernodeR右單旋再對fathernodeRL左單旋

元素操作

我們再來理解一下紅黑樹兩條核心性質

父親節點和孩子節點不能是連續的紅色節點

每一條根節點至空節點路徑上的黑色節點的數量一定相等

紅黑樹插入的新節點應該是黑色還是紅色呢？

也就是說，插入紅色節點可能會破壞第一條性質，插入黑色節點會破壞第二條性質。第一條性質被破壞只影響了當前路徑，而第二條性質被破壞影響的是所有路徑。所以插入新節點的顏色是紅色。

如果新插入節點的父親節點是黑色，那么不會破壞任何性質，如果新插入節點的父親節點是紅色該怎么辦呢？

顏色管理

下面介紹紅黑樹如何通過管理顏色來判斷是否需要旋轉，為了方便討論討論，給以下節點起個別名，

父親節點：Father

孩子節點：child（父親節點的孩子節點）

祖父節點：grandfather（父親節點的父親節點）

叔叔節點：uncle（如果父親節點是祖父節點的左孩子，叔叔節點就是祖父節點的右孩子，反之亦然）

如果新節點的父親節點為黑，插入成功。如果父親節點為紅，需要溯源更新顏色，規則如下：

如果uncle存在且為紅色，Father和uncle變為黑色，grandfather變為黑色，讓grandfather變為child，繼續溯源更新。

如果更新至整棵樹的根節點（Father為空），讓根節點置黑，或uncle為空或uncle黑色，停止溯源更新（uncle為空或uncle黑色后面會討論）。

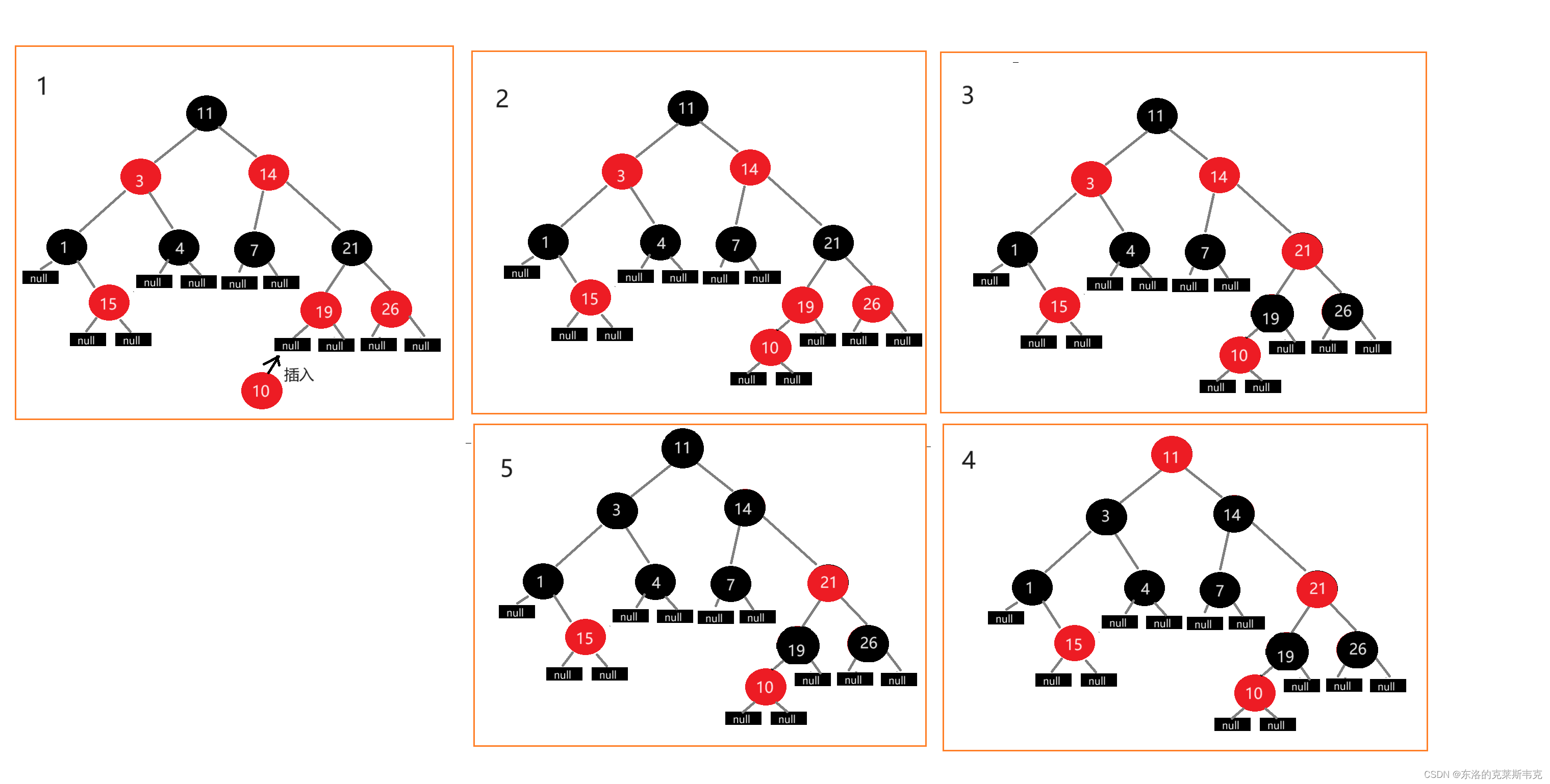
如果uncle不存在，或uncle存在且為黑，說明紅黑樹的平衡被打破了，此時就不需要溯源更新顏色了，需要旋轉來恢復紅黑樹的平衡，旋轉之后再更新Father，grandfather或child的顏色

右單旋顏色更新：

Father成為了根需要變成黑色節點，Father旋轉之前的孩子節點為黑，該孩子會成為grandfather左孩子，grandfather需要變成紅節點。

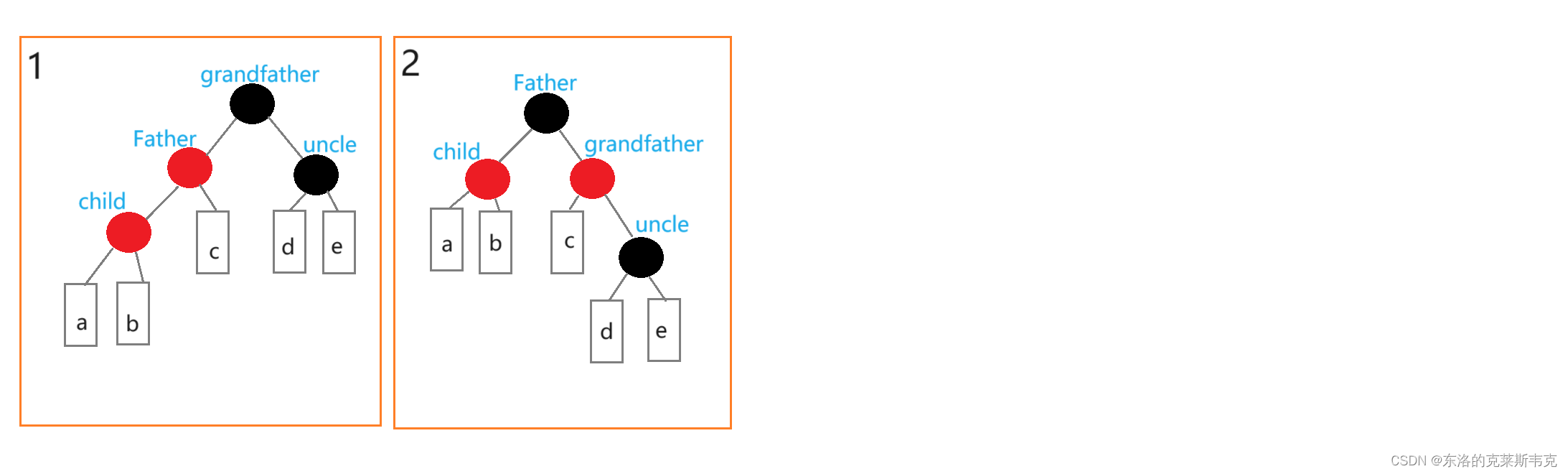
為什么Father旋轉之前的孩子節點為黑呢？因為數據是一個一個插入的，新節點只會和一條路徑上的父親節點沖突，如果這是一顆正常的紅黑樹，Father旋轉之前的孩子節點只能為黑色。Father作為根是黑色的，Father的孩子節點也只能是紅色的。下面的旋轉也一樣

左單旋顏色更新：

還是和右單旋一樣，Father成了根需要變成黑色，grandfather需要變成紅色。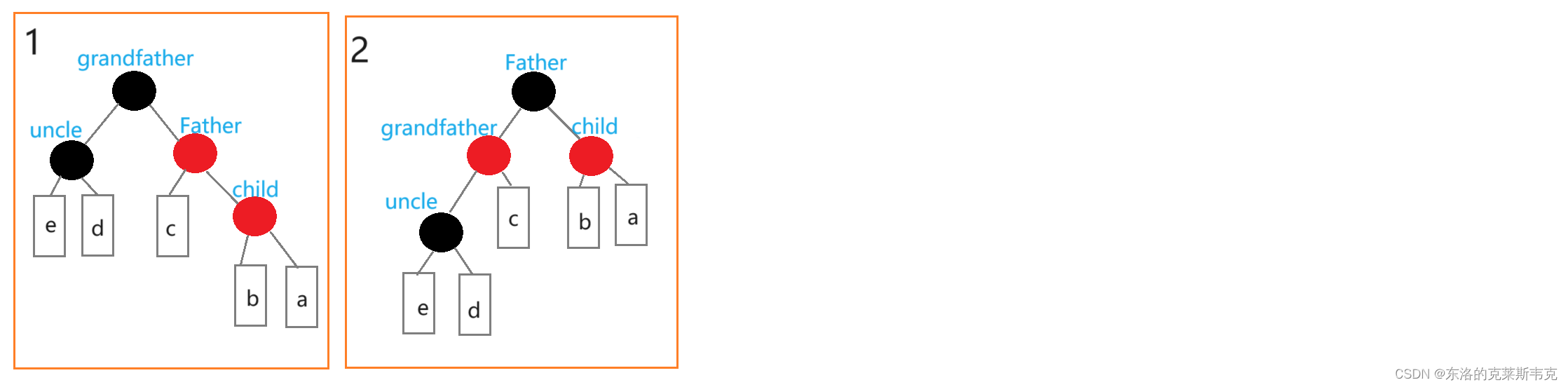

雙旋顏色更新：

無論是左右雙旋還是右左雙旋，最終都是child變成了根，grandfather和Father變成了child的左右孩子，grandfatjie作為孩子需要變成紅色。

代碼實現

【C++】詳解C++的模板-CSDN博客

enum Color { RED, BLACK };    template <class K>
class RBTreeNode
{
public:typedef RBTreeNode <K> node_type;   K _ky;   node_type* _left;node_type* _right;node_type* _FatherNode;  Color _color;RBTreeNode(const K& key):_ky(key),_left(nullptr),_right(nullptr), _FatherNode(nullptr)  ,_color(RED){}};template <class K> 
class RBTree
{
public:typedef RBTreeNode <K> node_type;RBTree():_root(nullptr)    {}bool Insert(const K& key)//插入元素     {////if (nullptr == _root) //是否是空樹{_root = new node_type(key);_root->_color = BLACK;     return true;}//node_type* cur = _root;node_type* fathernode = nullptr;  while (cur){if (cur->_ky < key)    {fathernode = cur;  cur = cur->_right;}else if (cur->_ky > key)     {fathernode = cur;cur = cur->_left;}else{return false;}}cur = new node_type(key); //新插入節點 if (fathernode->_ky < cur->_ky)    {fathernode->_right = cur;cur->_FatherNode = fathernode;}else{fathernode->_left = cur;cur->_FatherNode = fathernode;}while (fathernode && fathernode->_color == RED)  {node_type* grandfather_node = fathernode->_FatherNode;node_type* unclenode = nullptr;if (fathernode == grandfather_node->_left) //父親節點是祖父節點的左孩子{unclenode = grandfather_node->_right; //叔叔節點是祖父節點的右孩子if (unclenode == nullptr || unclenode->_color == BLACK){if (cur == fathernode->_left)  {RevolveRight(fathernode);fathernode->_color = BLACK;grandfather_node->_color = RED; }else if (cur == fathernode->_right){RevolveLeft(fathernode);RevolveRight(cur);cur->_color = BLACK;   grandfather_node->_color = RED;     }}else{fathernode->_color = BLACK; //父親變黑unclenode->_color = BLACK;  //叔叔變黑grandfather_node->_color = RED; //爺爺變紅cur = grandfather_node;fathernode = cur->_FatherNode; }}else//父親節點是祖父節點的右孩子{unclenode = grandfather_node->_left; //叔叔節點是祖父節點的左孩子       if (unclenode == nullptr || unclenode->_color == BLACK){if (cur == fathernode->_right){RevolveLeft(fathernode);   fathernode->_color = BLACK;grandfather_node->_color = RED;}else if (cur == fathernode->_left){RevolveRight(fathernode);RevolveLeft(cur);     cur->_color = BLACK;grandfather_node->_color = RED;}}else  {fathernode->_color = BLACK; //父親變黑unclenode->_color = BLACK;  //叔叔變黑grandfather_node->_color = RED; //爺爺變紅cur = grandfather_node;fathernode = cur->_FatherNode;}}}_root->_color = BLACK;  return true;}private:void RevolveLeft(node_type*& fathernode)//左單旋        {node_type* cur = fathernode->_right;  fathernode->_right = cur->_left;if (cur->_left != nullptr)cur->_left->_FatherNode = fathernode;cur->_FatherNode = fathernode->_FatherNode;if (fathernode->_FatherNode != nullptr){if (fathernode->_FatherNode->_right == fathernode){fathernode->_FatherNode->_right = cur;}else{fathernode->_FatherNode->_left = cur;}}cur->_left = fathernode;fathernode->_FatherNode = cur;}void RevolveRight(node_type*& fathernode) //右單旋 {node_type* cur = fathernode->_left;  fathernode->_left = cur->_right;if (cur->_right != nullptr)cur->_right->_FatherNode = fathernode;cur->_FatherNode = fathernode->_FatherNode;if (fathernode->_FatherNode != nullptr){if (fathernode->_FatherNode->_right == fathernode){fathernode->_FatherNode->_right = cur;}else{fathernode->_FatherNode->_left = cur;}}cur->_right = fathernode;fathernode->_FatherNode = cur;}node_type* _root;
};