存貯模型中的基本概念
模型：
基本要素：
（1）需求率：單位時間內對某種物品的需求量，用D表示。
（2）訂貨批量：一次訂貨中，包含某種貨物的數量，用 Q表示。
（3）訂貨間隔期：兩次訂貨之間的時間間隔，用 T表示。
基本費用：
（1）訂貨費：每組織一次生產、訂貨或采購的費用，通常認為與定購數量無關，
記為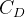 
。
（2）存貯費：所有用于存貯的全部費用，通常與存貯物品的多少和時間長短有關。
單位存貯費記為 
。
（3）短缺損失費：由于物品短缺所產生的一切損失費用，通常與損失物品的多少
和短缺時間的長短有關，記為 
。
存貯策略：
（1） t 循環策略：不論實際的存貯狀態如何，總是每隔一個固定的時間 t ，補充
一個固定的存貯量 Q 。
（2）( t, S) 策略：每隔一個固定的時間 t 補充一次，補充數量以補足一個固定的
最大存貯量 S 為準。因此，每次補充的數量是不固定的，要視實際存貯量而定。當存
貯（余額）為 I 時，補充數量為 Q = S ? I 。
（3）( s, S) 策略：當存貯（余額）為 I ，若 I > s ，則不對存貯進行補充；若 I ≤ s ，
則對存貯進行補充，補充數量 Q = S ? I 。補充后達到最大存貯量 S 。 s 稱為訂貨點（或
保險存貯量、安全存貯量、警戒點等）。在很多情況下，實際存貯量需要通過盤點才能
得知。若每隔一個固定的時間 t 盤點一次，得知當時存貯 I ，然后根據 I 是否超過訂貨
點 s ，決定是否訂貨、訂貨多少，這樣的策略稱為( t, s, S)策略。
基本存貯模型
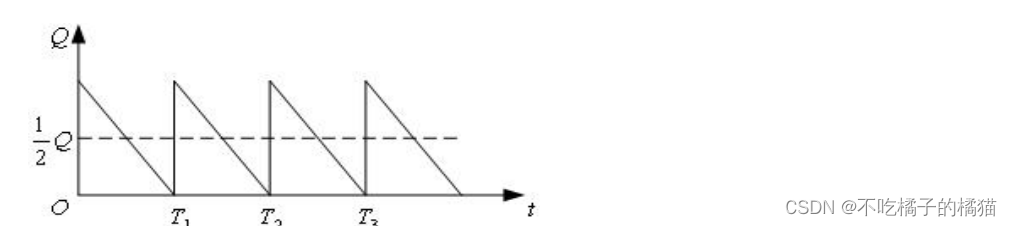
模型一：不允許缺貨，補充時間極短（基本的經濟訂購批量存貯模型）
該模型滿足以下條件：
（1）短缺費為無窮，即 ?= ∞ ；
（2）當存貯降到零后，可以立即得到補充；
（3）需求是連續的、均勻的，即需求速度（單位時間的需求量） D 為常數；
（4）每次的訂貨量不變，訂購費不變；
（5）單位存貯費為 ?。
例：某商品單位成本為5元，每天保管費為成本的0.1%，每次定購費為10元。已知對該商品的需求是100 件/天，不允許缺貨。假設該商品的進貨可以隨時實現。問應怎樣組織進貨，才能最經濟。
model:
sets:
times/1 2/:n,Q,C;
endsets
data:
n=57 58;
enddata
C_D=10;
D=100*365;
C_P=0.005*365;
@for(times:n=D/Q;C=0.5*C_P*Q+C_D*D/Q);
end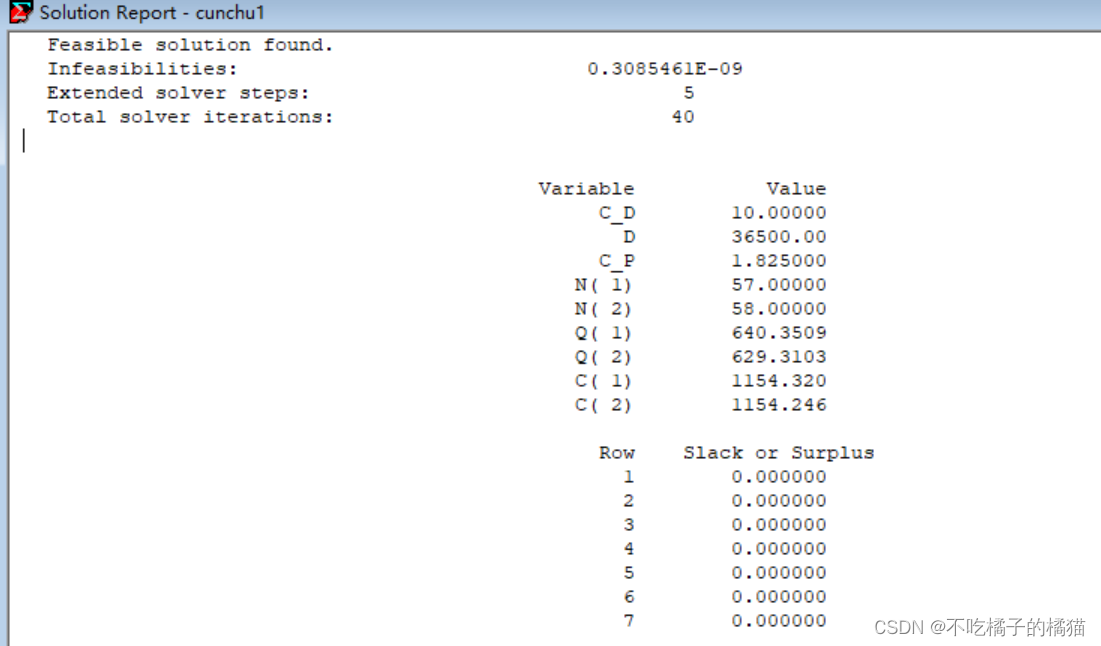
求整數解：
model:
sets:
times/1..100/:C,Q; !100不是必須的，通常取一個適當大的數就可以了;
endsets
C_D=10;
D=100*365;
C_P=0.005*365;
@for(times(i):Q(i)=D/i;C(i)=0.5*C_P*Q+C_D*D/Q);
C_min=@min(times:C);
Q_best=@sum(times(i):Q(i)*(C(i) #eq# C_min));
!(C(i) #eq# C_min)返回的值為0或1;
N_best=D/Q_best;
end 
?
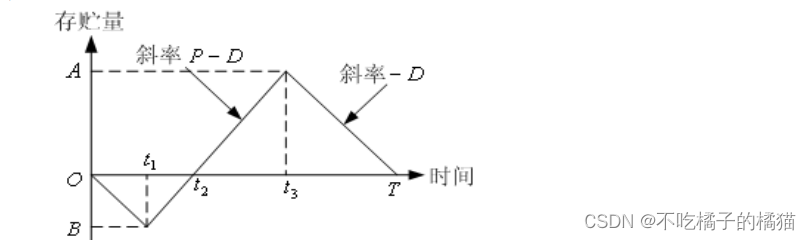
模型二：允許缺貨，補充時間較長(經濟生產批量存貯模型)
該模型滿足以下條件：
（1）需求是連續的，即需求速度（單位時間的需求量） D 為常數；
（2）補充需要一定時間。即一旦需要，生產可立刻開始，但生產需要一定周期。
設生產是連續均勻的，即生產速度 P 為常數。同時，設 P > D ；
（3）單位存貯費為 ?，單位缺貨費為 ，訂購費為 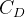。不考慮貨物價值。
例：有一個生產和銷售圖書設備的公司，經營一種圖書專用設備，基于以往的銷售記錄和今后市場預測。估計今后一年的需求量為4900個，由于占用資金的利息以及存貯庫房和其它人力物力的費用，存貯一個書架一年要花費1000元。這種書架是該公 司自己生產的，每年的生產量9800個，而組織一次生產要花費設備調試等生產準備費500元。如果允許缺貨，缺貨費為每年每件2000元。該公司為了把成本降到最低，應如何組織生產？要求出其生產、存貯周期，每個周期的最優生產量，以及最少的年總費用。
model:
D=4900;
C_P=1000;
P=9800;
C_D=500;
C_S=2000;
T=(2*C_D*(C_P+C_S)/(D*C_P*C_S*(1-D/P)))^0.5; !單位為年;
TT=T*365; !單位為天;
Q=D*T;
T_S=C_P*TT/(C_P+C_S); !求缺貨時間;
T_P=D*TT/P; ! 求生產周期;
C=2*C_D/T; ! 求年總費用;
end求得每個周期為 9 天，其中 9 天中有 4.5 天在生產，每次的生產量為 121 件，而且缺貨的時間有 3 天。總的費用（包括存貯費、訂貨費和缺貨費）為 40414.52 元。
模型三：不允許缺貨，補充時間較長(基本的經濟生產批量存貯模型)
在模型二的假設條件中，取消允許缺貨條件（即設 → ∞ ， t2 = 0 ），就成為模
型三。因此，模型三的存貯狀態圖和最優存貯策略可以從模型二直接導出。
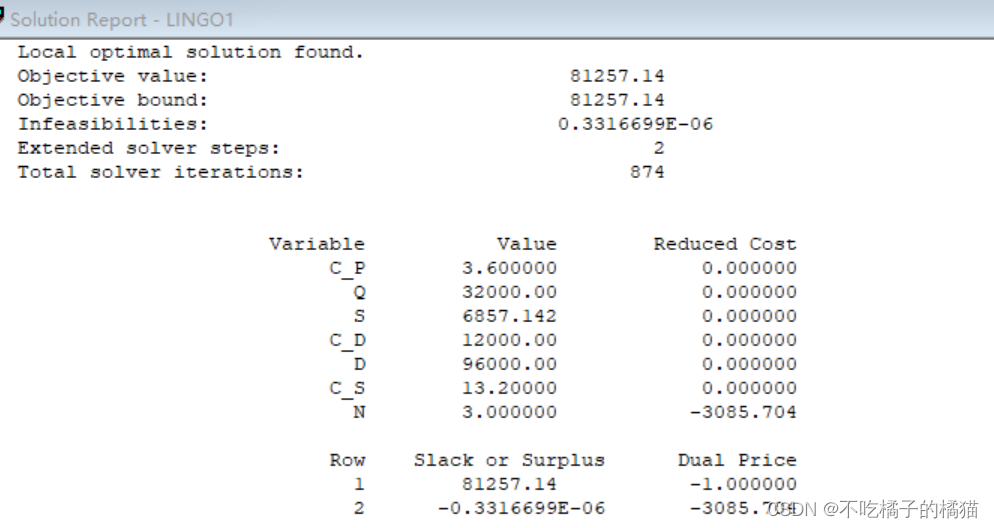
例：某電器公司的生產流水線需要某種零件，該零件需要靠訂貨得到。已知批量訂貨的訂貨費 12000 元/次，每個零件的存貯機費用為0.3元/（件·月），每個零件的缺貨損失為1.1 元/（件·月），設該零件的每月需求量為8000件。求全年的訂貨次數、訂貨量以及最優存貯費用。
model:
min=0.5*C_P*(Q-S)^2/Q+C_D*D/Q+0.5*C_S*S^2/Q;
n=D/Q;@gin(n);
data:
C_D=12000;
D=96000;
C_P=3.6;
C_S=13.2;
enddata
end得全年組織 3 次訂貨，每次的訂貨量為 32000 件，最大缺貨量為 6857.141 件， 最優費用為 81257.14 元
?
)
