機器人運動軌跡學習——GMM/GMR算法
-
前置知識
GMM的英文全稱為:
Gaussian mixture model,即高斯混合模型,也就是說,它是由多個高斯模型進行混合的結果:當然,這里的混合是帶有權重概念的。-
一維高斯分布
GMM中的個體就是高斯模型,說認真點就是高斯基函數,它還有另一個名字,徑向基函數。
對于一維變量,其高斯分布為:
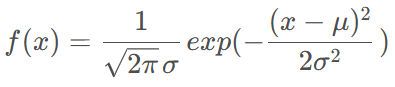
對應高斯概率密度的圖形:
也就是說,對于一維變量x,它落在均值區間 [ u ? σ , u + σ ] [u-\sigma, u+\sigma] [u?σ,u+σ]的概率為68.26%
-
多維高斯分布
多維 Gaussian 分布的概率密度函數為:
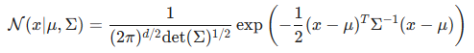
其中 μ \mu μ為均值向量, Σ \Sigma Σ為協方差矩陣
-
-
GMM對復雜軌跡的擬合
一個復雜運動的表達式可由一系列簡單信號的加權組合表述,我們稱這些簡單信號為基函數;
一些流行的基函數有:
Radial Basis Functions (RBFs),Bernstein Basis Functions,Fourier Basis Functions其中,
Radial Basis Functions (RBFs),即徑向基函數,一種應用如下圖所示:通過為各基函數賦予不同的權重,生成了一條相對復雜的軌跡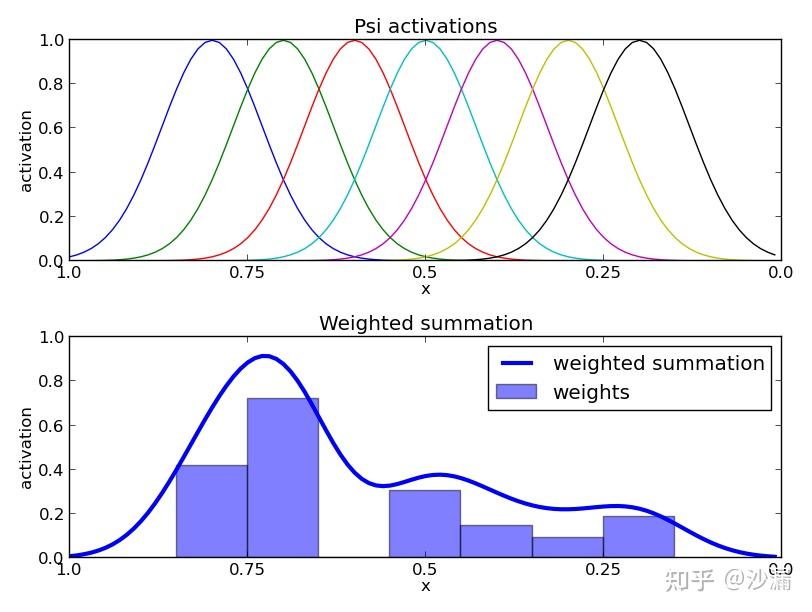
圖片源自:Dynamic Movement Primitives介紹及Python實現與UR5機械臂仿真 - 知乎 (zhihu.com)
-
GMR的回歸思想
GMR(
Gaussian mixture regression)的思想:對于一個輸入,借用GMM進行回歸,回歸的結果是一個高斯分布,
也就是說,我們回歸得到的結果不是一個固定的值,而是一個概率值
以一維高斯分布為例:

我們回歸得到的結果其均值為 μ \mu μ,在 [ u ? σ , u + σ ] [u-\sigma, u+\sigma] [u?σ,u+σ]區間內的概率為68.26%
而且回歸得到的這個高斯分布一般不是高斯混合分布中的某一個分布,而是一個新的分布
-
GMM的學習思想
根據我們的假設,GMM由多個高斯分布加權得到,那么GMM的概率密度函數為:
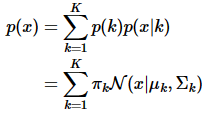
其中 p ( k ) = π k p(k)=\pi_k p(k)=πk?是取第 k k k個高斯核的概率, p ( x ∣ k ) = N ( x ∣ u k , Σ k ) p(x|k)=N(x|u_k,\Sigma_k) p(x∣k)=N(x∣uk?,Σk?)是在第 k k k個高斯核下,取值x的概率
x可以是一個向量
因此,如果我們要從 GMM 的分布中隨機地取一個點的話,實際上可以分為兩步:
- 首先隨機地在這 𝐾 個 高斯 之中選一個,每個 高斯 被選中的概率實際上就是它的系數 π k \pi_k πk? ,
- 選中了 高斯 之后,再單獨地考慮從這個 高斯 的分布中選取一個點就可以了
觀察概率密度函數的形式,我們需要確定的參數為 π k , μ k , Σ k \pi_k,\mu_k,\Sigma_k πk?,μk?,Σk?
已知(假定)了概率密度函數的形式,而要估計其中的參數的過程被稱作“參數估計”
-
GMM參數估計
-
思想
假設我們有一組數據點,假設他們服從分布p(x)(GMM中的一個高斯分布),我們要求其中的參數,
方法是直接假設一組參數,在這組參數( π k , μ k , Σ k \pi_k,\mu_k,\Sigma_k πk?,μk?,Σk?)下所確定的概率分布生成這組數據點的概率 π k \pi_k πk?最大
即EM算法的思想
-
步驟一(E步,后驗概率)
計算數據由每個高斯生成的概率:
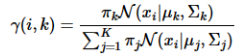
其中, π k , μ k , Σ k \pi_k,\mu_k,\Sigma_k πk?,μk?,Σk?取上一次迭代的值(或初始值)
-
步驟二(M步,估計相關的參數)
調整參數
對上面的公式進行對數似然,有:
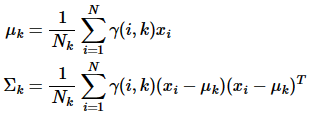
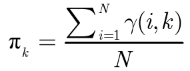
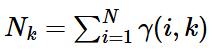 N是數據點的個數
N是數據點的個數 -
步驟三
重復上述步驟,直到滿足我們的收斂條件(概率密度函數幾乎不變)或超過設定的最大迭代次數
-
補充
我們注意到,在第一次執行上述步驟一時,參數 π k , μ k , Σ k \pi_k,\mu_k,\Sigma_k πk?,μk?,Σk?未知,這時我們需要給定一組初值,初值的好壞對收斂有影響,詳情可參考漫談 Clustering (3): Gaussian Mixture Model (pluskid.org)。
-
-
GMR參數回歸
完成GMM模型的建立后,得到高斯混合模型:
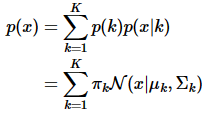
為了對給定參數進行回歸,我們對其中的參數x,將其分為輸入參數及輸出參數,即有:
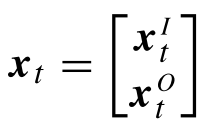
其中下標
t表示輸入變量是t,輸出變量可以是
t對應的二維坐標(x1,x2)根據GMR回歸思想,對于均值和協方差,自然就分為:
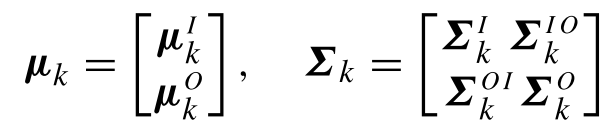
于是,直接根據公式,輸入對單個高斯的回歸,有:
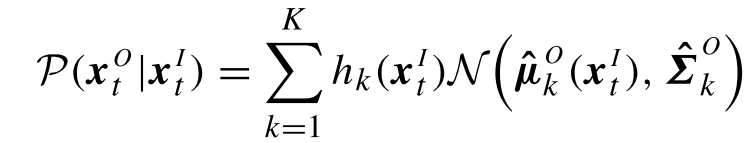
其中:
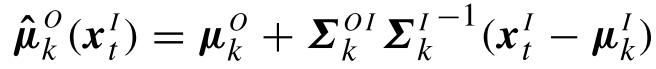
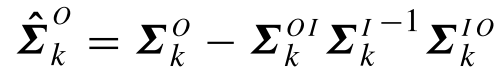
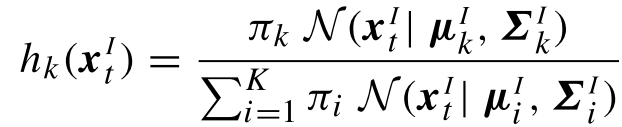
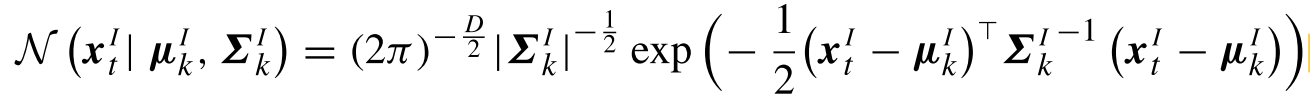
對于最終的結果,有:
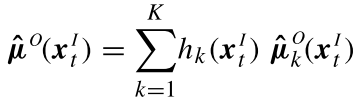
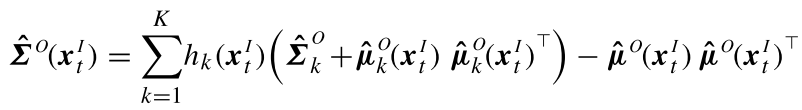










)








