通過前幾期的學習，我們已經學會了排隊論的基本概念、生滅過程和Poisson過程，等待制排隊模型、混合制排隊模型、其他排隊模型以及排隊系統優的定義與相關求解方法。在實際工作中，我們能發現排隊論在經濟管理中有著許多應用，本期小編選擇了其中一些典型例子，包括等待制排隊模型、混合制排隊模型以及M/M/1模型中的最優服務率問題，進行詳細講解。

一些常見的等待制模型包括：M/M/1單服務臺等待制模型：一個服務臺，到達和服務時間都是指數分布；M/M/s多服務臺模型：多個服務臺，到達和服務時間都是指數分布。這些模型可以用于計算系統的性能指標，如平均等待時間、系統繁忙度、平均服務時間等。通過分析這些指標，可以優化系統，提高效率，降低等待時間，從而提升顧客體驗。

1、問題描述

工廠中只有一個服務臺，工件按泊松流到達服務臺，平均間隔時間為10分鐘，假設對每一工件的服務所需時間服從負指數分布，平均服務時間8分鐘。求:

（1）工件在系統內等待服務的平均數和工件在系統內平均逗留時間；

（2）若要求在90%的把握使工件在系統內的逗留時間不超過30分鐘，則工件的平均服務時間最多是多少；

（3）若每一工件的服務分兩段，每段所需時間都服從負指數分布，平均都為4分鐘，在這種情況下，工件在系統內的平均數是多少?

2、問題解析

由題目可知該問題是M/M/1單服務臺等待制模型，其中到達率λ=1/10，服務率μ=1/8，服務強度ρ=0.8。

（1）工件在系統內等待服務的平均數即排隊長

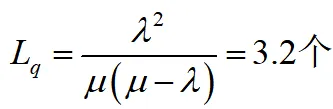
工件在系統中的平均逗留時間

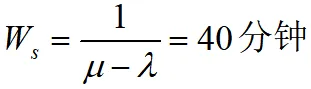
（2）工件在系統中逗留時間不超過30分鐘的概率

得

故工件得平均服務時間最多為5.6分鐘。

（3）此時模型變為M/M/2等待制排隊模型，其中s=2服務率μ1=μ2=0.25=μ，服務強度ρ=λ/μ=0.4，ρs=λ/2μ=0.2，則平均排隊長

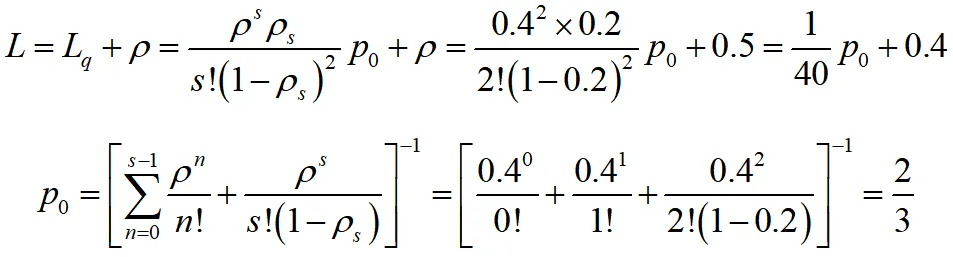
故系統中的工件數為

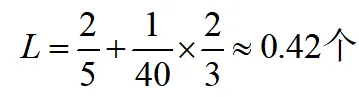
小結

單服務臺模型與多服務臺模型的區別：

（1）服務臺數量：

單服務臺模型：只有一個服務臺為顧客提供服務

多服務臺模型：包含多個服務臺，每個服務臺都可以同時為顧客提供服務

（2）服務率：

單服務臺模型：取決于單個服務臺的處理能力

多服務臺模型： 由所有服務臺的總體處理能力決定，取決于每個服務臺的速率以及服務臺的數量

在現實生活中，很多服務系統都應用混合制排隊模型，當顧客到達時，服務臺不空就排隊，若排隊位置已滿就離去，如果系統的最大容量為K ，對于單服務臺的情形，排隊等待的顧客最多為K-1，在某時刻，顧客到達時，如系統中已有K個顧客，那么這個顧客就被拒絕進入系統。

1、問題描述

單人理發館有 6 個椅子接待人們排隊等待理發。當 6個椅子都坐滿時，后來到的顧客不進店就離開。顧客平均到達率為 3人/小時，理發平均每人15 分鐘。

（1）求某顧客到達理發館就能理發的概率；

（2）求需要等待的顧客數的期望值；

（3）求有效到達率；

（4）求顧客在理發館內逗留的期望時間；

（5）在可能到來的顧客中不等待就離開的概率。

2、問題解析

根據題目可知，該問題是該模型為K=7的M/M/1/K的模型，可得到達率λ=3人/小時，服務率μ=4人/小時，服務強度ρ=λ/μ=0.75

（1）到達理發館就能理發情形相當于理發館內沒有顧客，所求概率

（2）需要等待的顧客數的期望值，就是平均排隊長

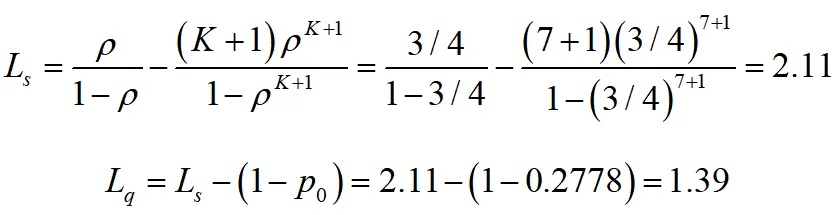
（3）顧客的有效到達率為

（4）顧客在理發館內逗留的期望時間就是平均逗留時間

（5）顧客不等待就離開的概率，即系統拒絕率也是系統滿員率

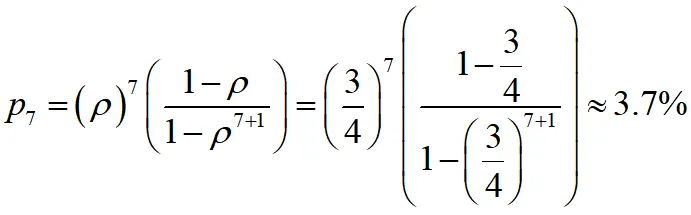
這也是理發館的損失率為3.7%。

總結

等待制模型與混合制模型的區別

等待制模型：顧客源無限，系統空間無限，允許無限排隊，當顧客到達時所有的服務臺均被占用，顧客就排隊等待，直到接受完服務才離去。

混合制模型：顧客源無限，系統空間有限，不允許無限排隊，混合制模型既有等待又有損失，在限度以內就排隊等待，超過一定限度就離去。

在M/M/1隊列模型中，最優服務率通常是指能夠使系統達到某種性能指標的最佳服務率。這個性能指標可能是最小的平均等待時間、最小的系統繁忙度或最大的系統通過率。具體來說，M/M/1模型的最優服務率是在給定到達率的情況下，通過調整服務率μ來實現某個優化目標。

1、問題描述

某公司醫務室為職工檢查身體，職工的到達服從泊松分布，每小時平均到達50人，若職工不能按時體檢，造成的損失為每小時每人平均60元。體檢所花時間服從指數分布負指數分布，平均每小時服務率為μ，每人的體檢費為30元，試確定使公司總支出最少的參數μ。

2、問題解析

該問題求解公司總支出最少的參數μ，即平均服務率的最優值，根據題意可知，該排隊模型為M/M/1模型，那么單位時間服務成本與顧客在系統逗留費用之和

式中Cs為當μ=1時服務機構單位時間的費用；Cw為每個顧客在系統停留單位時間的費用。則代入模型的平均隊長公式可得

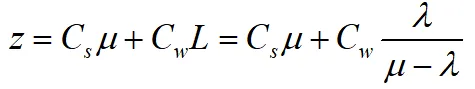
對μ進行求導，并令導數為零，得

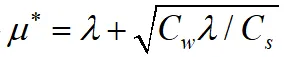
故

注意

? ? ? ?M/M/1模型是相對簡單的排隊模型，因此最優服務率的解通常可以通過解析方法找到，對于更復雜的排隊模型，可能需要使用數值方法進行求解。

? ? ? ?以上就是本期排隊論例題講解的全部內容啦，通過對這一期的學習，相信大家一定能夠加深對排隊論的理解，進而在生活實踐中學會應用！

作者 | 林鑫?馬書良

責編 | 王一靜

審核 | 徐小峰