本節課我們介紹信道極限容量的有關問題。
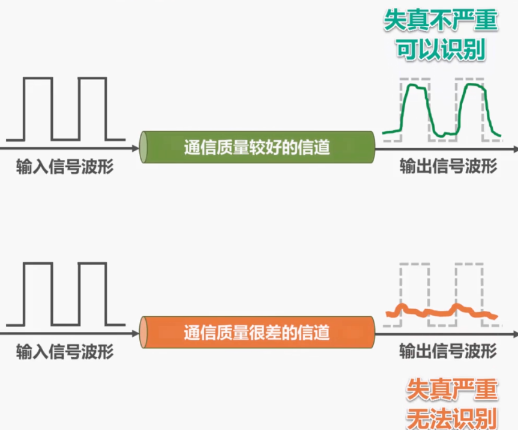
我們都知道信號在傳輸過程中會受到各種因素的影響,如圖所示,這是一個數字信號,??當它通過實際的信道后,波形會產生失真,當失真不嚴重時,在輸出端??還可根據以失真的波形還原出發送的碼元,但當失真嚴重時,在輸出端??就很難判斷這個信號??在什么時候是 1 和在什么時候是 0。
信號波形失去了碼元之間的清晰界限,??這種現象叫做碼間串擾。??
? ?
?
?
產生失真的原因主要有碼元傳輸速率、信號傳輸距離、??噪聲干擾,傳輸媒體質量等。
?
奈氏準則
早在 1924 年,奈奎斯特就推導出了著名的奈氏準則,??他給出了在假定的理想條件下,為了避免碼間串擾,碼元傳輸速率的上限。
理想低通信道的最高碼元傳輸率等于 2W 波特,理想帶通信道的最高,碼元傳輸速率等于 W 波特,??這里的 W 是信道帶寬,單位為赫茲,單詞 Baud 的意思是波特,也就是碼元每秒,因此上述公式可進一步寫為 2w 碼元/秒 和 w 碼元/秒:
? ?
?
?
碼元傳輸速率又稱為波特率,調制速率,波形速率??或符號速率,它與比特率有一定的關系。??
當一個碼元只攜帶一比特的信息量時,波特率,??也就是單位為碼元每秒與比特率也就是單位為比特每秒,在數值上是相等的。??
當一個碼元攜帶 n 比特的信息量時,則波特率轉換成比特率時,數值要乘以 n??
?
要提高信息的傳輸速率,就必須設法使每一個碼元能夠攜帶更多個比特的信息量,??這需要采用多元制。??
還記得我們上節課中介紹的調幅、調頻以及調向這三種基本調制方法嗎???它們屬于二元調制,只能產生兩種不同的碼元,也就是兩種不同的基本波形。??因此??每個碼元只能攜帶一比特的信息量。
而混合調制屬于多元調制。例如?? QAM16 可以調制出 16 種不同的碼元,因此每個碼元可以攜帶 4 比特的信息量。
?
需要說明的是??實際的信道所能傳輸的最高碼元速率要明顯低于奈式準則給出的上限值,??這是因為奈式準則是在假定的理想條件下推導出來的,他不考慮其他因素,例如傳輸距離、??噪聲干擾,傳輸媒體質量等。
僅從公式來看,只要采用更好的調制方法,??讓碼元可以攜帶更多的比特,豈不是可以無限制的提高信息的傳輸速率嗎?答案是否定的,??信道的極限信息傳輸速率還要受限于實際的信號,在信道中傳輸時的信噪比,??因為信道中的噪聲也會影響接收端對碼元的識別,并且噪聲功率相對信號功率越大,??影響就越大。??
香農公式
1948 年香農用信息論的理論推導出了帶寬受限,??且有高斯白噪聲干擾的信道的極限信息傳輸速率,具體公式如下所示。其中?? c 是信道的極限信息傳輸速率,單位是比特每秒,w 是信道帶寬,單位為赫茲,??s 是信道內所傳送信號的平均功率,n 是信道內的高斯噪聲功率,s 比 n 是信噪比??使用分貝作為度量單位如下所示。??
從香農公式可以看出,信道帶寬或信道中信噪比越大,信息的極限傳輸速率就越大。
需要說明的是在實際信道上能夠達到的信息傳輸速率,要比該公式的極限傳輸速率低不少,??這是因為在實際信道中信號還要受到其他一些損傷,例如各種脈沖干擾,??信號在傳輸中的衰減和失真等,這些因素在香農公式中并未考慮。??
? ?
?
?
綜合來看奈式準則和香農公式。在信道帶寬一定的情況下,要想提高信息的傳輸速率,??就必須采用多元制,??并努力提高信道中的信噪比。
自從香農公式發表以后,各種新的信號處理和調制方法??就要不斷出現,其目的都是為了盡可能的接近香農公式所給出的傳輸速率極限。??
?
?
習題
接下來??我們來做幾個與這兩個公式有關的練習題。
這是計算機專業考研全國統考計算機網絡部分??2014 年的題 35,答案是 D。
從香農公式可知,信噪比和頻率帶寬都會影響信道數據傳輸速率。??從奈式準則可知,??調制速度也就是碼元傳輸速度和碼元所攜帶的比特數量,都會影響信道數據傳輸速率,??而信號的傳播速度不影響數據傳輸速率。??我們在之前的課程中??曾建議同學們記住電磁波在不同傳輸媒體的傳播速率,不知大家是否還記得。??
? ?
?
?
來看 2009 年的題 34,在無噪聲的情況下,若某通信鏈路帶寬為 3000 赫茲,??采用 4 個相位,每個相位具有 4 種振幅的 QAM 調制技術,??則該通信鏈路的最大數據全速率是多少?我們一起來做這道題:
一,根據奈式準則可知,??該通信鏈路的最高碼元傳送率 = 2×3k = 6k 波特,也就是 6k 碼元每秒。??
二,采用 4 個相位,每個相位 4 種振幅的 qam 調制技術,可以調制出 16 個不同的基本模型,??也就是 16 個不同的碼元,采用二進制對這 16 個不同的碼源進行編碼,??需要使用 4 個比特。??換句話說,每個碼元可以攜帶的信息量為 4 比特。
綜合 1 和 2 可知,??該通信鏈路的最大數據傳送率等于 6k 碼元每秒 ×4 比特每碼元?? = 等于 24k 比特每秒,也就是 24kbps
? ?
?
?
因此本題的正確答案是選項 B。實際上對于這種類型的題目,不管題目給出的調制技術多么牛,或者對于我們而言多么陌生,??這都不會影響我們解題。??我們只需關心這種調制技術,可以調制出多少個不同的基本波形即可。
?
?
?
?
來看 2011 年的題目 34,??答案是選項 B,我們來看解題過程:
一,采用四相位調制,可以調制出 4 種相位不同的基本波型,??采用二進制對這 4 種不同的波形進行編碼,需要使用兩個比特。換句話說,??每個碼元可以攜帶的信息量為兩個比特。??
二,數據傳送速率等于波特率,也就是碼元傳輸速率 乘以?? 每個碼元所攜帶的信息量。帶入本題的相關數值,也就是 2400 比特每秒,等于波特率??乘以 2 比特美碼元,解得波特率等于 1200 馬元每秒,也就是 1200 波特。??
? ?
?
?
?
再來看 2016 年的題 34,若連接 R2 和 R3 鏈路的頻率帶寬為 8000 赫茲,??性噪比為 30 分貝,該鏈路實際數據傳輸速率約為理論最大數據傳輸速率的 50%,??則該鏈路的實際數據傳輸速率約是多少?
根據香農公式可知,??本題中的理論最大數據傳送率為 8000 赫茲,乘以 log 以 2 為底,1+ 信噪比的對數,??信噪比采用分貝表示,題目所給信噪比為 30 分貝,可計算出信噪比為 1000,代入上式,??可計算出結果約等于 80kbps。根據提議,??該鏈路的實際數據傳輸率是理論值的 50%,計算結果為 40kbps??,因此選項 C 正確。??
? ?
?
?
再來看 2017 年的題 35,答案是選項 D。
設信號狀態數,??也就是可調制出的不同基本波形或碼元數量為 x,則每個碼元可攜帶的比特數量為?? log 以 2 為底 x 的對數。??信道在無噪聲情況下的極限數據傳輸速率,用奈式準則來計算,??等于 2w 碼元每秒,等于 2w log 以 2 為底 x 的對數比特每秒。??信道在無噪聲情況下的極限數據傳輸速率,用香農公式來計算,等于?? w 乘以 log 以 2 為底,1+1000 的對數,單位為比特每秒,其中的 1000??是 30 分貝信噪比換算出來的比值,根據題意列出不等式,解得?? x 大于等于 32。
? ?
?
?
本節課到這里就結束了。??在本節課中,我們介紹了與信道極限容量相關的兩個公式,一個是奈式準則,??另一個是香農公式。他們為提高信息傳輸速率提供了理論依據,希望同學們能夠掌握??并利用這兩個公式進行一些簡單的相關計算。
?
?
?
物理層習題
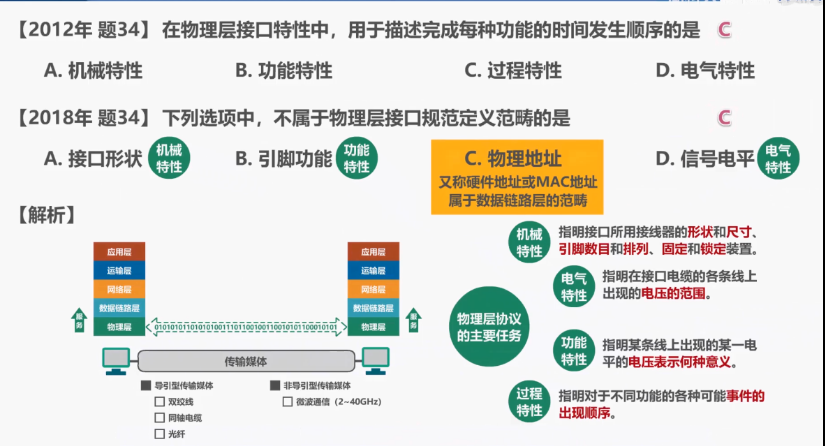
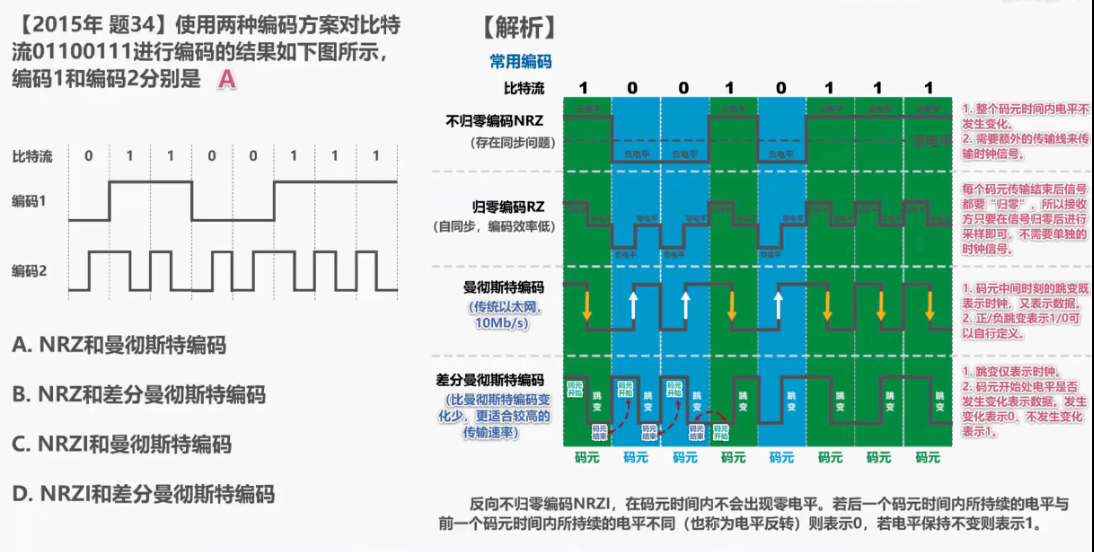
來看幾道考研題:
? ?
?
?
? ?
?
?
?



















:窗口看門狗(WWDG)實驗)