目錄

1.程序功能描述

2.測試軟件版本以及運行結果展示

3.核心程序

4.本算法原理

5.完整程序

---

1.程序功能描述

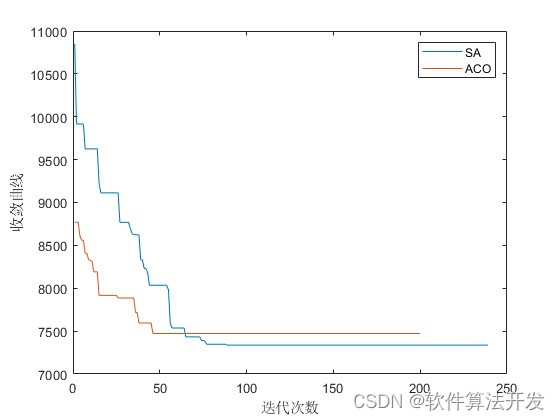
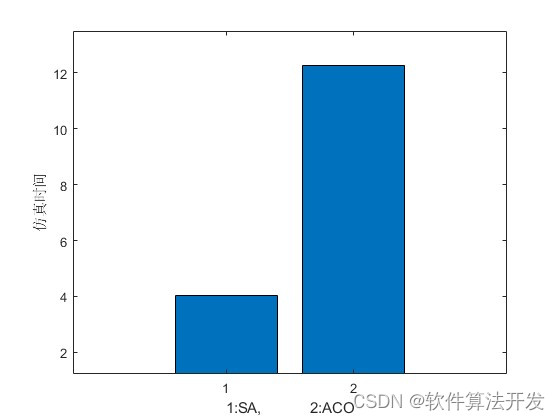
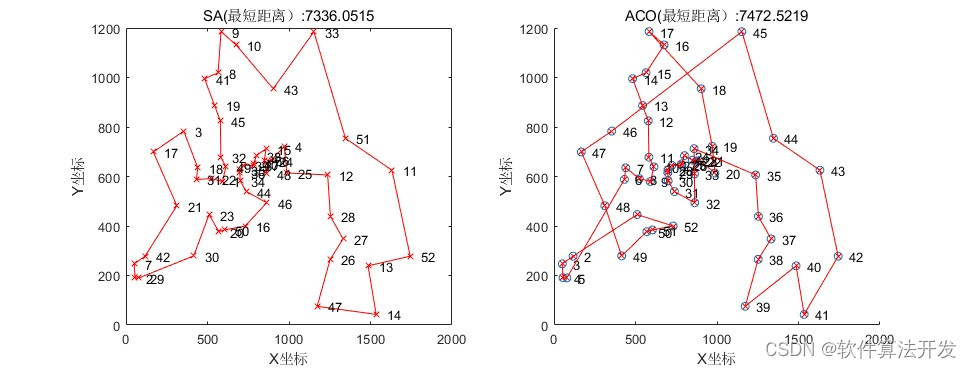
? ? ? ?基于SA模擬退火優化算法的TSP問題求解matlab仿真,并對比ACO蟻群優化算法,對比兩個算法的仿真時間，收斂曲線，以及路徑規劃的結果，最短路徑長度。

2.測試軟件版本以及運行結果展示

MATLAB2022A版本運行

3.核心程序

...........................................................................
while t>=Temp1%溫度降溫判決tfor j=1:MK_lineif rand<0.75%交換順序idx1=0;idx2=0;while(idx1==idx2&&idx1>=idx2)idx1=ceil(rand*n);idx2=ceil(rand*n);end                      Rout_tmp    = Rout1(idx1);Rout1(idx1) = Rout1(idx2);Rout1(idx2) = Rout_tmp;elseidx0   = zeros(3,1);Lidx   = length(unique(idx0));while Lidx<3 idx0 = ceil([rand*n rand*n rand*n]);Lidx = length(unique(idx0));endStidx0 = sort(idx0);Stidx1 = Stidx0(1);Stidx2 = Stidx0(2);Stidx3 = Stidx0(3);route0 = Rout1;route0(Stidx1:Stidx1+Stidx3-Stidx2-1) = Rout1(Stidx2+1:Stidx3);route0(Stidx1+Stidx3-Stidx2:Stidx3)   = Rout1(Stidx1:Stidx2);Rout1                                 = route0;    end %計算路徑的距離 Lent = 0;Route= [Rout1 Rout1(1)];for j = 1:nLent = Lent + md(Route(j),Route(j + 1));end
endfigure;
plot(Tempset);
xlabel('迭代次數');
ylabel('模擬退火收斂曲線');%結果顯示 
time = toc;figure;
Route=[Routb Routb(1)];
plot([Pxy(Route ,1)], [Pxy(Route ,2)],'r-x');
for i = 1:n%對每個城市進行標號text(Pxy(i,1),Pxy(i,2),['   ' num2str(i)]);
end
xlabel('X坐標')
ylabel('Y坐標')
title(['SA(最短距離）:' num2str(Lbest) ''])save R1.mat Tempset time Lbest Routb Route Pxy n
54

4.本算法原理

? ? ? ? 旅行商問題（Traveling Salesman Problem, TSP）是一個經典的組合優化問題，目標是尋找最短的可能路線，使得旅行商能夠訪問每個城市恰好一次并最終返回出發點。模擬退火算法（Simulated Annealing, SA）和蟻群優化算法（Ant Colony Optimization, ACO）是解決此類問題的兩種啟發式優化方法，它們各自以不同的自然現象為靈感，展示了優化問題的生物啟發式解決方案。

? ? ? ?模擬退火算法源于金屬熱處理中的退火過程，通過模擬固體冷卻過程中的微觀狀態轉變來搜索全局最優解。它允許算法在搜索過程中暫時接受比當前解更差的解，從而有助于跳出局部最優，達到全局探索。

? ? ? ?蟻群優化算法模仿螞蟻在尋找食物過程中留下信息素痕跡的行為，通過正反饋機制來發現最短路徑。

對比分析

• 探索與利用平衡：SA通過溫度參數控制探索與利用的平衡，高溫時更傾向于探索全局，低溫時偏向于局部精煉；而ACO通過信息素濃度和啟發式信息調節，信息素濃度高的路徑更容易被再次選擇，同時信息素揮發機制促進探索。

• 全局優化能力：SA理論上能較好地跳出局部最優，但在參數設置不當（如冷卻速率過快或過慢）時，可能影響性能；ACO通過正反饋機制和分布式搜索，也表現出較好的全局尋優能力，但依賴于參數調優和初始化。

• 計算復雜度：SA的計算復雜度相對較低，主要在于狀態轉移和接受準則的計算；ACO在大規模問題中可能面臨較高的計算復雜度，尤其是信息素更新和選擇概率的計算。

• 適用性：SA因其靈活性和通用性，適合于多種類型的優化問題；ACO則特別適合解決路徑優化類問題，其生物學背景使其在理解和解釋上更為直觀。

5.完整程序

VVV