題目描述

• 給定一個按照升序排列的長度為n的整數數組，以及q個查詢。
• 對于每個查詢，返回一個元素k的起始位置和終止位置（位置從0開始計數）。
• 如果數組中不存在該元素，則返回 -1 -1。

輸入格式：

• 第一行包含整數n和q，表示數組長度和詢問個數。
• 第二行包含n個整數（均在1～10000范圍內），表示完整數組。
• 接下來q行，每行包含一個整數k，表示一個詢問元素。

輸出格式：

• 共q行，每行包含兩個整數，表示所求元素的起始位置和終止位置。
• 如果數組中不存在該元素，則返回 -1 -1。

題目思路

• 本題實際上是一個整數二分問題，相當于從一個有序數組中找到兩個邊界，正好可以用二分查找方法進行解決。
• 首先，需要找到左邊界，即指定的查詢數字在數組中的最靠前的出現位置。因此，只需要以中點為參考，判斷中點是否滿足大于等于需要查詢的數值，然后分情況設置下一個區間即可。重復這種情況，直到左右端點重合，則返回此時的點。
  • 如果中點對應的值確實大于等于需要查詢的數值，則說明需要查詢的數值在以中點為劃分的左半邊區間內（這個區間包含了上一步的中點），因此將區間的右端點修改為當前的中心點。
  • 如果中點對應的值小于需要查詢的數值，則說明需要查詢的數值在以中點為劃分的右半區間內（這個區間不包含中點，因為中點的值小于查找的值），因此將區間的左端點設置為當前中心點右邊的第一個端點即可。

為什么判定條件是大于等于而不是小于等于：如果采用小于等于，則會將原始的有序數組劃分為大于等于查詢值和小于查詢值的兩部分，此時，每一次如果中點小于等于當前查詢的值，那么左端點可能在中點的右邊（即中點實際是小于查詢值的）或中點的左邊（查詢值有多個位置，中點并非最靠左的一個），因此無法繼續二分。

為什么判定條件不使用大于或小于：以大于為例，如果采用大于，則會將原始的有序數組劃分為大于查詢值和小于等于查詢值的兩部分。此時，每一次如果中點大于當前查詢的值，一定可以判定待查詢的值一定在左半邊區間內，但是如果中點小于等于查詢值，則無法判定左邊界的位置，因為左邊界可能在中點左邊（當中點等于查詢值，且不是排在最前面的時候）或中點右邊（中點小于查詢值時）。

• 如果此時返回的端點仍然不等于需要查找的值，說明原始數組中不存在和需要查找的值相等的元素，輸出 -1 -1；否則，繼續進行后續的步驟。
• 后續步驟即為找出區間的右端點。與找出左端點類似，但是將條件修改為判斷中點是否滿足小于等于需要查詢的數值。當中點小于等于需要查詢的數值的時候，說明其一定在以右邊界為軸點的左邊區間中，因此將區間的左端點設置為右邊界即可；當中點大于需要查詢的數值的時候，說明其一定在以右邊界為軸點（不包括右邊界）的右邊區間中，因此將區間的右端點設置為中點向左移動一個單位后的端點即可。

題目代碼（C++）

#include <cstdio>int n,q;
const int N(1e5 + 10);
int arr[N];
int query;int main(void)
{scanf("%d %d", &n, &q);for(int i(0); i < n; ++i) scanf("%d", &arr[i]);for(int i(0); i < q; ++i) {scanf("%d", &query);int left(0), right(n - 1);while(left < right){int mid((left + right) >> 1);if(arr[mid] >= query) right = mid;else left = mid + 1;}if(arr[left] != query) printf("-1 -1\n");else{printf("%d ",left);left = 0, right = n - 1;while(left < right){int mid((left + right + 1) >> 1);if(arr[mid] <= query) left = mid;else right = mid - 1;}printf("%d\n", right);}}return 0;
}

題目感想

• 整數二分算法的模板中，需要注意如果是滿足條件需要將左邊界修改為區間中點（即left = mid），則進行中點位置計算時需要額外加1，否則會出現死循環。
• 二分的最大難點在于判斷使用什么中點判定條件，如上代碼所示。
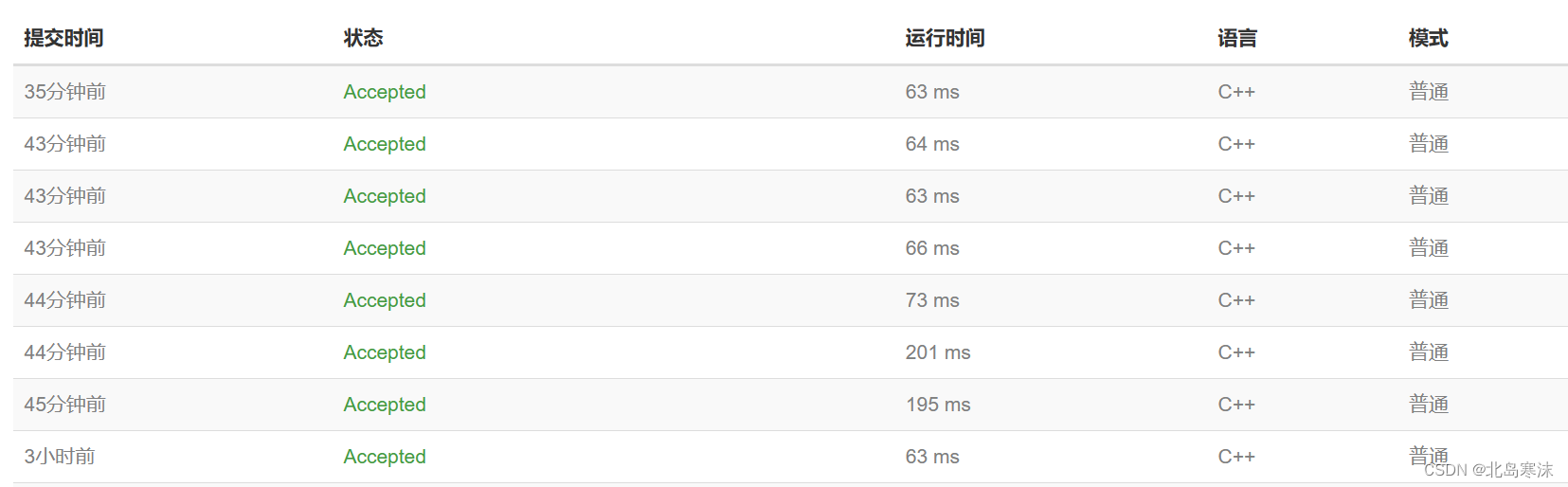
• 嘗試將代碼中的所有scanf函數修改為C++中的cin輸入方式，發現運行時間天差地別，如下圖所示。圖中所有兩位數的運行時間都是使用scanf得到的結果，三位數的運行時間都是cin得到的結果。